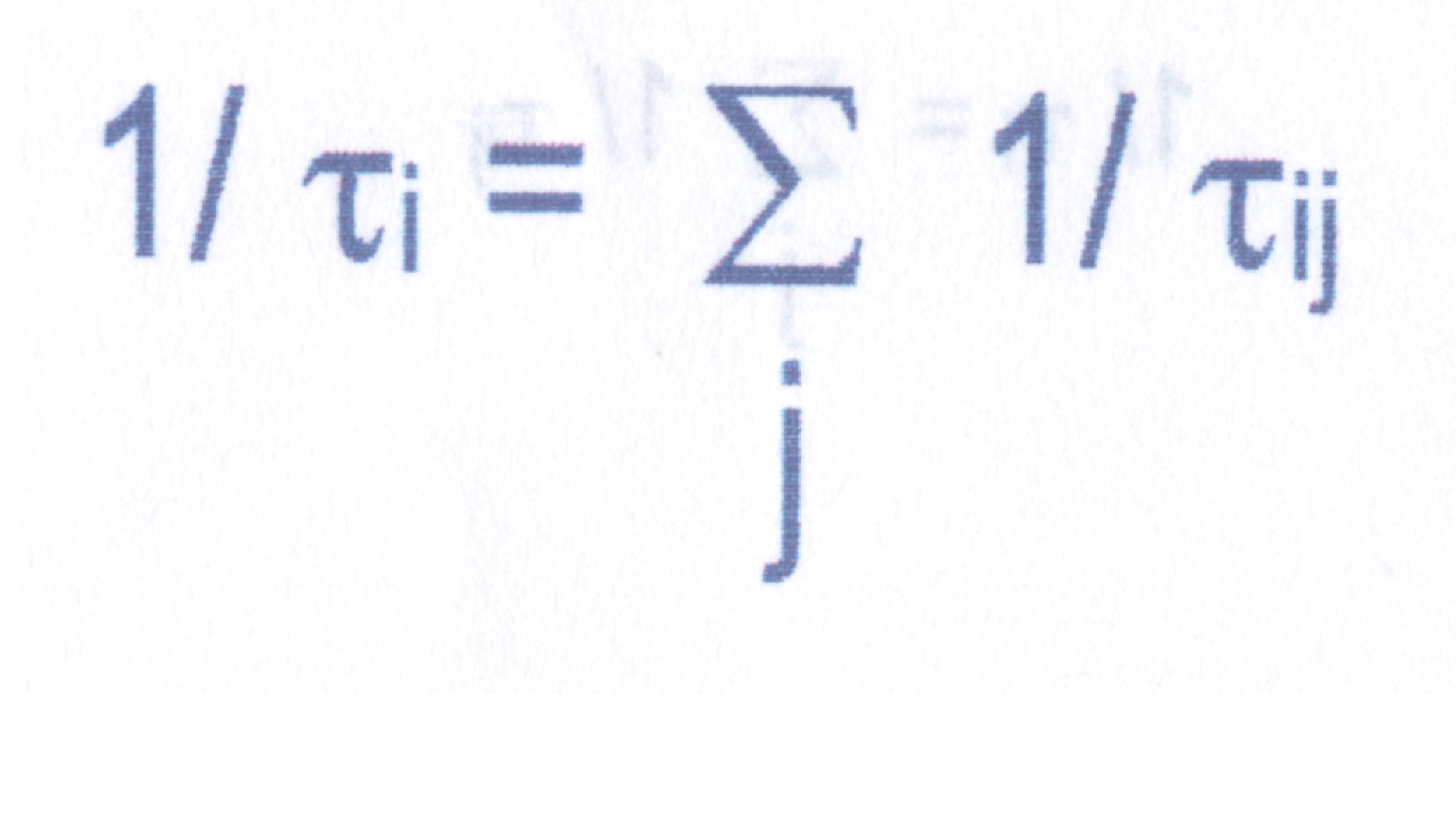
CHAPTER 2

How Lasers Work

2.1   Introduction

Laser oscillators produce highly coherent, monochromatic and highly directional electromagnetic radiation in the frequency range 10 ¹² – 10 ¹⁶ Hz (IR, Visible and UV). The gain in the laser oscillator is provided by atoms, ions, molecules and ‘free’ electrons while an optical resonator consisting of a pair of curved/plane/a combination of curved and plane mirrors provide the feedback. One of the resonator mirrors is 100% reflecting, while other mirror (output-coupler) is partially transmitting. Useful output from the laser is obtained through the output-coupler whose transmission depends on the gain of the medium. In case the medium can provide gain on more than one frequency, under same conditions, a dispersive element like a prism, a grating or a birefringent filter is incorporated in the optical resonator. The energy is to be supplied to the atoms/ions/molecules so that these exhibit a gain. This energy is provided by photons (optical pumping), electrical discharge (pulsed and DC), chemical reaction and thermodynamic techniques. In case of ‘free electrons’ the kinetic energy to the electrons is provided by an accelerator, while a non-uniform magnetic field helps in ‘lasing’ of the electrons. Thus main parts of a laser are:

1. Gain medium
2. Pump to create conditions so that the medium has gain
3. Optical resonator for feed back and tuning.

2.2   Gain Medium

Population of the energy levels associated with atoms/ions/molecules/ ’free electrons’ is manipulated so that these exhibit gain. Atoms/ions/molecules are characterized by a set of quantized energy levels while in case of 'free electrons' the associated energy levels are continuous. Atoms/ions/molecules have two distinct constituents (i) nucleus consisting of protons and neutrons and (ii) electrons moving in well-defined orbits surrounding the nucleus. Population of the electrons in these orbits provide the gain for the lasers. Normally only a few electronic energy levels have population and the highest energy level which has population under normal conditions of pressure, temperature and physical state of the atoms/ions/molecules, is called the ground state. All states (excited states) above the ground state do not have population ordinarily and one has to supply energy to populate the excited states. One of the ways of populating the excited states is by absorption of a photon of energy hn so that

E_i – E_g = hn

where

E_i = energy of 'i' excited state

E_g = energy of the ground state

h = Planks constant

n = frequency of the photon

This process, known as absorption is stimulated process that can happen only in presence of an electromagnetic field. Transition probability per unit time for absorption from ground level 'g' to the excited level 'i' is given by B_gi r (n ) where r (n ) is radiation density of the electromagnetic field characterized by the photons of energy hn . Once the excited level 'i' is populated it gets depopulated through the following processes:

(I) All the population in level 'i' make a transition to the ground state accompanied by the emission of a photon of frequency given by

hn = E_i - E_g

This is called spontaneous emission as no electromagnetic field is needed for this process. The transition probability for this transition is given by A_ig, Einistines A co-efficient. There could be a spontaneous transition for 'i' to 'j' , another excited level (E_i > E_j) , j to k ( E_j > E_k) and so on. However, finally the population ends in the ground state.

II) The level ‘i’ decays down to another excited level or to the ground level in presence of an electromagnetic field (stimulated transition) accompanied by the emission of the photon of energy hn = E_i – E_m where m = j, h, ----g. The transition probability for this stimulated transition is given by B_im r (n ) ( m = j,k, ------g) , where B_im is Einstein B co-efficient satisfying the relation B_im = B_mi & r (n ) is radiation field density. Not only is the frequency of the emitted photon same as that of radiation field but also the two are in phase so that the emitted photon increases the photon number of the radiation field, that is the radiation field gets amplified – quit opposite to absorption in which case the photon number of the radiation field decreases.

(3) The level ‘i’ is depopulated by decaying down to a lower state (excited or ground) without emission of a photon. This is called a radiationless transition and its transition probability depends not only on the nature of initial & find states involved in the transition but also on the factors like temperature, pressure etc. Depopulation through collisions in case of gases is an example of radiationless transitions. In case of solids the energy increases the temperature of the lattice (transition via phonons).

In general, a state can depopulate by a combination of radiative and non-radiative transitions to a number of lower levels. There are number of selection rules which determine whether a particular transition is allowed or not allowed. However, lack of complete knowledge about the nature of wavefunctions characterizing the states involved in a transition, makes these selection rules less rigorous. However, a quantity which characterizes each state and can be measured very accurately is the lifetime of a state. Lifetime t _i of state `i’ is defined as

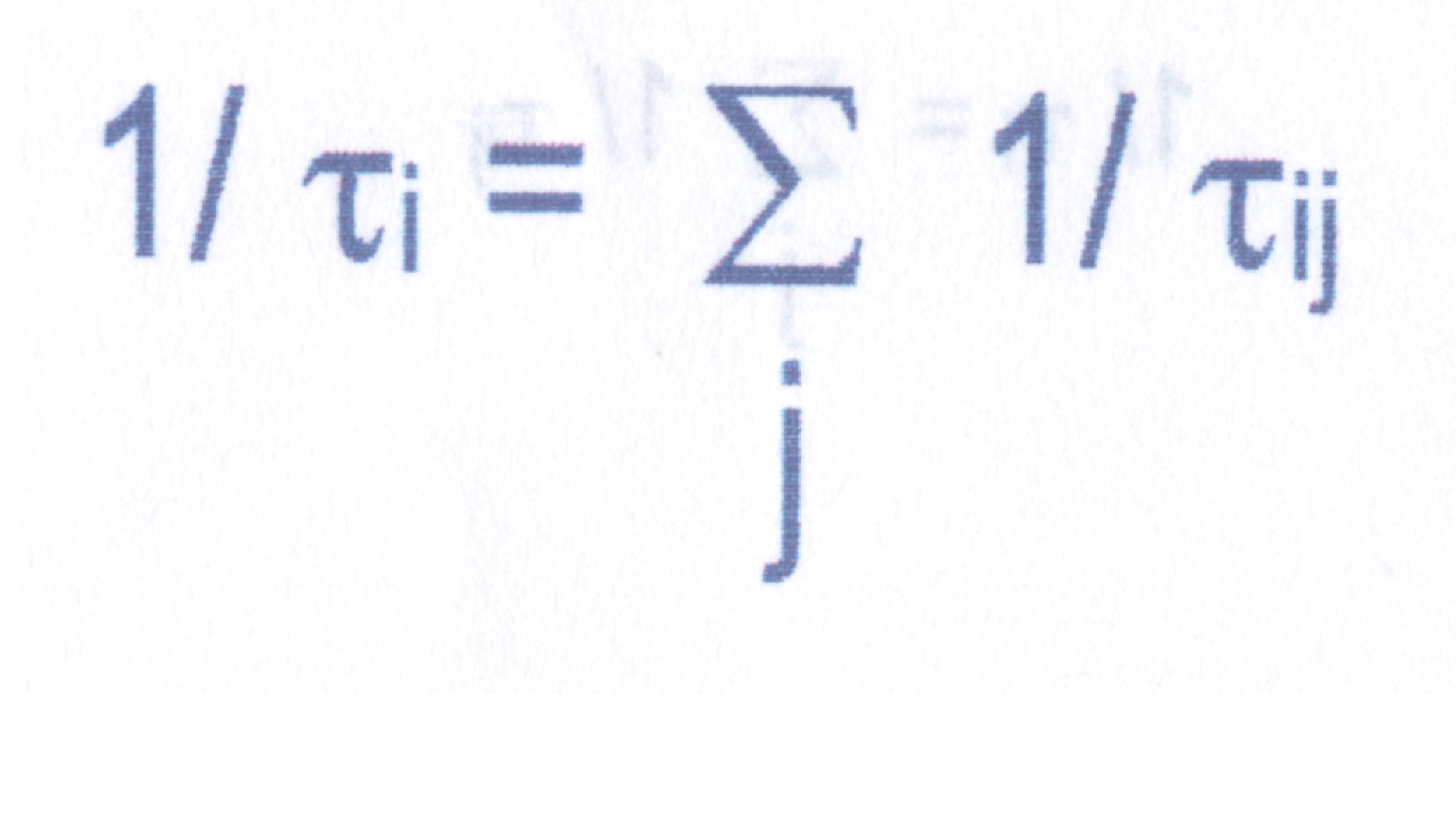
wheret _ij = 1/ P_ij , P_ij is the transition probability for the transition (radiative or non-radiative, from state ` I ’ to ` j ’ ). Lifetime of a state is the statistical measure of the time for which a population can be retained in an excited state, hence is very important parameter from laser point of view.

It is not possible to associate a single frequency n given by hn = E_j - E_i ( E_j > E_i) to the radiation emitted when an atom/ion/molecule makes radiative transition. Graphically the intensity as a function n is shown in Fig. 2.1. The full width at half maximum is called line-width and the phenomena responsible for this type of emission profile is called line-broadening. The main broadening mechanisms are:

(a) Natural Broadening: This is due to uncertainty principle which states that energy width D E of an energy level that has a minimum uncertainty in its lifetime D t is given by D ED t = h / 2 p or D E = h / 2p D T » h / 2p t where t is the lifetime of the state. This type of broadening gives rise to Lorentzian-shaped emission spectrum. In case of isolated atom/ion/molecule, this is the minimum emission line-width. However, in practical systems where the atom/ion/molecule is not isolated the lifetime of the state with population decreases due to interaction with other atoms/ions/molecules resulting in broadening of emission spectrum. This broadening is homogeneous (all atoms/molecules/ions are effected in the same way and extent ) and produces Lorentzian-shaped profile of the emitted radiation. This type of broadening is very important in case of solids and liquid lasers.

(b) Doppler Broadening : In case of gases Doppler Broadening is the dominating broadening mechanism. The Doppler broadening results from the thermal distribution of velocities of atoms/ions/molecules- some are moving directly towards the observer or away from the observer, while some are moving partially towards the observer or away from the observer. This Doppler shift results in Gaussian emission spectrum and is an inhomogeneous phenomena as the extent of Doppler shift depends on the velocity of the moving atom/ion/molecule with respect the observer.

2.2.1   Gain in Atoms / Ions/ Molecules

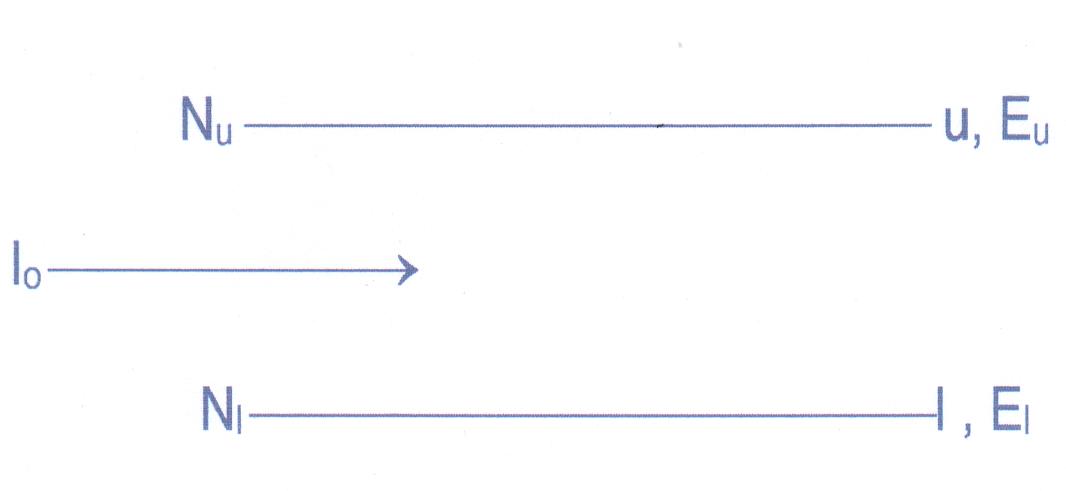
Consider a system with two energy levels ‘ u ‘ and ‘ l ‘ . N_u is population of ‘ u ‘ while N_l is that of ‘ l ‘ while E_u & E_l denote the energies. Let a beam of electromagnetic radiation of intensity I_o be incident on this system. The frequency n of the incident radiation is such that ( hn = E_u - E_l ). For simplicity, it is assumed that only radiative transition are allowed between these two levels and the levels are non-degenerate. Number of upward transition (absorption) from ‘ l ‘ to ‘ u ‘ in the frequency range D n are N_l B_ul D n r (n ), where B_ul is Einstein B coefficient and r (n ) is the density of the radiation field incident on the system . Number of downward transition due to spontaneous emission is N_u A_ul where A _ul is Einstein A co-efficient and due to stimulated emission is N_u B_{ul D n} r (n ) ( B_ul = B_lu , all these Einstein coefficients are transition probability per unit time ). So we have

N_e B_ul D n r (n ) – upward transitions

N_u A_ul + N_u B_ul D n r (n ) – downward transitions

r (n ) can be expressed in terms of the intensity of the radiation field by the standard equation

I(n ) = r (n ) . c or I(n )D n = r (n ) D n .c

or r (n ) D n = I/c . So in terms of intensity we have

N_e B_ul I/c – upward transitions

N_u A_ul + N_u B_ul (I/c) – downward transitions

The charge in the amount of energy per unit time (intensity times cross-sectional area of the beam) when the beam passes through a region ( consisting of the medium characterized by the energy level) of length dz and cross-section area dA within the medium can be expressed as the difference between the number of transitions per unit time upward and stimulated number of transitions downward, neglecting the downward transitions due to spontaneous emission which being isotropic contributes very little to the beam. So we have

[I ( z + dz) – I(z)] dA

= [N_u - N_e] B_ul I/c . h n

d I /d z = [ N_u – N_e] B_ul. h n (I/ c )= k I

where k = [ N_u – N_e ] B_ul hn /c is independent of z . This is a standard differential equation, where solution can be expressed as

I = I_o e^kz , I_o is the initial intensity of the beam when it is incident on the medium.

If k is –ve , I < I_o , we have absorption

If k is +ve , I > I_o, we have amplification.

k = [ N_u – N_e] B_ul hn /c

k is –ve if N_u< N_e – absorption which is normally the case

k is +ve if N_u > N_e – amplification.

To have gain in atoms/ions/molecules we need to have more population in the upper level. compared to the lower level which is violation of Boltzmann distribution. This is called ‘ population inversion’ and is necessary to obtain gain for the laser medium. The levels in general are degenerate and if g_u & g_l are the degeneracy of levels ‘ u ‘ and ‘ l ‘ we have

k = ( g_l N_u – g_u N_e) B_ul (hn /c) so that the condition for amplification is

g_l N_u– g_u N_e > 0

N_u > [g_u/g_l ] N_e or [ N_u g_l / N_l g_u > 1]

This is ‘ necessary condition’ for amplification.

A beam of electromagnetic radiation of initial interest I_o will be amplified if it passes through a system of atoms/ions/molecules provided these exits a population inversion between two levels ‘ u ‘ & ‘ l ‘ so that E_u – E_l = hn , where n is the frequency of photons associated with the incident radiation. The amplification is given by the equation

I = I_o e ^kz where k = [ g_l N_u – g_uN_l ] B_ul ( hn /c)

The exponential growth of I cannot be sustained for long because after some point in time the population inversion (g_lN_u – g_uN_l) cannot support the exponential growth. In other words I reaches a maximum value I_sat above which the beam no longer grows exponentially. I_sat is called ‘ saturation’ intensity and a system (atoms/ions/molecules) with population inversion should allow the saturation of intensity to occur as intensity saturation is ‘ sufficient condition’ for laser oscillation. So in a laser oscillation, a gain medium (atoms/ions/molecules/ ‘free ‘ electrons with population inversion) when placed in resonator, a radiation beam starts with spontaneous emission which is amplified during its traverse between the resonator mirrors, reaches a saturation valve when gain = loss in the resonator cavity, the losses in the resonator consist of (i) scattering in the laser medium (ii) absorption in the mirrors and other optical surfaces (iii) diffraction loses and (iv) transmission of the output–coupler which is the useful output from the laser. If population inversion (g_lN_u – g_uN_l) can be maintained continuously we have CW laser output otherwise we have pulsed output. Next we discuss the methods used to obtain population inversion.

2.2.2  Pump for a Laser Oscillation

The aim of the pump is to obtain population inversion in atoms/ions/molecules, which may be in form of a solid, liquid or gas. In solids and liquids ‘ optical pumping ‘ is employed for creating population inversion. In optical pumping selective excitation of the upper laser level is obtained by the absorption of photons provided by high pressure Xenon flash lamp or by a laser. In case of gases or vapours, electrical discharge (both pulsed as well as DC) is used as a pump. Also proper gases are added to the discharge to help in the creation of population inversion.

2.2.3  Optical Resonator

A 100% reflecting mirror and a partially reflecting mirror (output coupler) in general, constitute an optical resonator. If R₁ and R₂ are the radii of curvature of two mirrors separated by d then the condition to have a stable resonator is

0 < [(1 – d)/ R₁)][(1 –d)/ R₂] £ 1

The reflectivity of the output coupler depends upon the magnitude of the gain of the medium.

2.3   Lasers Used for Quality Control

2.3.1   He – Ne Lasers

Operating wavelengths 543.0 nm, 594.0 nm, 612.0nm, 632.8 nm, 1150 nm, 3390nm

Most popular is 632.8 nm (red He – Ne)

Power: 0.5 – 35 mw

Mode: TEM_oo

Polarization: Random or linear

Beam diameter: 0.5 – 1.5 mm at 1/e² points

Beam divergence: 1 – 2 mrad

Power drift: 5% over 8 hours

Amplitude Noise: 0.5%

Lifetime: 20,000 hours.

2.3.2   Diode Lasers

Operating wavelength : 780nm, 670nm, 660nm, 650nm, 635nm, green diode lasers have fast arrived in the market.

Output power : 5 – 500mw

Beam divergence : Diodes have inherently poor divergence. However, it can be improved a lot by using corrective optics.

2.3.3   CW Laser Pumped Dye Lasers

Operating wavelength : 370 – 900nm, Tunable using different dyes

Maximum power: 2 – 7.5 w

Beam divergence : 0.5 mrad

2.3.4   Pulsed Dye Lasers

Peek Power : 20 mw ( 150mj energy per pulse)

Average Power : 15 W

Pulse duration = 2 – 3 ns

Beam divergence = 0.5 mrad

Pulse repetition rate = 1 1000 Hz

Spectral linewidth = 1.2 GHz

He – Ne and diode lasers find applications in alignment check, dimensional control and defect detection while dye lasers are used in on-line monitoring of products in chemical industry.