We analyse the stability of a heavy inextensible cable traveling at constant velocity at an angle against the gravity. The governing equation for transverse in-plane vibrations are derived. Modal and transient solutions are obtained computationally, at different velocities of operation. The margin of stability is identified from the critical values of the velocity. Results are being double-checked with simple experiments conducted on a lab-scale set-up. Energy study confirms of a continuous energy influx into the system; indicating that it is nonconservative. Effects of external damping on the stability of such system is also analysed.

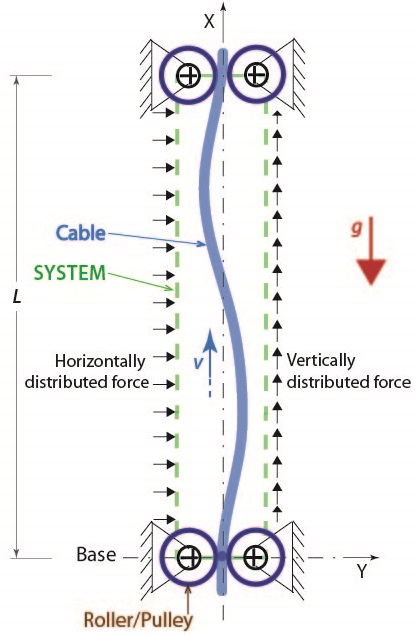Vertically traveling cables are often used to operate elevators in skyscrapers and mines (ground and under water). Understanding the dynamics of cable systems employed in these application is important to arrive at the critical speed of operation and to design control systems.

Several research groups have investigated the dynamics of horizontal string/cable, or beam, traveling between fixed rollers separated by a finite distance. In these studies the major concern was to obtain through modal analysis the relation between the system's velocity and its natural frequency.

We have studied the dynamics of a vertically traveling heavy cable through rollers fixed in the inertial frame. The cable was modeled as an inextensible string, traveling at a constant velocity. The roller supports were taken as rigid and frictionless. Equation of motion of the cable for transverse in-plane vibrations was derived and solved for the eigenfrequencies. Our preliminary analysis showed that the heavy cable in these conditions is stable in a small regime, indicated by its critical velocity.

Sloshing refers to the motion of a liquid inside a container. It may be caused by any disturbance of partially-filled liquid containers. This motion of the fluid is typically uncontrolled and hence affects the dynamics of the container in a non-trivial manner. For example, in a partially-filled container, the oscillation of the liquid shifts the system’s center of mass. To understand this motion, we need to know how the oscillation of the fluid depends upon the motion of the container, forces acting on it and the shape of the container. An exact analytical understanding of sloshing is difficult, and even computations are not certainly straightforward.

Liquid propellants constitute the largest part of the total mass of many spacecrafts. Sloshing of liquid fuel in the fuel tanks affects the attitude dynamics of the spacecraft, specifically, it’s orientation and angular velocity. The deviation of the actual attitudinal motion from the predicted rigid body motion, may allow us to know the life remaining in the spacecraft provided we are able to quantify, to some extent, the effects of fuel sloshing on the spacecraft’s motion.

We approximate the motion of the fuel in it’s first mode by the motion of a spherical pendulum whose length and mass are related to the amount of fuel remaining. The spacecraft is modeled as a rigid body. To compare with a lab-scale experiment we will, in fact, take the spacecraft to be suspended from a point on the Earth’s surface. Thus, the system is taken as a spherical compound pendulum with an internally suspended spherical simple pendulum.

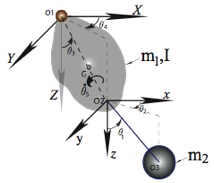We derive the equations of motion of such a system that can be integrated, provided we know the length and mass of the spherical simple pendulum. Other system parameters, such as, the mass of spacecraft, it’s orientation and inertia are assumed known. Then, from the experiment we obtain physical parameters -- Euler’s angles and their rates. We identify the length and mass of the spherical simple pendulum that best match the obtained data, which is in the form of the Euler angles and Euler rates, over the entire period of the experiment. This allows us to estimate the amount of fuel remaining. The results obtained on integration of the equations matched fairly with the experimental data.