| |
|
Syllabus:
|
Pre-requisite: None
Single Variable Calculus: Real number system: Completeness axiom, density of rationals (irrationals) in 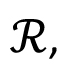 , convergence of a sequence, Sandwich theorem, Monotone sequences, Cauchy Criterion, Subsequence, Every bounded sequence has a convergent subsequence, convergence of a sequence satisfying Cauchy criterion, Limits and Continuity of functions, Boundedness of a continuous function on [a, b], Existence of max of a continuous function on [a, b], Intermediate value property, Differentiability, Necessary condition for local maxima, Rolles theorem and Mean Value theorem, Cauchy mean value theorem, L `Hospital rule, Fixed point iteration method (Picard's method), Newton's method, Increasing and decreasing function, Convexity, Second derivative test for max and min, Point of Inflection, Curve Sketching, Taylor's theorem and remainder, Convergence of series, Geometric and Harmonic Series, Absolute convergence, Comparison test, Cauchy Condensation test: , convergence of a sequence, Sandwich theorem, Monotone sequences, Cauchy Criterion, Subsequence, Every bounded sequence has a convergent subsequence, convergence of a sequence satisfying Cauchy criterion, Limits and Continuity of functions, Boundedness of a continuous function on [a, b], Existence of max of a continuous function on [a, b], Intermediate value property, Differentiability, Necessary condition for local maxima, Rolles theorem and Mean Value theorem, Cauchy mean value theorem, L `Hospital rule, Fixed point iteration method (Picard's method), Newton's method, Increasing and decreasing function, Convexity, Second derivative test for max and min, Point of Inflection, Curve Sketching, Taylor's theorem and remainder, Convergence of series, Geometric and Harmonic Series, Absolute convergence, Comparison test, Cauchy Condensation test: 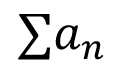 converges converges 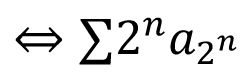 converges for converges for 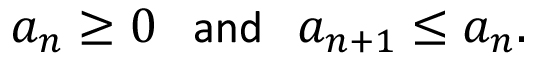 Example Example 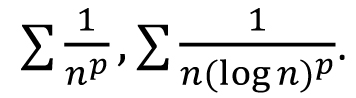 . Ratio test, Root test, Examples, Leibniz' theorem, Power series, Radius of convergence, Taylor Series, Maclaurin Series, Introduction to Riemann Integration, Integrability, The Integral existence theorem for continuous functions and monotone functions, Elementary properties of integral, Fundamental theorems of Calculus, Trapezoidal approximation, Simpson's Rule, Improper integral of first and second kind, Comparison test, Absolute convergence, Application of definite integral, Area between two curves, Polar coordinates, Graphs of polar coordinates, Area between two curves when their equations are given in polar coordinates, Volumes by slicing, Volumes by Shells and Washers, Length of a curve, Area of surface of revolution, Pappus's theorem, Review of vector algebra, Equations of lines and planes, Continuity and Differentiability of vector functions, Arc length for space curves, Unit tangent vector, Unit normal and curvature to plane and space curves, Binormal, Functions of several variables, Continuity, Partial derivatives, Differentiability, Differentiability implies continuity, Increment theorem, Chain rule, Gradient, Directional derivatives, Tangent plane and Normal line, Mixed derivative theorem, Mean value theorem, Minima and Saddle point, Necessary and sufficient conditions for Maxima, minima and Saddle point, The method of Lagrange multipliers, Double Integral, Fubini's theorem, Volumes and Areas, Change of variable in double integral. Special cases: Polar coordinates, Triple integral, Applications, Change of variable in triple integral. Special cases: Cylindrical and Spherical coordinates, Surface area, Surface integral, Line integrals, Green's theorem, Vector fields Divergence and Curl of a vector field, Stoke's theorem, The divergence theorem. . Ratio test, Root test, Examples, Leibniz' theorem, Power series, Radius of convergence, Taylor Series, Maclaurin Series, Introduction to Riemann Integration, Integrability, The Integral existence theorem for continuous functions and monotone functions, Elementary properties of integral, Fundamental theorems of Calculus, Trapezoidal approximation, Simpson's Rule, Improper integral of first and second kind, Comparison test, Absolute convergence, Application of definite integral, Area between two curves, Polar coordinates, Graphs of polar coordinates, Area between two curves when their equations are given in polar coordinates, Volumes by slicing, Volumes by Shells and Washers, Length of a curve, Area of surface of revolution, Pappus's theorem, Review of vector algebra, Equations of lines and planes, Continuity and Differentiability of vector functions, Arc length for space curves, Unit tangent vector, Unit normal and curvature to plane and space curves, Binormal, Functions of several variables, Continuity, Partial derivatives, Differentiability, Differentiability implies continuity, Increment theorem, Chain rule, Gradient, Directional derivatives, Tangent plane and Normal line, Mixed derivative theorem, Mean value theorem, Minima and Saddle point, Necessary and sufficient conditions for Maxima, minima and Saddle point, The method of Lagrange multipliers, Double Integral, Fubini's theorem, Volumes and Areas, Change of variable in double integral. Special cases: Polar coordinates, Triple integral, Applications, Change of variable in triple integral. Special cases: Cylindrical and Spherical coordinates, Surface area, Surface integral, Line integrals, Green's theorem, Vector fields Divergence and Curl of a vector field, Stoke's theorem, The divergence theorem.
Reference materials:
-
Thomas and Finney: "Calculus and Analytical Geometry", 9th Edition, Addison and Wesley Publishing Company.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 101
Linear Algebra: Matrices, System of linear equations, Gauss elimination method, Elementary matrices, Invertible matrices, Gauss-Jordon method for finding inverse of a matrix, Determinants, Basic properties of determinants. Cofactor expansion, Determinant method for finding inverse of a matrix, Cramer's Rule, Vector space, Subspace, Examples, Linear span, Linear independence and dependence, Basis, Dimension, Extension of a basis of a subspace, Intersection and sum of two subspace, Examples. Linear transformation, Kernel and Range of a linear map, Rank-Nullity Theorem. Rank of a matrix, Row and column spaces, Solvability of system of linear equations, some applications Inner product on 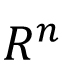 Cauchy-Schwartz inequality, Orthogonal basis, Gram-Schmidt orthogonalization process. Orthogonal projection, Orthogonal complement, Projection theorem, Fundamental subspaces and their relations, Applications (Least square solutions and least square fittings). Eigen-values, Eigen-Vectors, Characterization of a diagonalizable matrix. Diagonalization: Example, An application. Diagonalization of a real symmetric matrix. Representation of real linear maps by matrices (optional) Cauchy-Schwartz inequality, Orthogonal basis, Gram-Schmidt orthogonalization process. Orthogonal projection, Orthogonal complement, Projection theorem, Fundamental subspaces and their relations, Applications (Least square solutions and least square fittings). Eigen-values, Eigen-Vectors, Characterization of a diagonalizable matrix. Diagonalization: Example, An application. Diagonalization of a real symmetric matrix. Representation of real linear maps by matrices (optional)
Ordinary differential equations: Introduction to DE, Order of DE, First Order ODE F(x,y,y')=0. Concept of solution (general solution, singular solution, implicit solution etc.), Geometrical interpretations (direction fields, isoclines), Separable form, Reduction to separable form, Exact equations, Integrating factors (of the form F(x) and F(y)). Linear equations, Bernoulli equation, orthogonal trajectories. Picard's existence and uniqueness theorem (without proof), Picard's iteration method. Numerical methods: Euler's method, improved Euler's method. Second order linear ODE: fundamental system and general solutions of homogeneous equations, Wronskian, reduction of order. Characteristic equations: real distinct roots, complex roots, repeated roots. Non-homogeneous equations: undetermined coefficients. Non-homogeneous equations: variation of parameters. Extension to higher order differential equations, Euler-Cauchy equation. Power series solutions: ordinary points (Legendre equation). Power series solutions: regular singular points (Bessel equation), Frobenius method, indicial equations. Legendre polynomials and properties, Bessel functions and properties, Sturm comparison theorem, Sturm-Liouville boundary value problems, orthogonal functions. Laplace transform: Laplace and inverse Laplace transforms, first shifting theorem, existence, transforms of derivative and integral. Laplace transform: Differentiation and integration of transforms, unit step function, Second shifting theorem. Laplace transform: Convolution and applications, initial value problems.
Reference materials:
-
G. Strang: Linear Algebra, Introduction to linear algebra, 41 Edition, Wellesley Cambridge Press.
-
G. F. Simmons: Ordinary Differential Equations, Differential equations with applications and historical notes, 2nd Edition.
|
|
Credits:
|
11
|
|
Duration:
|
Modular (To be offered in the first half)
|
|
Credits:
|
3-1-0-0 (6)
|
|
Prerequisites:
|
N/A
|
|
Syllabus:
|
Real number system: Completeness axiom, density of rationals (irrationals) in $\mathbb{R}$, convergence of a sequence, Sandwich theorem, Monotone sequences, Cauchy Criterion, Subsequence, Every bounded sequence has a convergent subsequence, convergence of a sequence satisfying Cauchy criterion, Limits and Continuity of functions, Boundedness of a continuous function on $[a, b]$, Existence of max of a continuous function on $[a,b]$, Intermediate value property, Differentiability, Necessary condition for local maxima, Rolles theorem and Mean Value theorem, Cauchy mean value theorem, L `Hospital rule, Fixed point iteration method (Picard's method), Newton's method, Increasing and decreasing function, Convexity, Second derivative test for max and min, Point of Inflection, Curve Sketching, Taylor's theorem and remainder, Convergence of series, Geometric and Harmonic Series, Absolute convergence, Comparison test, Cauchy Condensation test. Ratio test, Root test, Examples, Leibniz' theorem, Power series, Radius of convergence, Taylor Series, Maclaurin Series, Introduction to Riemann Integration, Integrability, The Integral existence theorem for continuous functions and monotone functions, Elementary properties of integral, Fundamental theorems of Calculus, Trapezoidal approximation, Simpson's Rule, Improper integral of first and second kind, Comparison test, Absolute convergence.
|
|
Duration:
|
Modular (To be offered in the second half)
|
|
Credits:
|
3-1-0-0 (6)
|
|
Prerequisites:
|
MTH111A
|
|
Syllabus:
|
Application of definite integral, Area between two curves, Polar coordinates, Graphs of polar coordinates, Area between two curves when their equations are given in polar coordinates, Volumes by slicing, Volumes by Shells and Washers, Length of a curve, Area of surface of revolution, Pappus's theorem, Review of vector algebra, Equations of lines and planes, Continuity and Differentiability of vector functions, Arc length for space curves, Unit tangent vector, Unit normal and curvature to plane and space curves, Binormal, Functions of several variables, Continuity, Partial derivatives, Differentiability, Differentiability implies continuity, Increment theorem, Chain rule, Gradient, Directional derivatives, Tangent plane and Normal line, Mixed derivative theorem, Mean value theorem, Minima and Saddle point, Necessary and sufficient conditions for Maxima, minima and Saddle point, The method of Lagrange multipliers, Double Integral, Fubini's theorem, Volumes and Areas, Change of variable in double integral. Special cases: Polar coordinates, Triple integral, Applications, Change of variable in triple integral. Special cases: Cylindrical and Spherical coordinates, Surface area, Surface integral, Line integrals, Green's theorem, Vector fields Divergence and Curl of a vector field, Stoke's theorem, The divergence theorem.
|
|
Duration:
|
Modular (To be offered in the first half)
|
|
Credits:
|
3-1-0-0 (6)
|
|
Prerequisites:
|
MTH 111A
|
|
Syllabus:
|
-
System of linear equations and matrices: Matrices, System of linear equations; Elementary matrices, Invertible matrices, Gauss-Jordon method for finding inverse of a matrix; Determinants, Basic properties of determinants, Cofactor expansion, Determinant method for finding inverse of a matrix, Cramer’s Rule. (5 lectures)
-
Vector space: Vector space, Subspace, Examples; Linear span, Linear independence and dependence, Examples; Basis, Dimension, Extension of a basis of a subspace, Intersection and sum of two subspaces, Examples. (4 lectures)
-
Linear transformation: Linear transformation, Kernel and range of a linear map, Ranknullity theorem; Rank of a matrix, Row and column spaces, Solvability of system of linear equations. (3 lectures)
-
Inner product space: Inner product, Cauchy-Schwartz inequality, Orthogonal basis, Gram-Schmidt orthogonalization process; Orthogonal projection, Orthogonal complement, Projection theorem; Fundamental subspaces and their relations, Application (Least square solutions and least square fittings). (3 lectures)
-
Eigenvalue and eigenvector: Eigenvalues, Eigenvectors; Characterization of a diagonalizable matrix, Example, Diagonalization of a real symmetric matrix; Representation of a real linear maps by matrices (optional). (4 lectures)
|
|
Duration:
|
Modular (To be offered in the first half)
|
|
Credits:
|
3-1-0-0 (6)
|
|
Prerequisites:
|
MTH111A, MTH112A, MTH113A
|
|
Syllabus:
|
-
First order ODEs: Introduction to differential equations, Concept of solution, Geometrical interpretations; Separable form, Reduction to separable form; Exact equations, Integrating factors ; Linear equations, Bernoulli equations, orthogonal trajectories; Picard’s existence and uniqueness theorem (without proof), Picard’s iteration method; Numerical methods: Euler’s method. (6 lectures)
-
Second order linear ODEs: Improved Euler’s method. Fundamental system and general solutions of homogeneous equations, Wronskian, Reduction of order; Characteristic equations: real distinct roots, complex roots, repeated roots; Nonhomogeneous equations: methods of undetermined coefficients and variation of parameters; Extension to higher order differential equations, Euler-Cauchy equation, Qualitative properties of solutions, Sturm comparison theorem. (6 lectures)
-
Series solutions of ODEs: Ordinary points, Power series solutions; Regular singular points, Frobenius method; Legendre polynomials; Bessel functions. (3 lectures)
-
Boundary value problems: Sturm-Liouville boundary value problems, Orthogonal functions. (1 lecture)
-
Laplace transform: Laplace and inverse Laplace transforms, First shifting theorem, Transforms of derivative and integral, Differentiation and integration of transforms; Unit step function, Second shifting theorem, Convolution, Solution of initial value problems. (3 lectures)
|
|
Syllabus:
|
Pre-requisite: MTH 101, None for M.Sc. 2 yr
Probability:- Axiomatic definition, properties, conditional probability, Bayes' rule and independence of events. Random variables, distribution function, probability mass and density functions, expectation, moments, moment generating function, Chebyshev's inequality. Special distributions; Bernoulli, binomial, geometric, negative binomial, hypergeometric, Poisson, exponential, gamma, Weibull, beta, Cauchy, double exponential, normal. Reliability and hazard rate, reliability of series and parallel systems. Joint distributions, marginal and conditional distributions, moments, independence of random variables, covariance and correlation. Functions of random variables. Weak Law of large numbers and Central limit theorems.
Statistics:- Descriptive statistics, graphical representation of the data, measures of location and variability. Population, sample, parameters. Point estimation; method of moments, maximum likelihood estimator, unbiasedness, consistency. Confidence intervals for mean, difference of means, proportions. Testing of hypothesis; Null and Alternate hypothesis, Neyman Pearson fundamental lemma, Tests for one sample and two sample problems for normal populations, tests for proportions.
Reference materials:
-
Robert V. Hogg, J.W. McKean, and Allen T. Craig: Introduction to Mathematical Statistics, Seventh Edition, Pearson Education, Asia.
-
Edward J Dudewicz and Satya N. Mishra: Modern Mathematical Statistics, Wiley.
|
|
Credits:
|
11 |
|
Syllabus:
|
Pre-requisite: MTH 101
Complex Numbers, Polar form, De-Moivre's formula, convergent sequence, continuity, Complex differentiation, Cauchy-Riemann equation, Applications, Analytic functions and Power series, Derivative of a power series, Exponential function, Logarithmic function and trigonometric functions, Contour and Contour integral, Anti-derivative, ML inequality, Cauchy's theorem, Cauchy Integral formula, examples, Evolution of contour integrals, Derivatives of analytic functions, Cauchy's estimate, Liouville theorem, Fundamental theorem of Algebra, Morera's theorem (without proof), Taylor's theorem, Examples, Computation of Taylor's series. Zeros of Analytic functions. Identity theorem, Uniqueness theorem, Applications, Maximum modulus principle, Laurent series, Computation of Laurent expansion, Cauchy residue theorem, Poles, Residue at a pole, Examples, Evaluation of real improper integrals of different forms, Linear fractional transformations.
Reference materials:
-
E. Kreyszig, Advanced Engineering Mathematics.
-
R. V. Churchill and J. W. Brown, Complex Variables and Applications.
|
|
Credits:
|
6
|
|
Syllabus:
|
Pre-requisite: MTH 102
Introduction to PDE, Linear, non-linear (semi-linear quasilinear) examples, Order of a PDE, Strum-Liouville boundary values problems: Introduction, examples, orthogonal functions, Strum-Liouville expansion, Fourier series and its convergence, Fourier series of arbitrary period, Sine and Cosine series. Half-range expansion, Fourier integrals, Fourier-Legendre series, Fourier-Bessel series, First order (linear and semi-linear) PDEs, interpretation, method of characteristics, general solutions, First order quasi-linear PDEs, interpretation, method of characteristics, general solutions, Classification of 2nd order PDEs, Canonical form, hyperbolic equations, parabolic equations and elliptic equations, Wave equations, D'Alemberts formula, Duhamel's principle, Solutions for initial boundary value problem. Heat equations, Uniqueness and maximum principle, applications, Solutions for initial boundary value problem. Laplace and Poisson equations, uniqueness and maximum principle for Dirichlet problem, Boundary value problems in 2D (rectangular, polar), Boundary value problems in 3D (rectangular, cylindrical, spherical).
Reference materials:
-
E. Kreyszig, Advanced Engineering Mathematics.
|
|
Credits:
|
6
|
|
Credits:
|
3-1-0-0 (11)
|
|
Prerequisites:
|
None
|
|
Objectives:
|
This is a theoretically rooted introductory course on fundamental concepts in probability. The objective is to lay a foundation for future courses in probability, statistics, and data science.
|
|
Course Contents:
|
1. Basic definitions and ideas such as random experiment, sample space and event, Classical definition and relative frequency definition of probability, Axiomatic definition of probability, Elementary properties of probability function, Probability inequalities such as Boole’s inequality and Bonferroni inequality. [5 lectures]
2. Conditional probability and its basic properties, Examples of conditional probability and multiplication law, Theorem of total probability and related examples, Bayes theorem and related examples, Independent events. [5 lectures]
3. Random variables and their distribution function, Induced probability space, Discrete and continuous random variables, Function of random variables (Discrete and Continuous), Expectation and moments of random variables, MGF of random variables and its application, Markov, Chebyshev and Jensen’s inequality, Characteristics function and its application. [7 lectures]
4. Standard discrete distributions and their properties (e.g., Bernoulli, Binomial, Geometric, Negative Binomial, Hypergeometric, Poisson) Standard continuous distributions and their properties (e.g., Normal, Exponential, Gamma, Beta, Cauchy). [5 lectures]
5. Random vectors and their joint distribution functions, Marginal distribution, independent random variables, Conditional distribution of random vectors/variables, Expectation and moments of random vectors, Conditional Expectation, variance and covariance and their applications. [7 lectures]
6. Idea of limiting distribution, Convergence in distribution and probability, and related results, Convergence of moments and almost sure convergence, Various examples and counter examples. [6 lectures]
7. Weak law of large numbers, Central limit theorem, Applications, e.g., continuous mapping theorem and delta method. [5 lectures]
|
|
References:
|
1. Hogg, R. V., McKean, J., Craig, A. T. (2005). Introduction to Mathematical Statistics. Pearson Education.
2. Hoel, P. G., Port, S. C., Stone, C. J. Introduction to Probability Theory, 1971. Houghton Mifflin, Boston, MA.
3. Boes, D. C., Graybill, F. A., Mood, A. M. (1982). Introduction to the Theory of Statistics. McGraw-Hill International Book Company.
4. Ross, S. M. (2014). Introduction to Probability Models. Academic press.
|
Departmental Courses
|
Credits:
|
L-T-P-D[C]: 3-0-0-0 [9]
|
|
Prerequisites:
|
At least one of MTH 302/CS 340/MTH 401 and/or consent of the Instructor.
|
|
Objectives:
|
The goal of this course is to serve as an introduction to Computability Theory. The intended audience are advanced undergraduate and beginning graduate students who have had exposure to some proof based course in the theory of computation.
|
|
Syllabus:
|
Review of models of computation and Church-Turing thesis, Universal partial computable function and Kleene’s S-n-m theorem, C.e. sets, Examples of algorithmic undecidability: MRDP theorem, Boone-Novikov theorem, Wang tiling problem, Strong reductions and Myhill’s theorem, Simple and immune sets, Hyperimmune sets, Oracle computation, Turing degrees and the jump operator, Arithmetical hierarchy, Low and high sets, Martin’s high domination theorem, Forcing constructions: Kleene-Post, Spector’s exact pair, Recursively pointed trees and minimal degrees, Priority constructions: Friedberg-Mucnik theorem, Sacks splitting theorem, Computable ordinals and the hyperarithmetical hierarchy, Solovay’s theorem, Measure and category on the Cantor space, Algorithmic genericity and randomness, Schnorr/Martin-Lof randomness and van-Lambalgnen theorem, Kolmogorov complexity and randomness, Current research topics.
|
|
References:
|
1. Robert Soare, Turing Computability: Theory and Applications, Springer 2016.
2. Andre Nies, Computability and Randomness, Oxford University Press 2009.
3. Robert Downey and Denis Hirschfeldt, Algorithmic randomness and Complexity, Springer 2010.
|
|
Syllabus:
|
Pre-requisite: MTH102, None for M.Sc. 2yr
Matrices: Elementary matrices, invertible matrices, Gauss-Jordon method, determinant, Systems of linear equations and Cramer's Rule. Vector spaces: Fields, Vector spaces over a field, subspaces, Linear independence and dependence, existence of basis, coordinates, dimension. Linear Transformations: Rank Nullity Theorem, isomorphism, matrix representation of linear transformation, change of basis, similar matrices, linear functional and dual space. Inner product spaces: Cauchy-Schwarz's inequality, Gram-Schmidt orthonormalization, orthonormal basis, orthogonal projection, projection theorem, four fundamental subspaces and their relations (relation between null space and row space; relation between null space of the transpose and the column space). Diagonalization: Eigenvalues and eigenvectors, diagonalizability, Invariant subspaces , adjoint of an operator, normal, unitary and self adjoint operators, Schur's Lemma, diagonalization of normal matrices, spectral decompositions and spectral theorem, applications of spectral theorem, Cayley-Hamilton theorem, primary decomposition theorem, Jordon canonical form, minimal polynomials, Introduction to bilinear and Quadratic forms: Bilinear and quadratic forms, Sylvester's law of inertia. Some applications: Lagrange interpolation, LU,QR and SVD decompositions, least square solutions, least square fittings, pseudo inverses.
Reference materials:
-
Kenneth Hoffman and Ray Kunze: Linear Algebra, PHI publication.
-
Gilbert Strang: Linear Algebra and Its Applications, 4th edition.
-
Sheldon Axler: Linear Algebra Done Right, UTM, Springer.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 102, None for M.Sc. 2yr
Basic set theory: Unions, Intersections, Pairs, Powers, Relations and Functions, Partial Orders, Numbers, Peano's Axioms, Mathematical Induction, Finite and Infinite Sets, Families of sets: Product of sets(finite and infinite), More on relations and functions, Schroder-Bernstein Theorem, Countable and Uncountable Sets, Axiom of Choice, Zorn's Lemma, Cardinals and ordinals, Integers, Divisibility in Integers, GCD, Bezout's identity, modular arithmetic, Chinese remainder theorem, Fermat's little theorem, Euler Phi-function, Permutation, Combinations, Circular permutations, Binomial and Multinomial theorems, Solutions in nonnegative integers, Balls into Boxes-Pigeon-hole Principle, Inclusion-Exclusion Principle, Recurrence Relations, Generating Functions, generating functions from recurrence relation.
Reference materials:
-
Kenneth Rosen: Discrete Mathematics and Its Applications, McGraw Hill Education; 7th edition.
-
Donald Knuth, Oren Patashnik, and Ronald Graham: Concrete Mathematics, Addison-Wesley Professional.
-
David M. Burton: Elementary Number Theory.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH102, None for M.Sc. 2yr
Group theory: Binary operation, and its properties, Definition of a group, Groups as symmetries, Examples: cyclic, dihedral, symmetric, matrix groups, Subgroups, Cosets, normal subgroups and quotient groups, Conjugacy classes, Lagrange's theorem, The isomorphism theorems, Direct and semi-direct products, Group automorphisms, Symmetric group and alternating group, Actions of groups on sets, Cayley's theorem, orbit and stabilizers, Class equations, p-groups, Sylow's theorem and applications: simplicity of groups, Classification of finite abelian groups. (Time permitting: Finitely-generated abelian groups, Free groups, Composition series, Jordan-Hölder theorem, Nilpotent and solvable groups). Ring Theory: Definition and examples, Ring homomorphism, Ideals and Quotient rings, Chinese Remainder Theorem, Integral Domain and quotient fields, Unique factorization domain, Principal Ideal domain, Euclidean domain, Gauss lemma, Polynomial Rings, Irreducibility of Polynomials, Ring of Gaussian Integers.
Reference materials:
-
J. Gallian: Contemporary Abstract Algebra, Narosa books Pvt. Ltd.
-
I. N. Herstein: Topics in Algebra, Wiley.
-
D. S. Dummit and R.M. Foote, Abstract Algebra, Wiley.
-
M. Artin, Algebra, PHI.
-
N. Jacobson, Basic Algebra I, Basic Algebra II, Dover Publications.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH101, MTH 102, None for M.Sc. 2yr
Fourier series, Convolutions, Good kernels, Cesaro and Abel Summable, Convergence of Fourier series: Mean square, Pointwise convergence, Applications: Weyl equi-distribution, Isoperimetric inequality, Construction of continuous but nowhere differentiable function, Finite Fourier Analysis: on abelian groups, Characters as a total family, Fourier inversion and Plancherel formula, Dirichlet's Theorem: A little elementary number theory, Dirichlet's theorem, Proof of the theorem.
Reference materials:
-
E. M. Stein and R. Shakarchi: Fourier analysis: An Introduction.
|
|
Credits:
|
11 |
|
Credits:
|
3-1-0-0 (06)
|
|
Prerequisites:
|
None
|
|
Objectives:
|
This is an introductory course on linear algebra, designed to cover the prerequisite topics for Linear Estimation, Regression, Multivariate Statistics. The aim is to build a strong foundation of vector spaces and cover aspects of matrix theory in adequate details
|
|
Course Contents:
|
1. Review of finite dimensional Vector Spaces Vector spaces - Subspace - Linear independence - Basis and dimension Sum, direct sum and complement of subspaces Orthogonality and orthogonal basis - orthogonal complement [6 Lectures]
2. Matrix Algebra Preliminaries Different types of matrices - Operations of matrices - Properties of operations. [2 lectures]
3. Rank of a Matrix Row space and column space Rank - Results related to ranks of matrices. [2 lectures]
4. Determinant and Inverse of a non-singular matrix Inverse of a matrix - Properties of inverse Elementary matrix operations - Different matrix forms Determinant - Properties of determinant. [4 lectures]
5. Solution of Linear Equations Homogeneous systems - General linear systems Sweep out method for solving linear systems. [2 lectures]
6. Eigenvalues and vectors, Spectral and Singular value decomposition Characteristic roots - Eigenvectors and eigenspaces Spectral decomposition of a semi-simple matrix Singular value decomposition [3 lectures]
7. Real quadratic forms, Reduction of pair of real symmetric matrices, Extrema of quadratic forms Classification of quadratic forms - Rank and signature Definiteness of matrices - Extrema of quadratic forms [3 Lectures]
|
|
References:
|
1. Harville, D. A. (2008). Matrix Algebra from a Statistician’s Perspective. United States: Springer.
2. Ramachandra Rao, A., Bhimasankaram, P. (2000). Linear Algebra. Germany: Hindustan Book Agency.
3. Strang, G. (2006). Linear Algebra and Its Applications. India: Thomson, Brooks/Cole.
4. Lay, D. C. (2014). Linear Algebra and Its Applications. United Kingdom: Pearson Education Limited.
5. Bapat, R. (2012). Linear Algebra and Linear Models. Germany: Springer
|
|
Credits:
|
3-1-0-0 (06)
|
|
Prerequisites:
|
None
|
|
Objectives:
|
This course is an introduction to linear models and linear estimation covering concepts of estimability, optimality of linear models, best linear unbiased estimation, and estimation on linear constrained parameter spaces. Pre-requisites from linear algebra like projection matrix, generalized inverse, vector-matrix differentiation will also be covered in adequate details.
|
|
Course Contents:
|
1. Recap of important topics/results from Module I [1 Lecture]
2. Generalised Inverses, Moore-Penrose Inverse
i. Left and right inverses of a matrix - G-inverse
ii. Minimum Norm and Least Squares g-Inverse
iii. Moore-Penrose inverse. [3 Lectures]
3. Projection and Orthogonal Projection Matrices
i. Projection and projection matrices - orthogonal projectionii. Properties of projection and orthogonal projection matrices. [3 lectures]
4. Vector and Matrix Differentiation
i. Basic idea of matrix differentiation, differentiation of linear and quadraticforms, determinants
ii. Inverse of a matrix - maxima, minima of functions of several variables. [3 lectures]
5. Linear Model and Least Squares Theory of Estimation
i. Introduction to linear model and basic assumptions
ii. The Least Squares theory of estimation - Properties of Least SquaresEstimators. [4 lectures]
6. Estimability of a Linear Parametric Form
i. Non full column rank design matrixii. Unbiasedly estimable Linear Parametric functions. [2 lectures]
7. Gauss-Markov Theorem and Best Linear Unbiased Estimator
i. Class of Linear Unbiased Estimators and the Best Linear Unbiased Estimator
ii. The Gauss-Markov Theorem. [2 lectures]
8. Fisher-Cochran Theorem (matrix theoretic version) through some properties of the idempotent matrix. [1 Lecture]
9. Estimation under restriction
i. Least Squares estimation under a set of restrictions on linear parametricfunctions. [2 Lectures]
|
|
References:
|
- Harville, D. A. (2008). Matrix Algebra from a Statistician’s Perspective.United States: Springer.
- Ramachandra Rao, A., Bhimasankaram, P. (2000). Linear Algebra. Germany: Hindustan Book Agency.
- Strang, G. (2006). Linear Algebra and Its Applications. India: Thomson,Brooks/Cole.
- Lay, D. C. (2014). Linear Algebra and Its Applications. United Kingdom: Pearson Education Limited.
- Bapat, R. (2012). Linear Algebra and Linear Models. Germany: Springer.
- Christensen, R. (2013). Plane Answers to Complex Questions: The Theory of Linear Models. United States: Springer New York.
- Kshirsagar, A. M. (1983). A Course in Linear Models. Switzerland: M.Dekker.
- Sengupta, D., Jammalamadaka, S. R. (2003). Linear Models: An Integrated Approach. Singapore: World Scientific.
|
|
Credits:
|
0-0-3-2 (5)
|
|
Prerequisites:
|
None
|
|
Objectives:
|
To equip students with a fundamental computational learning base for modern data analysis. Focus will be on collecting, cleaning, and organizing data, and presenting clean insights via interactive web-based apps. Components on collaborative coding will be discussed via Google colab, cloud computing, and git. Programming languages used will be Python and R.
|
|
Syllabus:
|
The courses focuses on fundamental computational learning base for modern data analysis. Introduction to Programming for Data Science – Python, R, Rstudio, text editors, Google colab, RMarkdown, and RShiny. Introduction to git. Web scraping. Data cleaning and wrangling for numeric and non-numeric data. Standard statistical visualizations. Data and code reproducibility. Interfacing R, C++, and Python. Ethics and bias in data collection, including statistical paradoxes, data ethics, social biases in data, statistics in the media.
|
|
References:
|
- Wickham, Hadley. “Elegant graphics for data analysis.” O’Reilly Media 35.211 (2009)
- Wickham, Hadley. “Mastering shiny”. O’Reilly Media, Inc., 2021.
- Bruce, Peter, Andrew Bruce, and Peter Gedeck. “Practical statistics fordata scientists: 50+ essential concepts using R and Python”. O’Reilly Media, 2020.
- VanderPlas, Jake. “Python data science handbook: Essential tools forworking with data.” O’Reilly Media, Inc., 2016.
- Boehmke, Bradley C. “Data wrangling with R”. Springer InternationalPublishing, 2016.
- Pineau, Joelle, et al. “Improving reproducibility in machine learning research (a report from the neurips 2019 reproducibility program).” Journal of Machine Learning Research 22 (2021).
|
|
Credits:
|
1-0-2-0 (5)
|
|
Prerequisites:
|
MTH208A: Data Science Lab 1
|
|
Objectives:
|
To demonstrate concepts being learn’t in concurrent elementary statistics and probability courses. Additionally, to equip students with some modern tools of visualizations. They will also learn to write reproducible codes, and summarize their ideas with a project report. Focus will be on using software to ask questions which will be answered later in some of the more advanced courses.
|
|
Syllabus:
|
Computational implementations of linear algebra (Gauss elimination method, determinants, eigenvalues, eigenvectors, matrix decompositions, generalized inverses, computational complexity of matrix operations). Practical parallel computing, computational tools for optimization and implementation of least squares. Computational implementations of drawing samples, density functions, mass functions, summary functions, numerical integration for expectations. Copula functions, contour plots in two and higher dimensions. Dimensionality reduction for data visualization using ideas like PCA, LDA, TSNE and UMAP. Demonstrate probability inequalities, and the weak law of large numbers. Simulations for the central limit theorem.
|
|
References:
|
Recommended Books: There is no one textbook for this course, but the following would be useful references:
- Akalin, A. (2020). Computational Genomics with R. CRC Press.
- 2. Athreya, S., Sarkar, D., and Tanner, S. Probability and Statistics with Examples Using R. Online Access: https://www.isibang.ac.in/~athreya/ psweur/.
- Baclawski, K. (2008). Introduction to Probability with R. CRC Press.
- Dryden, I. L. and Marron, J. S. (2021). Object Oriented Data Analysis. CRC Press.
- Pearson, R. K. (2018). Exploratory Data Analysis Using R. CRC Press.
- Peng, R. (2012). Exploratory Data Analysis with R. Lean Publishing.
- Vinod, H. D. (2011). Hands-on Matrix Algebra Using R: Active and Motivated Learning with Applications. World Scientific Publishing Company.
- Yoshida, R. (2021). Linear Algebra and Its Applications with R. CRC
Press.
|
|
Credits:
|
3-0-1-0 (10)
|
|
Prerequisites:
|
MSO205A, MTH207A, MTH208A, or instructor’s consent.
|
|
Objectives:
|
The course introduces new and fundamental computational tools in Statistics. Focus is on the simulation and optimization techniques most often used in statistics. The course will balance both the theory and the practical implementation of the computational topics.
|
|
Syllabus:
|
Pseudorandom number generation, generating random variables (discrete and continuous) – inverse transform, accept-reject, Box-Muller transformation, ratioof-uniforms. Importance sampling (simple and weighted). Review of optimization, duality and KKT conditions. Newton-Raphson, gradient ascent, coordinate ascent. Least squares and optimization – linear regression, ridge, lasso, bridge. Logistic regression, least angle regression. Crossvalidation and bootstrap. MM and EM algorithm, mixture of Gaussians. Non-convex optimization, stochastic gradient ascent, simulated annealing. Bayesian models and Metropolis-Hastings.
|
|
References:
|
- Ross, S. M. (2012). Simulation (5th ed.). Academic Press
- Robert, C. P., Casella, G., Casella, G. (2004). Monte Carlo StatisticalMethods. New York: Springer.
- Boyd, S., Boyd, S. P., Vandenberghe, L. (2004). Convex optimization.Cambridge university press.
- James, G., Witten, D., Hastie, T., Tibshirani, R. (2013). An Introductionto Statistical Learning. New York: springer.
- Efron, B., Tibshirani, R. J. (1994). An Introduction to the Bootstrap. CRC press.
|
|
Credits:
|
3-1-0-0 (11)
|
|
Prerequisites:
|
MSO205A: Introduction to Probability Theory, MTH207A: Matrix Algebra and Linear Estimation (Module II)
|
|
Objectives:
|
This course covers concepts in various aspects of classical theoretical statistics. Students will be introduced to descriptive statistics, visualizations, frequentist and Bayesian estimation, hypothesis testing. Focus will be on the theoretical underpinnings of concepts.
|
|
Course Contents:
|
- Descriptive Statistics
- Population and sample notions
- Methods of sampling: Simple random sampling with (and without) replacement, stratified sampling
- Types of data: categorical, continuous, ordinal, nominal
- Visualizing (univariate and multivariate): boxplots, histogram, stemleaf plot, bar graph, ogive, scatterplot, side-by-side boxplot, starplot [5 lectures]
- Measures of Central Tendency
- Means (arithmetic, geometric, harmonic), median, mode [1 lecture]
- Measures of Dispersion
- Variance, interquantile range
- Mean absolute deviation, standard deviation
- Skewness, kurtosis, coefficient of variation
- sample rth moment and raw moments [3 lectures]
- Measures of association
- Correlation, Kendall’s τ, Spearman rank correlation [2 lectures]
- Point Estimation
- Statistic, estimators
- Sufficiency, completeness, unbiasedness, UMVUE
- Information inequalities, Cram´er-Rao lower bound
- Methods of estimation: maximum likelihood estimator, method of moments
- Properties of MLE and MoM [11 lectures]
- Testing of Hypothesis
- Null and alternative hypothesis
- simple and composite hypothesis
- size, power
- Neyman-Pearson lemma for simple vs simple and its use for testing composite hypothesis
- UMP test, likelihood ratio tests [10 lectures]
- Confidence Interval
- Pivotal statistics, methods of constructions [3.5 lectures]
- Bayesian statistics
- Basics, point estimation as a decision problem
- Prior dist, Bayes risk, Bayes estimators under losses
- credible sets [4.5 lectures]
|
|
References:
|
- Hogg, R. V., McKean, J., Craig, A. T. (2005). Introduction to Mathematical Statistics. Pearson Education.
- Rohatgi, V. K., Saleh, A. M. E. (2015). An introduction to probabilityand statistics. John Wiley and Sons.
- Casella, G., Berger, R. L. (2021). Statistical inference. Cengage Learning.
|
|
Credits:
|
3-1-0-0 [6] (modular)
|
|
Prerequisites:
|
MSO201A Probability and Statistics or MSO205A Introduction to Probability Theory or equivalent
|
|
Syllabus:
|
- Definition and classification of general stochastic processes [0.5 lecture] • Markov Processes and Markov Chains
- Definition and classification of Markov processes [0.5 lecture]
- Definition of Markov Chains of Order r (focus on Order 1), and corresponding Transition Probability Matrices [1 lecture]
- Examples - Gambler’s Ruin, Random Walk etc. [1 lecture]
- Chapman-Kolmogorov equations, Derivation of higher order transition probabilities from 1-step transition probabilities. [1 lecture]
- Classification of States: [6 lectures]
∗ Accessible, Absorbing and Communicating states
∗ Communication as an equivalence relation
∗ Irreducible Markov Chains
∗ Recurrent and Transient states (focus on the probability of visiting a state infinitely often, through Borel-Cantelli Lemma) ∗ Effect of dimension on a Markov chain: compare through Random Walks on 1, 2 and 3 dimensions
- Finite Markov chains, properties of finite irreducible Markov Chains [1 lecture]
- Periodic States [0.5 lecture]
- Closed sets, Communicating class properties, absorption in closed sets [1 lecture]
- Limiting behaviours: Null and Positive Recurrence, Ergodicity [2.5 lectures]
- Stability of Markov Chains, Limiting distributions, Stationary distributions [5 lectures]
|
|
References:
|
- Samuel Karlin and Howard M Taylor: A First Course in Stochastic Processes, 2ed, Academic Press, 1975.
- Sheldon M Ross: Stochastic Processes, John Wiley and Sons, 1996.
- Etienne Pardoux: Markov Processes and Applications, John Wiley andSons, 2008.
- Achim Klenke: Probability Theory, Springer-Verlag, 2008.
|
|
Syllabus:
|
Pre-requisite: MTH 102, None for M.Sc. 2 yr
Divisibility, Primes, fundamental theorem of arithmetic, Euclidean algorithm, Congruence and modular arithmetic, Chinese remainder theorem, Roots of unity, Quadratic reciprocity, Binary quadratic forms, Some Diophantine equations, Some arithmetic functions, Distribution of prime numbers, Bertrand's postulate, the partition function, Dirichlet Series, Riemann Zeta function.
Reference materials:
-
I. Niven, H. S. Zuckerman and H. L. Montgomery. An Introduction to the Theory of Numbers, Wiley, 1991
-
David M. Burton, Elementary Number Theory. McGraw Hill Education, 2012.
-
K. Ireland, and M. Rosen. A Classical Introduction to Modern Number Theory. GTM-84, Springer, 1990.
-
G. H. Hardy and E. M. Wright. An Introduction to the Theory of Numbers. Oxford University Press, 1960.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 101, None for M.Sc. 2 yr
Real Number system: Completeness property. Countable and Uncountable. Metric Spaces: Metric spaces, Examples: 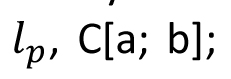 Limit, Open sets, Convergence of a sequence, Closed sets, Continuity. Completeness: Complete metric space, Nested set theorem, Baire category theorem, Applications. Compactness: Totally bounded, Characterizations of compactness, Finite intersection property, Continuous functions on compact sets, Uniform continuity. Connectedness: Characterizations of connectedness, Continuous functions on connected sets, Path connected. Riemann integration: Definition and existence of integral, Fundamental theorem of calculus, Set of measure zero, Cantor set, Characterization of integrable functions. Convergence of sequence and series of functions: Pointwise and uniform convergence of functions, Series of functions, Power series, Dini's theorem, Ascoli's theorem, Continuous function which is nowhere differentiable, Weierstrass approximation theorem. Limit, Open sets, Convergence of a sequence, Closed sets, Continuity. Completeness: Complete metric space, Nested set theorem, Baire category theorem, Applications. Compactness: Totally bounded, Characterizations of compactness, Finite intersection property, Continuous functions on compact sets, Uniform continuity. Connectedness: Characterizations of connectedness, Continuous functions on connected sets, Path connected. Riemann integration: Definition and existence of integral, Fundamental theorem of calculus, Set of measure zero, Cantor set, Characterization of integrable functions. Convergence of sequence and series of functions: Pointwise and uniform convergence of functions, Series of functions, Power series, Dini's theorem, Ascoli's theorem, Continuous function which is nowhere differentiable, Weierstrass approximation theorem.
Reference materials:
-
N. L. Carothers, Real Analysis.
-
R. R. Goldberg, Methods of Real Analysis.
-
W. Rudin, Principles of Mathematical Analysis.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 102, MTH 202 for M.Sc. 2 yr
Some basics of set theory: Relations, Partitions, Functions and sets of functions. Families of sets, Cartesian products of families. Principles of weak and strong mathematical induction and their equivalence. Schroder-Bernstein theorem. Countable and uncountable sets. Cantor's theorem. Classical propositional calculus (PC): Syntax. Valuations and truth tables, Truth functions, Logical equivalence relation. Semantic consequence and satisfiability. Compactness theorem with application. Adequacy of connectives. Normal forms. Applications to Circuit design. Axiomatic approach to PC: soundness, consistency, completeness. Other proof techniques: Sequent calculus, Computer assisted formal proofs: Tableaux. Decidability of PC, Boolean algebras: Order relations. Boolean algebras as partially ordered sets. Atoms, Homomorphism, sub-algebra. Filters. Stone's representation (sketch). Completeness of PC with respect to the class of all Boolean algebras. Classical first order logic (FOL) and first order theories, Syntax. Satisfaction, truth, validity in FOL. Axiomatic approach, soundness. Computer assisted formal proofs: Tableaux. Consistency of FOL and completeness (sketch). Equality. Examples of first order theories with equality. Peano's arithmetic. Zermelo-Fraenkel axioms of Set theory. Axiom of choice, Well-ordering theorem, Zorn's lemma and their equivalence; illustrations of their use. Well-ordering principle and its equivalence with principles of weak and strong induction. Elementary model theory: Compactness theorem, Löwenheim-Skolem theorems. Completeness of first order theories, Isomorphism of models, Categoricity-illustrations through theories such as those of finite Abelian groups, dense linear orders without end points and Peano's arithmetic. Statements of Gödel's incompleteness theorems and un-decidability of FOL.
Reference materials:
-
J. Bridge: Beginning Model Theory: The Completeness Theorem and Some Consequences. Oxford Logic Guides, 1977.
-
I. Chiswell and W. Hodges: Mathematical Logic. Oxford, 2007.
-
R. Cori and D. Lascar: Mathematical Logic, Oxford, 2001.
-
J. Goubalt-Larrecq and J. Mackie: Proof Theory and Automated Deduction, Kluwer, 1997.
-
P. R. Halmos: Naive Set Theory, Springer, 1974.
-
J. Kelly: The Essence of Logic, Pearson, 2011.
-
A. Margaris, First Order Mathematical Logic, Dover, 1990.
|
|
Credits:
|
11
|
|
Credits:
|
3-1-0-0 [11]
|
|
Content:
|
Some Topics in Elementary number theory: Complexity of Computation & Complexity Classes, time estimates of doing arithmetic, divisibility and the euclidean algorithm, prime, finite abelian group, congruences modulo n, the Chinese remainder theorem, computing inverse and huge powers.
Finite fields and quadratic residues: Finite fields, Group of units in finite fields, quadratic residues and reciprocity.
Cryptography: Some simple cryptosystems, enciphering matrices.
Public key: The idea of public key cryptosystem, Choice of the public key, RSA, Attacks on RSA and remedies, discrete log, knapsack, Zero-knowledge protocols and oblivious transfer.
Primality and factoring: The rho method, Fermat factorization and factor bases, the continued fraction method, the quadratic sieve method, pseudoprimes, fermat primality test, Miller-Rabin primality test, Solovay-Strassen primality test, AKS primality test.
Elliptic curves: The definition and basic facts, The group structure on an elliptic curve, Integer factorization using elliptic curves, elliptic curve primality test, elliptic curve cryptosystem, elliptic curves over rational numbers.
|
|
Syllabus:
|
Pre-requisite: MTH 301
Topological spaces; open sets, closed sets, basis, sub-basis, closure, interior and boundary. Subspace topology. Continuous maps, open maps, closed maps, Homeomorphisms. Product Topology. Hausdorff spaces, Countability and separation axioms. Compact spaces and its properties, Locally compact spaces, one point compactification, Tychonoff's Theorem, Statement and Applications of Urysohn Lemma, Tietz extension theorem and Urysohn metrization theorem. Connectedness, path connectedness, components, its properties. Quotient Topology, various type of examples, cone, suspension, surfaces as quotient spaces. Group actions, orbit spaces. (Time permitting: Homotopy, Fundamental group, deformation retract, contractible spaces, simply connected spaces, computation of 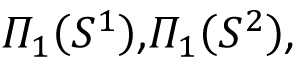 ,, Brouwer fixed point theorem.) ,, Brouwer fixed point theorem.)
Reference materials:
-
J. R. Munkres: Topology: A First Course, Prentice-Hall, 1975.
-
J. Dugundji: Topology, UBS, 1999.
-
M. A. Armstrong: Basic Topology, Springer.
-
G. F. Simmons: Introduction to Topology and Modern Analysis, Tata McGraw-Hill, 1963.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 301
Differentiation: Differentiable functions, Directional derivatives, Composition of differentiable functions and chain rule, Mean value inequalities. Inverse mapping theorem and Implicit mapping theorem. Regular value of differentiable maps, Lagrange multipliers. Higher order derivatives, Taylor's Theorem. Curves: Definition and examples of regular curves in R^2 and R^3. Definition of parametrised curves. Arc length of a regular curve and arc length parametrisation of regular curves. Curvature of plane curves and Frenet-Serret formula for regular space curves. Statement of Green's Theorem. Isoperimetric inequality for plane curves. Surfaces: Three equivalent definition of regular surfaces in R^3. Tangent planes. Differentiable functions on surfaces and differentiable maps between surfaces. Tangent Plane. Derivative of differentiable functions/maps on surfaces. First fundamental form. Local isometries. Gauss map, Weingartent map and second fundamental form. Principal curvatures, Gauss curvature and mean curvature of surfaces. Surfaces of revolution and classification of surfaces of revolution of constant curvature. Umbilic points on surface. Classification of totally umbilical surfaces. Hilbert's theorem on compact surfaces. Geodesics and examples.
Reference materials:
-
Tom M. Apostol: Mathematical Analysis, Narosa Publishing House, India.
-
W. Rudin: Principles of Mathematical Analysis.
-
Spivak: Calculus on manifolds, Springer.
-
A Pressley: Elementary differential geometry, Springer India.
-
M P do Carmo: Differential geometry of curves and surfaces, Prentice Hall.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite(s): MTH 102 / None for M.Sc. 2 yr
Approximations in Scientific computing, Error propagation and amplification, conditioning, stability and accuracy, computer arithmetic mathematical software and libraries, visualization, linear systems- existence and uniqueness, sensitivity and conditioning, Gaussian elimination, special linear systems, iterative methods, nonlinear equations, convergence rates, non-linear equations in one dimension, system of non-linear equations, eigenvalue problems, existence and uniqueness, sensitivity and conditioning, computing eigenvalues and eigenvectors, approximation and interpolation, Hermite and Spline interpolation, piecewise polynomial interpolation, numerical differentiation and integration, Chebyshev differentiation and FFT, Richardson extrapolation.
Reference material(s):
-
M Heath: Scientific Computing - An introductory Survey.
-
Kendall E. Atkinson: An Introduction to Numerical Analysis.
-
S. D. Conte & S. de Boor: Elementary Numerical Analysis: An Algorithmic Approach.
-
J. Stoer and R. Bulirsch: Introduction to Numerical Analysis.
|
|
Credits:
|
10 |
|
Credits:
|
3-1-0-0 [11]
|
|
Prerequisites:
|
This is a compulsory course for 2-year M.Sc (Statistics) students. For all other students, MSO201A or equivalent will be taken as prerequisite.
|
|
Syllabus:
|
- Limits of sequences of sets, σ-field of events. Probability measure, probability space.
- Random variables, induced probability space, probability distribution.Distribution function, decomposition theorem.
- Expectation and moments, inequalities.
- Various modes of convergence of sequences of random variables (in probability, almost surely, in r-th mean). Convergence theorems for expectations of sequences of random variables (monotone convergence theorem, Fatou’s lemma, dominated convergence theorem).
- Characteristic function and its properties, inversion formulae.
- Convergence of sequences of distribution functions, Helly-Bray theorems,convergence of moments.
- Independence of events and random variables, zero one laws.
- Convergence of series of independent random variables, Kolmogorov inequality, Kolmogorov three-series criterion.
- Khintchin’s weak law of large numbers, Kolmogorov strong law of largenumbers. Central limit theorems of Lindeberg-Levy, Liapounov and Lindeberg- Feller.
|
|
References:
|
- L.Chung: A Course in Probability Theory, Third Edition, AcademicPress, 2001.
- R.Bhat: Modern Probability Theory, Third Edition, New Age International (P) Ltd, 2004.
- Lo´eve: Probability Theory-I, Graduate Text in Mathematics, FourthEdition, Springer, 1977.
|
|
Credits:
|
1-0-2-0 (5)
|
|
Prerequisites:
|
MTH208A, MTH209A.
|
|
Objectives:
|
To provide students an exposure to real data problems and give hands-on experience of analyzing big-to-small data sets. Students will use the concepts learned in various statistics and data science courses to analyze the data sets given to them. In addition to model building and prediction, focus will be on statistical communication via reports (which includes supporting codes) and presentations.
|
|
Syllabus:
|
The course covers analysis of a collection of datasets obtained from a variety of disciplines and applications. Every week, the goal will be to build a model and/or a prediction scheme to answer the questions pertaining to the field of application. Writing weekly reports and/or presentations will be an integral part of the course.
|
|
References:
|
- James, G., Witten, D., Hastie, T., Tibshirani, R. (2013). An Introductionto Statistical Learning. New York: Springer.
- Shumway, R. H., Stoffer, D. S. (2000). Time Series Analysis and Its Applications. New York: Springer.
- Everitt, B., Fienberg, S., Olkin, I., Casella, G. (2005). An R and S-PLUSCompanion to Multivariate Analysis. London: Springer.
- Marin, J. M., Robert, C. P. (2007). Bayesian Core: A Practical Approachto Computational Bayesian Statistics. New York: Springer.
- Gelman, A., Carlin, J. B., Stern, H. S., Rubin, D. B. (1995). BayesianData Analysis. Chapman and Hall/CRC.
- Christensen, R., Johnson, W., Branscum, A., Hanson, T. E. (2010). BayesianIdeas and Data Analysis: An Introduction for Scientists and Statisticians. CRC press.
|
|
Credits:
|
3-1-0-0 [6] (modular)
|
|
Prerequisites:
|
MSO201A Probability and Statistics or MSO205A Introduction to Probability Theory or equivalent
|
|
Syllabus:
|
- Continuous time Stochastic Processes (focus on Counting process), Kolmogorov Consistency/Existence Theorem (statement only) [0.5 lecture]
- Poisson Process (PP) [7.5 lectures]
- Definition of a PP as a counting process
- Alternative definition of a PP
- Inter-arrival and Waiting times for a PP, Coupon Collector’s problem
- Order Statistics and PP
- Non-homogeneous PP, properties involving the arrival times
- Compound PP
- Continuous time Markov Chains (Discrete State space) or Jump Markov Processes [7 lectures]
- Definition (focus on homogeneous Markov Chains)
- Examples
∗Birth and Death processes
∗ Poisson Process as a Pure Birth process
∗ M/M/c queues
∗ Linear growth Models with immigration
∗ Yule Process
- Transition Probability function, Chapman-Kolmogorov equations (forward and backward)
- Limiting probabilities (may be an overview only, heuristic proof may be given with some motivation using the first module)
- Brownian Motion (BM) [2 lectures]
- Definition of a BM, BM as a Markov process
- Gaussian processes
- Properties of a BM
∗ Covariance function, Invariance properties
∗ Path properties - using the Kolmogorov Continuity Theorem
(statement only)
- Special topics (one of the following two topics to be covered) [3 lectures]
- Topic 1: Processes related to Brownian motion
∗ Brownian bridge, Application of Brownian bridge in the study of empirical processes, Donsker’s Invariance Principle (statement only) ∗ Stopping times, Hitting times, Strong Markov Property, Arc-Sine laws
∗ Variants of BM: involving absorption and reflection, Geometric BM, Integrated BM, involving drift – Topic 2: Branching processes
∗ A little history of branching processes. The Galton-Watson Branching Processes (GWP). Probability generating function of GWP. Moment generating functions and moment calculations ∗ Sub-critical, critical and super-critical scenario and the probability of extinction. Examples. Introduction to Continuous time Markov Branching Processes.
∗ Examples of Continuous time Markov Branching Processes – revisit to Yule Process or Binary Fission, Birth & Death Process. Generating functions. Sub-critical, critical and super-critical scenarios.
|
|
References:
|
- Samuel Karlin and Howard M Taylor: A First Course in Stochastic Processes, 2ed, Academic Press, 1975.
- Sheldon M Ross: Stochastic Processes, John Wiley and Sons, 1996.
- Etienne Pardoux: Markov Processes and Applications, John Wiley andSons, 2008.
- Achim Klenke: Probability Theory, Springer-Verlag, 2008.
- B. Athreya and Peter Ney: Branching Processes, Springer-Verlag BerlinHeidelberg, New York 1972.
- B. Athreya and S. N. Lahiri: Measure Theory and Probability Theory,Springer, 2006.
|
|
Credits:
|
3-0-1-0 (10)
|
|
Prerequisites:
|
MTH211A or MTH418A
|
|
Objectives:
|
The objective of the course is to impart necessary knowledge about theoretical foundations of multivariate distribution theory, with special emphasis on Multivariate Gaussian distribution, statistical inferential aspects related to random sampling from multivariate populations and to learn various important applied multivariate data analysis tools and techniques, with a view to understand the mathematical derivation and justification of these methods and further to implement them for solving real life problems.
|
|
Course Contents:
|
- Basic properties of random vector
CDF and PDF of random vectors – Moments – Characteristics functions Orthogonal and Polar transformations Generalization of univariate distribution (Multinomial, Dirichlet). [3 Lectures]
- Normal Distribution Theory
Normal data matrix (NDM): characterization and properties Linear forms – Transformation of NDMs Wishart Distribution The Hotelling’s T2 Distribution [9 lectures]
- Estimation and Testing
Maximum likelihood estimation Likelihood ratio test – Union intersection test Simultaneous confidence intervals. [6 lectures]
- Multivariate Analysis of Variance (MANOVA)
Formulation of multivariate one-way classification Likelihood ratio principle [3 lectures]
- Principal Component Analysis
Principal components – Sampling properties of principal components – Principal component projections. [3 lectures]
- Factor Analysis
The factor model – Principal factor analysis – Maximum likelihood factor analysis – Goodness of fit – rotation of factors – factor scores [4 lectures]
- Canonical correlation analysis
Population and sample canonical correlation vectors, variables and coefficients and their properties. [3 lectures]
- Discrimination Analysis
Fisher’s LDA -QDA – Probabilities of misclassification [3 Lectures]
- Cluster Analysis
Distances and similarities – Hierarchical methods – K-means method [3 Lectures]
- Project presentations [5 Lectures]
|
|
References:
|
- Mardia, K. V., Bibby, J. M., Kent, J. T. (1979). Multivariate Analysis.United Kingdom: Academic Press.
- Johnson, R. A., Wichern, D. W. (2019). Applied Multivariate StatisticalAnalysis. United Kingdom: Pearson.
- Muirhead, R. J. (2009). Aspects of Multivariate Statistical Theory. Germany: Wiley.
- Anderson, T. W. (2003). An Introduction to Multivariate Statistical Analysis. United Kingdom: Wiley.
- Hastie, T., Friedman, J., Tibshirani, R. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Germany: Springer New York.
- Brenner, D., Bilodeau, M. (1999). Theory of Multivariate Statistics. Germany: Springer.
- Johnson, R. A., Wichern, D. W. (2019). Applied Multivariate Statistical Analysis. United Kingdom: Pearson
|
|
Credits:
|
0–0–0–9 (9)
|
|
Prerequisites:
|
MTH211A (Only for BS (Statistics and Data Science) students.)
|
|
Objectives:
|
The course allows students to do internships in Statistics and Data Science under the guidance of a departmental supervisor. This course should allow students to get exposed to real world problems and use the tools learned in the Statistics and Data Science BS program. The grading scheme will be S/X.
This course runs under an appropriate Memorandum of Understanding (MoU) between Indian Institute of Technology Kanpur and the host organization under which a student plans to undertake the internship. The process of enrolling in an internship, the duration and other relevant terms and conditions shall be as set out in the MoU.
|
|
Credits:
|
0–0–0–9 (9)
|
|
Prerequisites:
|
MTH211A (Only for BS (Statistics and Data Science) students.)
|
|
Objectives:
|
The course allows students to do internships in Statistics and Data Science under the guidance of a departmental supervisor. This course should allow students to get exposed to real world problems and use the tools learned in the Statistics and Data Science BS program. The grading scheme will be S/X.
This course runs under an appropriate Memorandum of Understanding (MoU) between Indian Institute of Technology Kanpur and the host organization under which a student plans to undertake the internship. The process of enrolling in an internship, the duration and other relevant terms and conditions shall be as set out in the MoU.
|
|
Credits:
|
0–0–0–9 (9)
|
|
Prerequisites:
|
MTH211A (Only for BS (Statistics and Data Science) students.)
|
|
Objectives:
|
The course allows students to do internships in Statistics and Data Science under the guidance of a departmental supervisor. This course should allow students to get exposed to real world problems and use the tools learned in the Statistics and Data Science BS program. The grading scheme will be S/X.
This course runs under an appropriate Memorandum of Understanding (MoU) between Indian Institute of Technology Kanpur and the host organization under which a student plans to undertake the internship. The process of enrolling in an internship, the duration and other relevant terms and conditions shall be as set out in the MoU.
|
|
Credits:
|
0–0–0–9 (9)
|
|
Prerequisites:
|
MTH211A (Only for BS (Statistics and Data Science) students.)
|
|
Objectives:
|
The course allows students to do internships in Statistics and Data Science under the guidance of a departmental supervisor. This course should allow students to get exposed to real world problems and use the tools learned in the Statistics and Data Science BS program. The grading scheme will be S/X.
This course runs under an appropriate Memorandum of Understanding (MoU) between Indian Institute of Technology Kanpur and the host organization under which a student plans to undertake the internship. The process of enrolling in an internship, the duration and other relevant terms and conditions shall be as set out in the MoU.
|
|
Credits:
|
0–0–0–9 (9)
|
|
Prerequisites:
|
MTH211A (Only for BS (Statistics and Data Science) students.)
|
|
Objectives:
|
The course allows students to do internships in Statistics and Data Science under the guidance of a departmental supervisor. This course should allow students to get exposed to real world problems and use the tools learned in the Statistics and Data Science BS program. The grading scheme will be S/X.
This course runs under an appropriate Memorandum of Understanding (MoU) between Indian Institute of Technology Kanpur and the host organization under which a student plans to undertake the internship. The process of enrolling in an internship, the duration and other relevant terms and conditions shall be as set out in the MoU.
|
|
Syllabus:
|
Pre-requisite: None (Only for BS students)
|
|
Credits:
|
4
|
|
Syllabus:
|
Pre-requisite: None (Only for BS students)
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: None (Only for BS students)
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: None (Only for BS students)
|
|
Credits:
|
4
|
|
Syllabus:
|
Pre-requisite: None (Only for BS students)
|
|
Credits:
|
5 |
|
Syllabus:
|
Pre-requisite: MTH302/Consent of Instructor
Regular languages, Deterministic and non-deterministic finite automata, Closure properties, Languages that are and are not regular, State minimization in deterministic finite automata. Context-free languages, Closure properties, Parse-trees, Languages that are and are not Context-free, Pushdown automata. Turing machines, Turing computability, Church-Turing thesis, Halting problem, Some undecidable problems. Computational complexity, Classes P and NP, Completeness, Examples of NP complete problems.
Reference materials:
-
H. R. Lewis and C. H. Papadimitriou: Elements of the Theory of Computation, Prentice Hall, 1998.
-
J. E. Hopcroft, R. Motwani, J. D. Ullman: Introduction to Automata Theory, Languages and Computation, Pearson Education, 2001.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH301/Consent of Instructor
Preliminaries to Complex analysis: Basic properties: convergence, compactness, connectedness; continuous functions, Holomorphic functions, power series, integration along curves and properties. Cauchy's theorem and its application: Goursat's theorem, local existence of primitives and Cauchy's theorem in a disc, evaluation of some integrals, Cauchy's integral formulas, Morera's theorem, sequence of holomorphic functions. Meromorphic functions and the Logarithm: Zeros and poles, the residue formula, singularities and meromorphic functions, the argument principle and applications, open mapping theorem, maximum modulus principle, Picard's little theorem, the complex logarithms, harmonic functions. Conformal mappings: Conformal equivalence: the disc and the upper half-plane; The Dirichlet problem in a strip, Schwartz lemma, automorphism of disc, automorphism of the upper half-plane, Montel Theorem, Riemann mapping theorem.
Reference materials:
-
L. V. Ahlfors: Complex analysis, McGraw-Hill international editions.
-
John B. Conway: Functions of one complex variable, Springer International Student Edition.
-
R. Narasimhan, Y. Nievergelt: Complex analysis in one variable, Birkhauser.
-
Walter Rudin: Real and Complex analysis, McGraw-Hill international editions.
-
E. M. Stein and R. Shakarchi: Complex Analysis, Princeton University Press.
-
T. Gamelin: Complex analysis, Springer.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH301/ Instructor's Consent
Lebesgue measure on 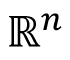 : Introduction, outer measure, measurable sets, Lebesgue measure, regularity properties, non-measurable sets, measurable functions, Egorov's theorem, Lusin's theorem, Lebesgue Integration: Simple functions, Lebesgue integral of a bounded function over a set of finite measure, bounded convergence theorem, Integral of non-negative measurable functions, Fatou's lemma, monotone convergence theorem, general Lebesgue integral, Dominated convergence theorem, change of variable formula, Fubini's theorem. : Introduction, outer measure, measurable sets, Lebesgue measure, regularity properties, non-measurable sets, measurable functions, Egorov's theorem, Lusin's theorem, Lebesgue Integration: Simple functions, Lebesgue integral of a bounded function over a set of finite measure, bounded convergence theorem, Integral of non-negative measurable functions, Fatou's lemma, monotone convergence theorem, general Lebesgue integral, Dominated convergence theorem, change of variable formula, Fubini's theorem. 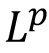 spaces: The Minkowski's inequality and Hölder's inequality, completeness of spaces: The Minkowski's inequality and Hölder's inequality, completeness of 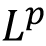 and denseness results in and denseness results in 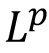 Differentiation and Integration: Functions of bounded variation, differentiation of an integral, Absolute continuity. Differentiation and Integration: Functions of bounded variation, differentiation of an integral, Absolute continuity.
Reference materials:
-
G. de Barra: Measure theory and integration, Harwood Publishing Limited, Chichester, 2003.
-
E. M. Stein and R. Shakarchi: Real analysis, measure theory, integration and Hilbert spaces, Princeton University Press.
-
Walter Rudin: Real and Complex analysis, McGraw-Hill international editions.
-
H. L. Royden and P. M. Fitzpatric, Real Analysis, 4th ed, Pearson, 2015.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH301/Consent of Instructor
Banach spaces, Riesz Lemma (On compactness of the unit ball in a normed linear space), Bounded linear maps on finite and infinite-dimensional normed linear spaces: Hahn Banach Theorem (geometric and extension forms), characterization of finite-dimensional normed linear spaces, Fundamental theorems on Banach spaces-Uniform Boundedness Principle, Closed Graph Theorem, Open Mapping Theorem. Dual spaces of some classical spaces, e.g., 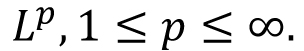 Weak and Weak* convergence Banach Alaoglu Theorem. Hilbert spaces: Gram-Schmidt orthonormalization process, Bessel's inequality, orthonormal basis, Riesz Representation Theorem-Dual of a Hilbert space, Bounded operators on a Hilbert space: Adjoint of an operator, orthogonal projections, self-adjoint, normal and unitary operators Introduction to Banach Algebras-Spectrum of an operator, Spectral Theorem for compact self-adjoint operators, Spectral Theorem for self-adjoint operators (optional) Weak and Weak* convergence Banach Alaoglu Theorem. Hilbert spaces: Gram-Schmidt orthonormalization process, Bessel's inequality, orthonormal basis, Riesz Representation Theorem-Dual of a Hilbert space, Bounded operators on a Hilbert space: Adjoint of an operator, orthogonal projections, self-adjoint, normal and unitary operators Introduction to Banach Algebras-Spectrum of an operator, Spectral Theorem for compact self-adjoint operators, Spectral Theorem for self-adjoint operators (optional)
Reference materials:
-
J. B. Conway: A First Course in Functional Analysis
-
Walter Rudin: Functional Analysis
-
Rajendra Bhatia: Notes on Functional Analysis
-
B. V. Limaye: Functional Analysis
-
E. Kreyszig, Introductory Functional Analysis with Applications, Wiley, 2015.
|
|
Credits:
|
11
|
|
Syllabus:
|
Course objective: The aim of the course is to develop programming skills using the fundamental and basics of C language. It also describes the uses of pointers, arrays, structures, linked lists etc in a C program.
Course Contents:
- Introduction
- Basic concepts: Machines, Operating systems
- Introduction to C language: Program design, Writing and running a C program
- Data types and variables
- Operators and their precedence
- Flow control: Relational and logical operators, Conditionals statements, Looping statements
- Arrays, pointers and strings
- Functions: Passing data to functions, Passing addresses to functions
- Data structures: Structures and unions, Linked lists, Stacks, Queues, Binary trees
- Input/Output management.
References:
- A Book on C - A Kelley and I Pohl
- Programming in ANSI C - E Balagurusamy
- The C Programming Language - B W Kernighan an D M Ritchie
|
|
Credits:
|
2-1-1-0 [9]
|
Credits
3-1-0-0 (11)
Prerequisites
MSO201, None for M.Sc. 2 yr Stats
Objectives
The course provides an introduction to the definition and classification of general stochastic processes. For Markov chains, we discuss the definition, transition probability matrices, classification of states, limiting properties. We broadly discuss two types of Markov chains with discrete state space, namely, Poisson process, and birth and death processes. We then discuss a gentle introduction to the Renewal Process. Here we discuss renewal equation, mean renewal time, and stopping time. Finally, we also discuss Markov Process with Continuous State Space, where we introduce the Brownian motion.
Course Contents
- Definition and classification of general stochastic processes
- Markov Chains
- i. Definition ii. Transition probability matrices iii. Classification of states iv. Limiting properties
- Markov Chains with Discrete State Space
- Poisson processii. Birth and death processes
- Renewal Process
- Renewal equationii. Mean renewal time iii. Stopping time
- Markov Process with Continuous State Space
- Introduction to Brownian motion
References
- Sheldon M Ross: Stochastic Processes, John Wiley and Sons, 1996.
- S Karlin and H M Taylor: A First Course in Stochastic Processes, Academic Press, 1975.
Credits
3-1-0-0 (11)
Prerequisites
MSO201A: Probability and Statistics, consent of the instructor.
Objectives Syllabus
Review of finite-dimensional vector spaces (Null space and nullity), Linear dependence and independence, Matrix algebra, Rank of a Matrix, Inverse of a nonsingular matrix. Hermite canonical forms, Generalized inverses, Moore-Penrose inverse, solution of linear equations, Projection and orthogonal projection matrices, Idempotent matrices. Real quadratic forms, reduction of pair of real symmetric matrices, Singular value decomposition. Extrema of a quadratic forms, Vector and matrix differentiation. Least squares theory and Gauss-Markov theorem, Cochran’s theorem and distribution of quadratic forms, test of single linear hypothesis and more than one hypothesis, ANOVA table, Confidence interval and regions, Power of F-test. Multiple comparisons and simultaneous confidence intervals.
References
- B. Bapat: Linear Algebra and Linear Models, Springer, London.
- David A. Herville: Matrix Algebra from a Statistician’s Perspective, SpringerVerlag, New York.
- R. Rao and P. Bhimasankaram: Linear Algebra (Texts and Readingsin Mathematics), Hindustan Book Agency.
- Gilbert Strang: Linear Algebra and its Applications, Cengage Learning.
- Debasis Sengupta and S. R. Jammalamadaka: Linear Models: An Integrated Approach, World Scientific.
|
Syllabus:
|
Pre-requisite: MSO 201, None for M.Sc. 2 yr Stats
Simple and multiple linear regression, Polynomial regression and orthogonal polynomials, Test of significance and confidence intervals for parameters. Residuals and their analysis for test of departure from the assumptions such as fitness of model, normality, homogeneity of variances, detection of outliers, Influential observations, Power transformation of dependent and independent variables. Problem of multi-collinearity, ridge regression and principal component regression, subset selection of explanatory variables, Mallow's Cp statistic. Nonlinear regression, different methods for estimation (Least squares and Maximum likelihood), Asymptotic properties of estimators. Generalized Linear Models (GLIM), Analysis of binary and grouped data using logistic and log-linear models.
Reference materials:
-
Douglas C. Montgomery, Elizabeth A. Peck, G. Geoffrey Vining: Introduction to Linear Regression Analysis, Wiley, Low price Indian edition is available.
-
Norman R. Draper, Harry Smith: Applied Regression Analysis, Low price Indian edition is available.
-
C.R. Rao, H. Toutenburg, Shalabh, and C. Heumann: Linear Models and Generalizations - Least Squares and Alternatives, Springer, 2008.
-
John F. Monahan: A Primer on Linear Models, CRC Press, 2008.
-
Andre I. Khuri: Linear Model Methodology, CRC Press, 2010.
-
H.D. Vinod and Aman Ullah: Recent advances in regression methods, Marcel Dekker.
|
|
Credits:
|
11
|
Credits
3-1-0-0 (11)
Prerequisites
MSO201, None for M.Sc. 2 yr Stats
Objectives
The course begins with a gentle introduction to the exponential family of distributions. Several desired properties of the estimators like sufficiency, completeness, unbiasedness, etc. are subsequently discussed and related theoretical results are also demonstrated through examples. Further, different approaches for parameter estimation like the method of moments, maximum likelihood estimation, minimum mean square estimation, etc. are discussed. Subsequently, some basic concepts regarding statistical hypotheses testing are discussed. Here we cover ideas like simple and composite hypothesis, critical regions, Type-I and Type-II errors, and size and power of a test. Some optimal statistical hypothesis testing procedures like the most powerful test, uniformly most powerful test, unbiased test, monotone likelihood ratio test, etc. are discussed. Further, as a special case, the hypothesis tests are discussed for the exponential family case, where we discuss both the single-parameter and multi-parameter settings.
Course Contents
- Exponential families
- Canonical form iii. Full rank
- Sufficiency
- Neyman Fisher factorization criterionii. Minimal sufficiency iii. Ancillary statistic
- Completeness
- Completeness of family of distributionsii. Completeness of statistic iii. Basu’s theorem and its uses iv. Rao-Blackwell theorem and its implications
- Unbiasedness
- Basic concepts ii. Locally minimum variance unbiased estimatoriii. Uniformly minimum variance unbiased estimator iv. Lehmann- Scheffe’s theorem and its importance
- Methods for finding UMVUE
- Method of solvingii. Rao-Blackwellization iii. Non-parametric families and Hoeffding’s U-statistic
- Information inequality and lower bounds- Hammersley-Chapman- Robbins inequality
- Fisher informationvi. Cramer-Rao lower bond vii. Information inequality for multi-parameter case-information matrix viii. s-parameter exponential family ix. Bhattacharya system of lower bounds
- Methods of estimation
- MOME iii. MinMSE
- Basic concepts in statistical hypotheses testing
- Simple and composite hypothesis ii. Critical regionsiii. Type-I and Type-II errors iv. Size and power of a test
- Neyman-Pearson lemma and its applications
- Type of optimum tests and their construction using NP lemma
- Most powerful testii. Uniformly most powerful test iii. Unbiased test and uniformly most unbiased test iv. Monotone Likelihood ratio and testing with MLR property
- Testing in one-parameter exponential families
- One-sided hypothesisii. UMP and UMPU tests for different two-sided hypothesis
- Testing in multi-parameter exponential families
- Tests with Neyman structure, UMP and UMPU similar size-testsii. Likelihood Ratio test
- Confidence intervals
- Pivotal functionsii. Shortest expected length confidence interval iii. UMA and UMAU confidence intervals
References
- John Rice: Mathematical Statistics and Data Analysis, 3rd edition
- Jun Shao: Mathematical Statistics, 2nd edition
- George Casella and Roger Berger: Statistical Inference, 2nd edition
|
Syllabus:
|
Pre-requisite: MTH 102 / Instructor's consent
Introduction to ODE; Existence and uniqueness of solution; Continuity and differentiability of solution w.r.t. initial condition and parameters; General theory of linear differential equations; Methods of solving non-homogeneous linear equations; Cauchy-Euler equation; Linear equations with periodic coefficients; System of linear differential equations; Stability theory for system of linear differential equations; Strum-Liouville boundary value problems, Oscillation theory; Green's function.
Reference materials:
-
Martin Brown, Differential Equations and Their Applications, Springer, 1992.
-
S. L. Ross, Introduction to Ordinary Differential Equations, Wiley, 1980.
-
Deo, Lakshmikantham, V Raghavendra, Textbook of Ordinary Differential Equations, Tata McGraw Hill, 1997.
-
C. Y. Lin, Theory and Examples of Ordinary Differential Equations, World Scientific, 2011.
|
|
Credits:
|
11
|
Credits 3-0-1-0 (10)
Prerequisites: MTH418A/MTH211A, MTH209A, or Instructor’s consent
Objectives: The proposed course is intended to be a masters’ level course on Bayesian inference and Bayesian computational techniques.
Course Contents:
|
S. No.
|
Broad Title
|
Topics
|
No. of Lectures
|
|
1.
|
A brief review of probability theory
|
Univariate probability distributions (one lecture), multivariate probability distributions (one lecture), conditional distributions (one lecture)
|
3
|
|
2
|
Introduction to Bayes
|
Bayes’ theorem and Bayesian learning (one lecture), Frequentist versus Bayesian (one lecture), problem set discussion (one lecture)
|
3
|
|
3
|
Posterior summarization
|
Univariate posterior summarization (one lecture), multivariate posterior summarization (one lecture), posterior predictive distribution (one lecture), problem set discussion (one lecture)
|
4
|
|
4
|
Conjugate priors
|
Importance of conjugate priors, derivation of the posteriors for a few univariate and multivariate discrete distributions in case of conjugate priors (one lecture), derivation of the posteriors for a few univariate continuous distributions in case of conjugate priors (one lecture), derivation of the posteriors for univariate and multivariate normal distribution in case of conjugate priors (one lecture)
|
3
|
|
5
|
Prior elicitation and objective priors
|
Prior elicitation, mixture priors, and Jeffreys’ priors (one lecture), other objective priors (one lecture), problem set discussion (one lecture)
|
3
|
|
6
|
Bayesian Computations
|
Deterministic computations (one lecture), Gibbs sampling (one lecture), Metropolis-Hastings sampling (one lecture), MCMC convergence diagnostics (one lecture)
|
4
|
|
7
|
Essential softwares
|
R essentials for Bayesian computing (one lecture), JAGS essentials for Bayesian computing (one lecture)
|
2
|
|
8
|
Bayesian linear models
|
Bayesian hypothesis testing, one-sample and two-sample t-tests (one lecture), Bayesian linear regression (BLR) including Bayesian LASSO (one lecture), Implementation of BLR using R-JAGS (one lecture), Bayesian generalized linear models (GLMs) and random-effects models (REMs) (one lecture), Implementation of Bayesian GLMs and REMs using R-JAGS (one lecture), Nonparametric Bayesian regression with R-JAGS illustrations (one lecture)
|
6
|
|
9
|
Bayesian model comparison
|
Bayes factor, Stochastic search variable selection, Bayesian model averaging (one lecture), Crossvalidation (CV), K-fold crossvalidation (K-CV), Some information criteria including DIC and WAIC (one lecture), R-JAGS implementation of CV, K-CV, DIC, and WAIC (one lecture), Posterior predictive checks (one lecture)
|
3
|
|
10
|
Bayesian hierarchical models
|
Building a hierarchical model through layers and its analogy with Directed acyclic graphs (one lecture), Missing data handling in Bayesian models (one lecture)
|
2
|
|
11
|
Case study demonstration
|
Illustation of Bayesian hierarchical models for analyzing real datasets (two lectures)
|
2
|
|
12
|
Big data
|
Case study demonstration (one lecture), Issues with sampling, selection bias and measurement error (one lecture)
|
2
|
|
13
|
Frequentist properties of Bayesian methods
|
Decision theory and Bias-variance tradeoff (one lecture), Asymptotics and simulation studies (one lecture)
|
2
|
Contents of labs:
|
S. No.
|
Broad Title
|
Topics
|
No. of Lectures
|
|
1.
|
Probability distributions in R
|
Univariate and multivariate probability distributions-related functions and additional R packages (one lab)
|
1
|
|
2
|
Introduction to Bayes using R
|
Implementation of simple Bayesian learning examples using R (one lab)
|
1
|
|
3
|
Posterior summarization using R
|
Univariate and multivariate posterior summarization and evaluating posterior predictive distributions using simulation and numerical integration in R (one lab)
|
1
|
|
4
|
Conjugate priors using R: Part 1
|
Examples of the posteriors for a few univariate distributions in case of conjugate priors (one lab)
|
1
|
|
5
|
Conjugate priors using R: Part 2
|
Examples of the posteriors for a few multivariate distributions in case of conjugate priors (one lab)
|
1
|
|
6
|
Objective priors using R
|
Summarizing posterior distributions in case of objective priors, prior elicitation (one lab)
|
1
|
|
7
|
Deterministic computations using R
|
Numerical integration, Gaussian approximation of the posterior distribution and related computations using R (one lab)
|
1
|
|
8
|
Gibbs sampling using R
|
Examples of Gibbs sampling using R (one lab)
|
1
|
|
9
|
Metropolis-Hastinsg sampling using R
|
Examples of Metropolis-Hastinsg sampling using R (one lab)
|
1
|
|
10
|
JAGS implementations
|
Implementation of the same examples using JAGS (one lab)
|
1
|
|
11
|
MCMC convergence diagnostics
|
MCMC convergence diagnostics using R-JAGS (one lab)
|
1
|
|
12
|
Model comparison
|
K-CV, DIC, and WAIC (one lab)
|
1
|
|
13
|
Hierarchical models
|
Implementation of hierarchical models using R-JAGS
|
1
|
Recommended Books:
- Bayesian Statistical Methods by Brian J. Reich, Sujit K. Ghosh. Published in 2019, by Chapman and Hall/CRC (this book will be mainly followed).
- Bayesian Essentials with R by Jean-Michel Marin and Christian P. Robert. Published in 2014, by Springer.
- John K Kruschke, Doing Bayesian Data Analysis, 2nd Ed., Elsevier, 2015.
- Richard McElreath, Statistical Rethinking: A Bayesian Course with Examples in R and Stan, 2nd Ed., CRC Press, 2020.
- Bayesian Data Analysis by Andrew Gelman, John Carlin, Hal Stern, David Dunson, Aki Vehtari, and Donald Rubin. Published in 2013 by Chapman and Hall/CRC. For non-commercial purposes, a free electronic copy can be downloaded from http://www.stat.columbia.edu/~gelman/book/.
- A First Course in Bayesian Statistical Methods by Peter D. Hoff. Published in 2009, by Springer.
- An Introduction to Bayesian Analysis by Jayanta K. Ghosh, Mohan Delampady, Tapas Samanta. Published in 2006 by Springer (printed Indian edition available).
|
Syllabus:
|
Pre-requisite: MTH 421 / Instructor's consent
Introduction to PDEs, First order quasilinear and nonlinear equations; Higher order equations and classifications; Solution of wave equations, Duhamel's principle and applications; Existence and uniqueness of solutions; BVPs for Laplace's and Poisson's equations, Green's function, Maximum principle for the Laplace equation; Heat equation, Maximum principle for the heat equation, Uniqueness of solutions of IVPs for heat conduction equation.
Reference materials:
-
Robert C. McOwen: Partial Differential Equations, Pearson Education Inc.
-
Alen Jeffrey: Applied Partial Differential Equations, Academic Press
-
Ervin Kreyszig: Advanced Engineering Mathematics, John Wiley & Sons
-
T. Amarnath, An Elementary Course in Partial Differential Equations, Narosa Publications
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 102/None for M.Sc. 2 yr
What is a model? What is Mathematical modelling? Role of Mathematics in problem solving; Transformation of Physical model to Mathematical model with some illustrations of real world problems; Mathematical formulation, Dimensional analysis, Scaling, Sensitivity analysis, Validation, Simulation, Some case studies with analysis (such as exponential growth and decay models, population models, Traffic flow models, Optimization models).
Reference material(s):
-
D. N. P. Murthy, N. W. Page and E. Y. Rodin: Mathematical Modelling: A Tool for Problem Solving in Engineering, Physical, Biological and Social Sciences, Pergamon 1990.
-
Clive L. Dyne: Principles of Mathematical Modeling, Academic Press, 2004.
-
R. llner, C. Sean Bohun, S. McCollum and T. van Roode: Mathematical Modeling: A case study approach, AMS 2004.
|
|
Credits:
|
11
|
Credits
4-1-0-0 (11)
Prerequisites
MTH421A
Objectives
This is one of the main courses for students who seek knowledge in the areas of Applied Mathematics. It is aimed to equip the students with the fundamental theory and tools based on the theory of integral theorems in Euclidean spaces. These integral theorems include famous Green’s theorem, Gauss’s divergence theorem and Stokes’s theorem and its applications. The second part of the course deals with the Fourier series and integrals and its applications. The third and the final part of the course covers the theory and applications of the calculus of variations. To make the course material self sufficient, a brief introduction to vectors is also included at the beginning.
Course Contents
Unit I: Vector Algebra and Vector Calculus Vector Algebra: Vectors in 2 and 3 dimensional Spaces, Inner Product (Dot Product) of vectors, Vector Product (Cross Product) of vectors, Scalar and vector Functions and Their Fields. Vector Calculus: Derivatives of scalar and vector functions, Curves, Arc Length, Curvature, Torsion, Functions of Several Variables, Gradient of a Scalar Field, Directional Derivative, Divergence of a Vector Field, Curl of a Vector Field. Unit II:Vector Integral Calculus. Integral Theorems Line Integrals, Path Independence of Line Integrals, Double Integrals, Greens Theorem in the Plane, Surfaces and their representations, Surface Integrals, Triple Integrals, Divergence Theorem of Gauss, Further Applications of the Divergence Theorem, Stokes’s Theorem.
Unit III: Fourier Series and Fourier Integrals Trigonometric Series, Arbitrary Period, Even and Odd Functions, Half-Range Expansions, Forced Oscillations, Approximation by Trigonometric Polynomials, Sturm-Liouville Problems (SLPs). Orthogonal Functions, Orthogonal Series. Generalized Fourier Series, Fourier Integral, Fourier Cosine and Sine Transforms, Fourier Transform, Convolution Theorem.
Unit IV:The Theory of Calculus of Variations: Functionals. Some Simple Variational Problems, function Spaces, The Variation of a functional, A Necessary Condition for an Extremum, Euler’s Equation, The Case of Several Variables, A Simple Variable End Point Problem, The Variational problems in Parametric form, Functional Depending on Higher order Derivatives, Invariance of Euler’s Equation. The Fixed End Point Problem for n Unknown Functions, Functionals Depending on Higher-Order Derivatives, Variational Problems with Subsidiary Conditions.
References
[CB] Ruel V. Churchill and James Brown, Fourier Series and Boundary Value Problems, McGraw-Hill, 1985.
[E] L. Elsgolts, Differential Equations and the Calculus of Variations, Mir Publishers, Moscow, English Translation, 1977.
[EK] Ervin Kreyszig, Herbert Kreyszig, Edward J. Norminton: Advanced Engineering Mathematics, John Wiley & Sons, Inc., 2011.
[S] G.F. Simmons, Differential Equations with Historical Notes, CRC Press, 2017.
|
Syllabus:
|
Pre-requisite(s): MTH 308
Linear least squares problems, existence and uniqueness, sensitivity and conditioning, orthogonalization methods, SVD, Optimization, existence and uniqueness, sensitivity and conditioning, Newton's method, Unconstrained Optimization, Steepest descent, Conjugate gradient method, Constrained optimization (optional), Numerical solution to ODE, IVP: Euler's method, One step and linear multistep methods, Stiff differential equations, boundary value problems, Numerical solution to PDEs, review of second order PDEs: hyerbolic, parabolic and elliptic PDEs, Time dependent problems, Time independent problems
Reference material(s):
-
Michael Heath: Scientific Computing - An Introductory Survey.
-
K. E. Atkinson: An Introduction to Numerical Analysis.
-
S. D. Conte and C. de Boor: Elementary Numerical Analysis: An Algorithmic Approach.
-
J. Stoer and R. Bulirsch: Introduction to Numerical Analysis.
|
|
Credits:
|
10
|
Credits
3-1-0-0 [11]
Prerequisites
None for 2-year M.Sc. students
Syllabus
- Limits of sequences of sets, sigma-field of events. Probability measure, andprobability space. Random variables, induced probability space and probability distribution. Distribution function of univariate random variables, decomposition theorem. Expectation, moments and moment generating function. Inequalities.
- Multi-dimensional random variables (random vectors): Joint, marginal,and conditional distribution functions. Independence. Moments and moment generating function. Conditional mean and conditional variance. Discrete and absolutely continuous random variables (distributions). Multinomial and multivariate normal distributions.
- Distribution of functions of random variables including order statistics.Properties of random vectors which are equal in distribution. Exchangeable random variables and their properties.
References
- K. Rohatgi and A. K. Md. E. Saleh: An Introduction to Probabilityand Statistics, John Wiley & Sons, 2011
- Kai Lai Chung: A Course in Probability Theory (3rd Edition), AcademicPress (Elsevier)
- Robert B. Ash: Probability & Measure Theory (2nd Edition), Elsevier.(with contributions from Catherine A. Dol´eans-Dade)
- Sheldon Ross: A First Course in Probability (5th Edition), Prentice-Hall.
|
Syllabus:
|
Pre-requisite: MSO 201, None for M.Sc. 2 yr Stats
Principles of sample surveys; Simple, Stratified and unequal probability Sampling with and without replacement; ratio, product and regression method of estimation; systematic sampling; cluster and subsampling with equal unequal sizes; double sampling; sources of errors in surveys
Reference materials:
-
W.G. Cochran: Sampling Techniques, Wiley (Low price edition available)
-
Parimal Mukhopadhyay: Theory and Methods of Survey Sampling, Prentice Hall of India
-
P.V. Sukhatme, B.V Sukhatme, S. Sukhatme and C. Asok: Theory of Sample surveys with applications, IASRI, Delhi
-
P.S.R.S. Rao: Sampling Methodologies and Applications, Chapman and Hall/ CRC
-
M.N. Murthy: Sampling Theory and Methods, Statistical Publishing Society, Calcutta
-
Z. Govindrajalu: Elements of sampling theory and methods, Prentice Hall
|
|
Credits:
|
11
|
- Course No: MTH***2
- Course Title: Real Analysis
- Per Week Lectures: 3 (L),Tutorial: 1 (T),Laboratory:____(P),Additional Hours[0-2]: ________(A), Credits(3*L+2*T+P+A): 11 Duration of Course: Full Semester
- Proposing Department/IDP: Mathematics & Statistics
Other Departments/IDPs which may be interested in the proposed course:
This course is only for M.Sc. (2yr) Statistics students.
Other faculty members interested in teaching the proposed course: P. Shunmugaraj
- Proposing Instructor(s): Debasis Kundu and Neeraj Misra
- Course Description:
- Objectives: The proposed course is intended to be a basic course on real analysis for M.Sc. Statistics students.
- Contents (preferably in the form of 5 to 10 broad titles):
|
S.No.
|
Broad Title
|
Topics
|
No. of Lectures
|
|
1.
|
Basic concepts
|
Real numbers, sequences, series, tests for convergence, absolute convergence, rearrangement of terms. Open and closed sets.
|
7
|
|
2
|
Continuity and differentiability
|
Continuous functions of one real variable. Differentiation.
|
7
|
|
3
|
Integration
|
Riemann integration. Fundamental theorem of calculus. Computation of definite integrals. Improper integrals.
|
7
|
|
4
|
Convergence concepts
|
Sequences of functions, and point-wise convergence. Uniform convergence; and its relation with continuity, differentiation and integration.
|
10
|
|
5
|
Several Variable
Calculus
|
Functions of several variables. Continuity. Partial derivatives. Differentiability. Taylor’s theorem. Maxima and minima. Double integral, Fubini's theorem, Triple integration (evaluation).
|
11
|
- Pre-requisites, if any: #
- Short summary for including in the Courses of Study Booklet
Real numbers, sequences, series, tests for convergence, absolute convergence, rearrangement of terms. Open and closed sets. Continuous functions of one real variable. Differentiation. Riemann integration. Fundamental theorem of calculus. Computation of definite integrals. Improper integrals. Sequences of functions, and point-wise convergence. Uniform convergence; and its relation with continuity, differentiation and integration. Functions of several variables. Continuity. Partial derivatives. Differentiability. Taylor’s theorem. Maxima and minima. Double integral, Fubini's theorem, Triple integration (evaluation).
Recommended Books:
- R. G. Bartle andD. R. Sherbert,Introduction to Real Analysis, Wiley, 2011.
- J. E. Marsden, A. Tromba and A. Weinstein, Basic Multivariable Calculus, Springer, 1993.
- T. M. Apostol, Calculus, Vols. 1 and 2, Wiley, 1991 and 1969.
- Recommended books: Textbooks:
- R. G. Bartle andD. R. Sherbert, Introduction to Real Analysis, Wiley, 2011.
- J. E. Marsden, A. Tromba and A. Weinstein, Basic Multivariable Calculus, Springer, 1993.
Reference Books:
- T. M. Apostol, Calculus, Vols. 1 and 2, Wiley, 1991 and 1969.
- W. Rudin, Principles of Mathematical Analysis, Mac-Graw Hill, 1976.
- Any other remarks:
Dated: Proposer:____________________
Dated: DUGC Convener:________________________
The course is approved/not approved
___________________________________
Chairman,SUGC
Dated:_____________________________
- Course No: MTH***1
- Course Title: Complex Analysis
- Per Week Lectures: 3 (L),Tutorial: 1 (T),Laboratory:_____(P),Additional Hours[0-2]:________(A), Credits(3*L+2*T+P+A): 06 Duration of Course: Half Semester Module course
- Proposing Department/IDP: Mathematics & Statistics
Other Departments/IDPs which may be interested in the proposed course:
This course is only for M.Sc. (2yr) Statistics students.
Other faculty members interested in teaching the proposed course: P. Shunmugaraj
- Proposing Instructor(s): Neeraj Misra and Debasis Kundu
- Course Description:
- Objectives: The proposed course is intended to be a basic course on complex analysis for statistics masters’ students.
- Contents (preferably in the form of 5 to 10 broad titles):
|
S. No.
|
Broad Title
|
Topics
|
No. of Lectures
|
|
1.
|
Basic concepts
|
Complex Numbers, geometric representation, powers and roots of complex numbers.
|
2
|
|
2
|
Functions of complex variables
|
Functions of a complex variable. Analytic functions. CauchyRiemann equations. Elementary functions.
|
5
|
|
3
|
Integration
|
Conformal mapping (for linear transformation), Contours and contour integration. Cauchy’s theorem, Cauchy integral formula.
|
8
|
|
4
|
Power series and related topics
|
Power Series, term by term differentiation, Taylor series, Laurent series, Zeros, singularities, poles, essential singularities, Residue theorem and its Applications
|
6
|
- Pre-requisites, if any: #
- Short summary for including in the Courses of Study Booklet
Complex Numbers, geometric representation, powers and roots of complex numbers. Functions of a complex variable. Analytic functions. Cauchy-Riemann equations. Elementary functions. Conformal mapping (for linear transformation), Contours and contour integration. Cauchy’s theorem, Cauchy integral formula. Power Series, term by term differentiation, Taylor series, Laurent series, Zeros, singularities, poles, essential singularities, Residue theorem and its Applications
Recommended Books:
- J. W. Brown and R. V. Churchill, Complex Variables and Applications, McGraw-Hill, 2004.
- L. V. Ahlfors, Complex Analysis, McGraw-Hill, 1966
- Recommended books: Textbooks:
- J. W. Brown and R. V. Churchill, Complex Variables and Applications, McGraw-Hill, 2004.
Reference Books:
- L. V. Ahlfors, Complex Analysis, McGraw-Hill, 1966
- Any other remarks:
Dated: Proposer:__________________
Dated: DUGC Convener:___________________
The course is approved/not approved
Chairman,SUGC
Dated:___________________
Credits
3-0-0-0 (9)
Prerequisites
Instructor's Consent
Objectives
Curves and surfaces, Affine and projective varieties, Zariski topology, Hilbert Nullstellensatz, Bezout’s theorem, Tangent space and smoothness, irreducibility and dimension, morphisms, Grassmannian and flag varieties, determinantal varieties, Normal varieties and Zariski’s main theorem, Birartional Geometry and Resolution of singularity, Divisors and Riemann-Roch for curves
Credits
3-0-1-0 (10)
Prerequisites
MTH207A or MSO201A
Objectives
This is a fundamental course on statistical modelling - principles and methodologies of which can be extensively applied to social sciences, basic sciences, engineering sciences, medical sciences, etc., for the purpose of model building. The course not only provides a theoretical foundation to the vastly popular statistical tools used in linear regression analysis and ANOVA, but also introduces various concepts and modelling techniques to effectively analyse and model real datasets that do not conform to a set of basic underlying assumptions.
Course Contents
- Introduction to Simple and Multiple Linear Regression Models
- Estimation of the parameters using least squares and maximum likeli-hood estimation methods and their properties. [3 Lectures]
- Topics on Multivariate Normal Distribution
- Introduction to Multivariate Normal distribution, and basic properties,
- Distribution and independence of quadratic forms,
- Cochran’s theorem. [2 lectures]
- Testing of Hypotheses and Confidence Intervals
- General testing of H : Aβ = c all possible special cases.
- Goodness of fit test with introduction to R-square, etc.
- Interval estimation: Confidence band and prediction intervals, simulta-neous confidence intervals/ellipsoid, Bonferroni’s correction. [6 lectures]
- Residual Analysis and Regression Diagnostics
- Detecting outliers: Different types of residuals, Hat matrix diagonals(in connection with leverage points), Detecting and dealing with outliers.
- Departures from underlying assumptions: diagnosis and remedies. (i)Dealing with curvatures, (ii) non-constant variance and serial correlation,
(iii) Departures from normality. [6 lectures]
- Multicollinearity
- Implication of multicollinearity.
- Diagnostics: VIF and Variance Decomposition Methods.
- Remedial measures: Canonical regression and principal component regression, Ridge Regression. [4 lectures]
- Variable Selection
- Introduction to variable selection, under and over-fitting problems.
- Model selection: Adjusted R-square, Mallows Cp, , Cross-validation.
- Variable selection: Forward selection, Backward elimination, Stepwisevariable selection.
- Penalized regression: AIC, BIC criteria. [7 lectures]
- Use of Categorical Explanatory or Dummy Variables
- Indicator variables.
- Introduction to ANOVA and ANCOVA models.
- ANOVA table, splitting of sum of squares.
- Estimation and testing in the above setups. [4 lectures]
- Design preliminaries, CRD, RBD and LSD
- Introduction and Principles of designs.
- CRD- Methodology and development of analysis of variance.
- RBD- Methodology and development of analysis of variance.
- LSD- Methodology and development of analysis of variance. [6 Lec-tures]
- Generalized Linear Models
- Introduction to GLM: systematic and random components, link func-tions,
- Maximum Likelihood Estimation: iteratively re-weighted least squares,
- Applications: Logistic regression for binary data, Poisson regression forcount data. [4 Lectures]
References
- Montgomery, D. C., Peck, E. A. and Vining, G. G. (2012) Introductionto Linear Regression Analysis, Wiley Series in Probability and Statistics, Wiley, United States.
- Bapat, R. (2012). Linear Algebra and Linear Models. Springer, Germany.
- Seber G. A. F. and Lee, A. J. (2003) Linear Regression Analysis, WileySeries in Probability and Statistics, Wiley, United States.
- Draper, N. R. and Smith, H. (1998) Applied Regression Analysis, WileySeries in Probability and Statistics, Wiley, United States.
- Sengupta, D. and Jammalamadaka, S. R. (2003) Linear Models: An Integrated Approach, World Scientific, Singapore.
- Vinod, H. D. and Ullah, A. (1981) Recent Advances in Regression Methods, M. Dekker, New York, United State
Credits: 3-0-1-0 (10)
Prerequisites: MTH211A /MTH418A
Objective: The basis objective of the course is to study fundamental concepts and understand mathematical foundations of time series models and analysis. Important concepts like stationarity, auto correlation and partial auto correlation functions, standard univariate and multivariate stationary processes and their properties, statistical parameter estimation techniques and prediction, order estimation, spectral density function, spectral distribution function and periodogram analysis will be covered in the course. To have a feel and experience of handling analysis of real life time series, course project will be part of the course. At the end of the course, it is expected that a student who has done the course would know the concepts well and would also have the confidence to handle and solve real life time series data.
References:
- Introduction to Time Series and Forecasting, P.J.Brockwell & R.A.Davies, Springer, 2013.
- Time Series: Theory & Methods, P.J.Brockwell & R.A.Davies, Springer, 2019.
- Time Series Analysis, J.D. Hamilton, Princeton University Press, 2020.
- Introduction to Statistical Time Series, Wayne A. Fuller, Wiley, 1995.
Course content
Lecture Component
|
Topics
|
Lectures
|
|
Introduction and preliminary tests of time series
|
3
|
|
Mathematical formulation of time series and stationarity concepts
|
3
|
|
ACVF and ACF of stationary time series and its properties
|
2
|
|
Linear stationary processes and their time domain properties-AR, MA, ARMA
|
4
|
|
Invertibility of AR, MA, ARMA
|
3
|
|
Auto covariance generating function
|
2
|
|
Multivariate time series processes and their properties-VAR, VMA, VARMA
|
4
|
|
Random sampling from stationary time series
|
2
|
|
Parameter estimation of AR, MA and ARMA models
|
3
|
|
Best Linear predictor and Partial auto correlation function (PACF)
|
3
|
|
Model order estimation techniques
|
1
|
|
Spectral density, its properties and estimation
|
3
|
|
Spectral density function of stationary linear processes
|
3
|
|
Cross-spectrum for multivariate processes
|
2
|
|
Spectral distribution function
|
2
|
|
Periodogram analysis
|
2
|
|
Total
|
42
|
Lab Component
|
Topics
|
Lab
|
|
Handling of time series datasets
|
1
|
|
Testing for existence of trend and seasonality and estimation
|
2
|
|
Computation of ACF, PACF
|
1
|
|
Modelling of univariate and multivariate time series
|
3
|
|
Model order estimation
|
1
|
|
Residual analysis
|
1
|
|
Periodogram analysis
|
1
|
|
Term project presentations
|
4
|
|
Total
|
14
|
Credits: 3-0-1-0 (10)
Prerequisites: MTH211A/Instructor’s consent
Objective: The objective of the course is to study important statistical and AI/ML techniques used in data mining. The course would cover fundamental concepts and techniques associated with unsupervised and supervised modes of learning. Topics and concepts to be covered in the course includes: Dimension Reduction and Visualization Techniques; Chernoff faces, principal component analysis. Measures of similarity/ dissimilarity. Cluster Analysis: hierarchical and non-hierarchical techniques; Ward’s clustering. Density estimation techniques; k-nn, histogram, Kernel density estimation and parametric approaches. Association rule mining; Market Basket Analysis; apriori algorithm. Classification and Discriminant Analysis Tools; classification based on Fisher's discriminant functions, Bayes classifier, TPM and ECM minimizing classification rules, logistic discrimination rules, perceptron learning and Support Vector Machines. Tree based methods; Classification and Regression Trees. Statistical Modelling; design, estimation and inferential aspects of multiple regression, Kernel regression techniques. Neural Networks; multi-layer perceptron, feed-forward and recurrent networks, supervised ANN model building using back-propagation algorithm, ANN model for modelling and classification. Genetic algorithms, neuro-genetic models. Self-organizing Maps. At the end of the course, it is expected that a student who has done the course would know the mathematical foundation of the concepts and would also have the confidence to handle real life data.
References:
- Hastie, R. Tibshirani and J, Friedman: The elements of statistical learning: Data Mining, Inference and Prediction; Springer Series in Statistics, Springer, 2013.
- Andrew Webb: Statistical Pattern Recognition, John Wiley & Sons, 2002.
- A. Johnson and D.W. Wichern: Applied multivariate statistical analysis, Pearson, 2013.
- S. Haykin: Neural Networks: A comprehensive foundation; Prentice Hall, 1998.
Course content
Lecture Component
|
Topics
|
Lectures
|
|
Introduction and preliminary concepts
|
3
|
|
Principal component analysis
|
3
|
|
Measures of similarity/dissimilarity
|
2
|
|
Cluster Analysis
|
4
|
|
Density estimation
|
3
|
|
Association rule mining
|
3
|
|
Discriminant Analysis & Classification
|
9
|
|
Statistical Modelling
|
3
|
|
Classification & Regression Trees
|
4
|
|
Artificial Neural Networks
|
6
|
|
Genetic Algorithm
|
2
|
|
Total
|
42
|
Lab Component
|
Topics
|
Lab Hour
|
|
Multidimensional feature vector visualization
|
1
|
|
Data projection, clustering and outlier detection
|
2
|
|
Implementation of variants of apriori algorithm for ARM
|
1
|
|
Kernel density estimation
|
1
|
|
Implementation of FLDF, QDF, Logistic, SVM
|
1
|
|
Tree based classifiers and random forest
|
2
|
|
Neural network model building
|
2
|
|
Term project presentations
|
4
|
|
Total
|
14
|
Credits
0-0-0-9-9
Content
UNDER GRADUATE PROJECT I
Credits
0-0-0-9-9
Content
UNDER GRADUATE PROJECT II
Credits
0-0-0-9-9
Content
UNDER GRADUATE PROJECT III
Credits
0-0-0-9-9
Content
UNDER GRADUATE PROJECT IV
Credits
3-1-0-0 (11)
Prerequisites
MSO201A: Probability and Statistics, consent of the instructor.
Objectives
This course will present various topics involving computational tools. Focus will be on both the theory and the practical implementation of concepts.
Syllabus
Simulation of random variables from discrete, continuous, multivariate distributions and stochastic processes, Monte Carlo methods. Regression analysis, scatterplot, residual analysis. Computer intensive inference methods jack knife, bootstrap, cross validation, Monte Carlo methods and permutation tests. Graphical representation of multivariate data, Cluster analysis, Principal component analysis for dimension reduction.
References
- Sheldon M. Ross: Simulation, Academic Press, Fourth Edition, 2006.
- Efron and R. J. Tibshirani: An Introduction to the Bootstrap, Chapman and Hall, 1994.
- S. Everitt, S. Landau, M. Leese, D. Stahl: Cluster Analysis, Wiley,2011.
- Trevor Hastie, Robert Tibshirani, Jerome Friedman, Springer, 2001.
- R. Gilks, S. Richardson, D. J. Spiegelhalter: Markov Chain Monte Carlo in Practice, Chapman and Hall
Credits
3-1-0-0 (11)
Prerequisites
MSO 201 / Instructor’s consent
Course Contents
- Analysis of completely randomized design, randomized block design, Latinsquares design;
- Split plot, 2 and 3-factorial designs with total and partial confounding,two way non-orthogonal experiment, BIBD, PBIBD;
- Analysis of covariance, missing plot techniques;
- First and second order response surface designs.
References
- Scheffe: The Analysis of Variance, Wiley, 1961.
- Toutenburg & Shalabh: Statistical Analysis of Designed Experiments,Springer, 2009.
- C. Montagomery: Design & Analysis of Experiments, 5th Edition,Wiley, 2001
- D. Joshi: Linear Estimation and Design of Experiments, Wiley Eastern,1987.
- George Casella: Statistical Design, Springer, 2008.
- Max D. Morris: Design of Experiments- An Introduction Based on LinearModels, CRC Press, 2011.
- Giri: Analysis of Variance, South Asian Publishers, New Delhi, 1986.
- Sahai and M.I. Ageel: The Analysis of Variance-Fixed, Random andMixed Models, Springer, 2001.
- Aloke Dey: Incomplete Block Design, Hindustan Book Agency 2010.
Credits
3-1-0-0 (11)
Prerequisites
MTH418A
Objectives
The objective of the course is to impart necessary knowledge about theoretical foundations of multivariate distribution theory, with special emphasis on Multivariate Gaussian distribution, statistical inferential aspects related to random sampling from multivariate populations and to learn various important applied multivariate data analysis tools and techniques, with a view to understand the mathematical derivation and justification of these methods and further to implement them for solving real life problems.
Course Contents
- Multivariate normal distribution, assessing normality, (9 lectures)
- Wishart and Hotelling’s T2, (9 lectures)
- Comparisons of several multivariate means, MANOVA; (3 lectures)
- Principal Component Analysis, (3 lectures)
- Factor Analysis; (3 lectures)
- Canonical Correlations; (4 lectures)
- Discrimination & Classification; (6 lectures)
- Cluster Analysis. (3 lectures)
References
- Mardia, K. V., Bibby, J. M., Kent, J. T. (1979). Multivariate Analysis.United Kingdom: Academic Press.
- Johnson, R. A., Wichern, D. W. (2019). Applied Multivariate StatisticalAnalysis. United Kingdom: Pearson.
- Muirhead, R. J. (2009). Aspects of Multivariate Statistical Theory. Germany: Wiley.
- Anderson, T. W. (2003). An Introduction to Multivariate Statistical Analysis. United Kingdom: Wiley.
- Hastie, T., Friedman, J., Tibshirani, R. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Germany: Springer New York.
- Brenner, D., Bilodeau, M. (1999). Theory of Multivariate Statistics. Germany: Springer.
- Johnson, R. A., Wichern, D. W. (2019). Applied Multivariate Statistical Analysis. United Kingdom: Pearson
|
Syllabus:
|
Pre-requisite: MTH 418 / Instructor's consent
Group families; Principle of invariance and equivariant estimators- location family, scale family, location-scale family; General Principle of equivariance; Minimum risk equivariant estimators under location scale and location-scale families; Bayesian estimation; prior distributions; posterior distribution; Bayes estimators; limit of Bayes estimators; hierarchical Bayes estimators; Generalized Bayes estimators; highest posterior density credible regions; Minimax estimators and their relationships with Bayes estimators; admissibility; Invariance in hypothesis testing; Review of convergence in probability and convergence in distributions; consistent estimators; Consistent and Asymptotic Normal (CAN) estimators; BAN estimator; asymptotic relative efficiency (ARE); Limiting risk efficiency (LRE); Limiting risk deficiency (LRD; CRLB and asymptotically efficient estimator; large sample properties of MLE.
Reference materials:
-
E. L. Lehmann and G. Casella : Theory of Point Estimation, Springer.
-
J. O. Berger: Statistical Decision Theory and Bayesian Analysis, Springer.
-
E. L. Lehmann and J. P. Romano: Testing Statistical Hypotheses, Springer.
-
G. Casella and R. L. Berger: Statistical Inference, Thomson Learning.
-
Jun Shao: Mathematical Statistics, Springer.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 418 / Instructor's consent
Order statistics, Run tests, Goodness of fit tests, rank order statistics, sign test and signed rank test. General two sample problems, Mann Whitney test, Linear rank tests for location and scale problem, k-sample problem, Measures of association, Power and asymptotic relative efficiency, Concepts of jack knifing, Bootstrap methods.
Reference materials:
-
Larry Wasserman: All of Nonparametric Statistics, Springer Texts in Statistics, 2006.
-
J. D. Gibbons and Subhabrata Chakraborti: Nonparametric Statistical Inference, CRC Press, 2010.
-
R. H. Randles and D. A. Wolfe: Introduction to the Theory of Nonparametric Statistics, Krieger Pub Co., 1991.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MSO 201/ Instructor's consent
Fundamental components of time series; Preliminary tests of a time series-test for randomness, test for trend, test for seasonality; Estimation/elimination of trend and seasonality- moving average smoothing, least squares method, method of differencing; Mathematical formulation of time series; Stationarity concepts- strict stationary, stationary up to order m, covariance stationary; stationarity of complex valued time series; Auto Covariance and Auto correlation functions of stationary time series and its properties; Linear stationary processes and their time domain properties- AR, MA, ARMA, seasonal, non-seasonal and mixed models; ARIMA models; Invertibility of linear stationary processes; Auto covariance generating function; Multivariate time series processes and their properties-VAR, VMA and VARMA; and ARIMA; Random sampling from stationary time series-estimators of mean and ACF and their small sample and asymptotic properties; Parameter estimation of AR, MA and ARMA models-LS approach, estimation based on Yule-Walker for AR and ML approach for AR, MA and ARMA models, Asymptotic distribution of MLE; Best Linear predictor and Partial auto correlation function (PACF); Model identification with ACF and PACF; Model order estimation techniques-AIC, AICC, BIC, EDC, FPE; Frequency domain analysis- spectral density and its properties, spectral density function of stationary linear processes, cross-spectrum for multivariate processes, Spectral distribution function, estimation spectral density function; Periodogram analysis.
Reference material(s):
-
P. J. Brockwell and R.A. Davis: Time Series: Theory and Methods, Springer.
-
P. J. Brockwell and R.A. Davis: Introduction to Time Series and Forecasting, Springer.
-
J. D. Hamilton: Time Series Analysis, Princeton University Press.
-
T. W. Anderson: The Statistical Analysis of Time Series.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 102 / Instructor's consent
Computer arithmetic. Vector and matrix norms. Condition number of a matrix and its applications. Singular value decomposition of a matrix and its applications. Linear least squares problem. Householder matrices and their applications. Numerical methods for matrix eigenvalue problem. Numerical methods for systems and control.
Reference materials:
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 102 / Instructor's consent
Introduction and motivation, Weak formulation of BVP and Galerkin approximation, Piecewise polynomial spaces and finite element method, Computer implementation of FEM, Results from Sobolev spaces, Variational formulation of elliptic BVP, Lax-Milgram theorem, Estimation for general FE approximation, Construction of FE spaces, Polynomial approximation theory in Sobolev spaces, Variational problems for second order elliptic operators and approximations. Mixed methods, Iterative Techniques.
Reference materials:
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 102 / Instructor's consent
Review and General Properties of Navier Stokes Equations; Some Exact solutions of NS equations; Introduction to boundary layer theory; Introduction to turbulent flow; Introduction to compressible flow; Applications.
Reference materials:
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: MTH 102 / Instructor's consent
Preliminaries: Introduction to algorithms; Analysing algorithms: space and time complexity; growth of functions; summations; recurrences; sets, etc. Greedy Algorithms: General characteristics; Graphs: minimum spanning tree; The knapsack problem; scheduling. Divide and Conquer: Binary search; Sorting: sorting by merging, quicksort. Dynamic Programming: Elements of dynamic programming; The principle of optimality; The knapsack problem; Shortest paths; Chained matrix multiplication. Graph Algorithms: Depth first search; Breadth first search; Backtracking; Branch and bound. Polynomials and FFT: Representation of polynomials; The DFT and FFT; Efficient FFT implementation. Number Theoretic Algorithms: Greatest common divisor; Modular arithmetic; Solving modular linear equations. Introduction to cryptography. Computational Geometry: Line segment properties; Intersection of any pair of segments; Finding the convex hull; Finding the closest pair of points. Heuristic and Approximate Algorithms: Heuristic algorithms; Approximate algorithms; NP hard approximation problems
Reference materials:
|
|
Credits:
|
11
|
Units
3-0-0-0 [9]
Prerequisites
MTH204 (Abstract Algebra), MSO202A (Complex Analysis)
Course Description
A positive integer is called a congruent number if it is the area of a rational right angled triangle. Fibonacci showed that 5,6,7 are congruent numbers and Fermat proved that 1 is not a congruent number. Indeed, the problem of classifying congruent numbers can be traced back to at least 10th century and is still unresolved. In particular, the following conjecture is open: Given a positive integer n, is there a (finite step) algorithm to determine if n is a congruent number or not? Modern developments relate the congruent number problem to the arithmetic of elliptic curves and modular forms. In this course, we will study the basic theory of elliptic curves, modular forms and their relation with the congruent number problem. Note that the theory of elliptic curves have significant applications in cryptography.
Course content and lecture plan:
- Congruent numbers: definition, example, history, basic results and relation with elliptic curves [4 lectures]
- Some basics of projective geometry and algebraic curves. [3 lectures]
- Elliptic curves over complex numbers. [3 lectures]
- Elliptic curve in Weierstrass form, group law of elliptic curves. [4 lectures]
- Elliptic curves over finite fields. [3 lectures]
- Congruent elliptic curve, points of finite order. [2 lectures]
- Hasse-Weil L-function of an elliptic curve, functional equation for the Lfunction of a congruent elliptic curve. [3 lectures]
- Modular forms: action of on upper half plane, fundamental domain, modular forms for and congruence subgroups. [4 lectures]
- Eisenstein series, cuspforms, Ramanujan ∆-function. [2 lectures]
- Hecke operators, eigenforms, L-function of a modular form. [3 lectures] 1/2 integral weight modular forms, definition and examples, Θ-function. [4 lectures]
- Statement of Coates-Wiles theorem, Shimura’s correspondence. [2 lectures]
- Tunnel’s criterion for congruent number. [2 lectures]
- Heegner points. [3 lectures]
References
- Introduction to elliptic curves and modular forms, N. Koblitz, GTM 97,Springer-Verlag.
- Rational points on elliptic curves, J. H. Silverman and J. Tate, UTM, SpringerVerlag.
- The arithmetic of elliptic curves, J. H. Silverman, GTM 106. SpringerVerlag.
- A course in Arithmetic, J. P. Serre, GTM 07, Springer-Verlag.
- A first course in Modular forms, F. Diamond and J. Shurman, GTM 228, Springer-Verlag.
- A classical Diophantine problem and modular forms of weight 3/2, J. B.Tunnel, Math. 72, 307-352, 1983.
- Congruent number problem , Ye Tian, ICCM Not. 5 no. 1, 51-61, 2017.
|
Syllabus:
|
Pre-requisite: MSO201 / Instructor's consent
Introduction to Data Mining; supervised and un-supervised data mining, virtuous cycle. Dimension Reduction and Visualization Techniques; Chernoff faces, principal component analysis. Feature extraction; multidimensional scaling. Measures of similarity/ dissimilarity. Cluster Analysis: hierarchical and non-hierarchical techniques. Classification and Discriminant Analysis Tools; classification based on Fisher's discriminant functions, Bayes classifier, TPM and ECM minimizing classification rules, logistic discrimination rules, perceptron learning and Support Vector Machines. Density estimation techniques; parametric and Kernel density estimation approaches. Statistical Modelling; design, estimation and inferential aspects of multiple regression, Kernel regression techniques. Tree based methods; Classification and Regression Trees. Neural Networks; multi-layer perceptron, feed-forward and recurrent networks, supervised ANN model building using back-propagation algorithm, ANN model for classification. Genetic algorithms, neuro-genetic models. Self-organizing Maps.
Reference materials:
-
T. Hastie, R. Tibshirani and J, Friedman: The elements of statistical learning: Data Mining, Inference and Prediction; Springer Series in Statistics, Springer, 2013.
-
R. A. Johnson and D.W. Wichern: Applied multivariate statistical analysis, Pearson, 2013.
-
A. R. Webb: Statistical Pattern Recognition, John Wiley & Sons, 2002.
-
S. S. Haykin: Neural Networks: A comprehensive foundation; Prentice Hall, 1998.
-
D. J. Hand, H. Mannila and P. Smith: Principles of Data Mining, MIT Press, Cambridge, 2001.
|
|
Credits:
|
11
|
|
Syllabus:
|
Pre-requisite: None (Only for M.Sc students)
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: None (Only for M.Sc students)
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 428 / Instructor's consent
Elementary mathematical models; Role of mathematics in problem solving; Concepts of mathematical modelling; System approach; formulation, Analyses of models; Sensitivity analysis, Simulation approach; Pitfalls in modelling, Illustrations
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 428 / Instructor's consent
Biofluid dynamics; Blood flow & arterial diseases; Transport in intestines& lungs; Diffusion processes in human systems; Mathematical study of nonlinear Volterra equations, Stochastic & deterministic models in population dynamics and epidemics.
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH204 / Instructor's consent
Fields: Definition and examples, Irreducibility Criterions, Prime Subfield, Algebraic and transcendental elements and extensions, Splitting field of a polynomial. Existence and uniqueness of algebraic closure. Finite fields, Normal and separable extensions, Inseparable and purely inseparable extensions. Simple extensions and the theorem of primitive elements, Perfect fields.Galois Extension and Galois groups. Fundamental theorem of Galois Theory. Applications of Galois Theory: Roots of unity and cyclotomic polynomials, Wedderburn's and Dirichlet's theorem. Cyclic and abelian extensions, Fundamental Theorem of Algebra, Polynomials solvable by radicals, Symmetric functions, Ruler and compass constructions. Traces and norms, Hilbert's theorem-90, Dedekind's theorem of Linear Independence of Characters. Inverse Galois Problem.(Time permitting: Simple transcendental extension and Luroth's theorem. Infinite Galois Extension and Krull's theorem.)
Reference materials:
-
S. Lang: Algebra.
-
M. Artin: Algebra.
-
D. S. Dummit and R.M. Foote: Abstract Algebra.
-
Patrick Morandi: Field and Galois Theory, GTM 167, Springer-Verlag.
-
M. P. Murthy, K. G. Ramanathan, C. S. Seshadri, U. Shukla and R. Sridharan: Galois Theory, http://www.math.tifr.res.in/~publ/pamphlets/galoistheory.pdf
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH204 / Instructor's consent
Review of basic notions of Rings and Modules, Noetherian and Artinian Modules, Exactness of Hom and tensor, Localization of rings and modules, Primary decomposition theorem, Integral extensions, Noether normalization and Hilbert Nullstellensatz, Going up and Going down theorem, Discrete Valuation rings and Dedekind domains, Invertible modules, Modules over Dedekind domain, Krull dimension of a ring, Hilbert polynomial and dimension theory for Noetherian local ring, Height of a prime ideal, Krull's principal ideal theorem and height theorem. Completions.
Reference materials:
-
M. Atiyah and I. Macdonald: An introduction to commutative algebra.
-
N. S. Gopalakrishnan: Commutative Algebra, Oxonian Press. 1984.
-
D. Eisenbud: Commutative algebra with a view toward algebraic geometry.
-
H. Matsumura: Commutative algebra.
-
I. Kaplansky: Commutative rings, Allyn and Becon, 1970.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH204 / Instructor's consent
Review of Basic Ring theory: Integral domain and field of Fraction, Prime Avoidance theorem, Unique factorization domain, Principal Ideal domain, Euclidean domain, Gauss lemma, Polynomial Rings, Power series ring, Group ring, Modules: Vector spaces, Definition and examples of modules, Free modules, submodules and quotient modules, isomorphism theorems, Direct sum and direct products, Nakayama lemma, Finitely generated modules over a PID and applications, Rational Canonical form, Smith normal form, Jordan Canonical form, Jordan-Holder series, Projective and Injective Modules, Semi-simple rings and Modules, The Artin-Wedderburn theorem, Noetherian rings and Modules, Artinian rings and Modules, Hilbert basis theorem. (Time permitting: Artinian local rings and structure theorem of Artinian rings, Tensor products and multilinear forms, Exterior and Symmetric Algebra, Direct and Inverse system of modules.)
Reference materials:
-
D.S. Dummit and R.M. Foote: Abstract Algebra.
-
N. S. Gopalakrishnan: Commutative Algebra, Oxonian Press. 1984.
-
S. Lang: Algebra, GTM 211, Springer-Verlag.
-
C. Musili: Introduction to Rings and Modules, Narosa Publication.
-
T. W. Hungerford: Algebra, GTM, Springer.
-
N. Jacobson: Basic Algebra I, Basic Algebra II, Dover Publications.
-
M. Atiyah and I. Macdonald: An introduction to commutative algebra.
|
|
Credits:
|
9
|
Credits
3-0-0-0 [9]
Prerequisites
MTH309 Probability Theory or MTH754 Probability Theory
Syllabus
- Preliminaries: σ-fields, random variables, Expectation, Lp spaces with respect to Probability measures (4 Lectures)
- Conditional Probability and Conditional Expectation (2 Lectures)
- Brownian motion: Definition, Construction/Proof of existence, path properties and Martingale property (12 Lectures)
- Stochastic/Itˆo Integration: Construction, Itˆo isometry, properties of Itˆointegral, Girsanov’s Theorem. (If time permits) Martingale Representation Theorem (12 Lectures)
- Stochastic Differential Equation: various notions of solutions, existenceand uniqueness results (8 Lectures)
- Application to Mathematical Finance: Black-Scholes formula (4 Lectures)
References
- Bernt Oksendal, Stochastic Differential Equations - an introduction with applications, sixth edition. Universitext, Springer-Verlag, 2003.
- Ioannis Karatzas & Steven E. Shreve, Brownian Motion and Stochastic Calculus, 2nd Edition. Graduate Texts in Mathematics 113, SpringerVerlag, 1991.
- Philip E. Protter, Stochastic Integration and Differential Equations, second edition. Stochastic Modelling and Applied Probability. SpringerVerlag, 2004.
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
General theory of two dimensional manifolds, orientable surfaces, homology and cohomology of surfaces, Riemann surfaces, line bundles and vector bundles, Riemann-Roch theorem, Riemann bilinear relations, AbelJacobi map, Torelli’s-theorem and Theta divisors.
|
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
The course content is divided into three parts. While the First part focuses on the approximation of functions, the other two deal with material related to the solution of linear and non-linear operator equations. The course will broadly cover the following topics:
I. Theory of Approximations: Metric Spaces, Linear Spaces, Normed and Banach Spaces, Inner product and Hilbert Spaces; Problems on the Best Approximation, Orthogonal Expansions and Fourier Series in a Hilbert Space; Chebyshev Polynomials and their properties, Some Extremal Polynomials
II. Linear Operators and Functionals: Linear Operators in Banach Spaces, Spaces of Linear Operators, Inverse Operators, Linear Operator Equations, Condition Measure of Operator; Spectrum and Spectral Radius of Operator, Convergence Conditions for the Neumann Series, Perturbations Theorem; Representation of Functions by Integrals; Linear Functionals and Adjoint Space, Adjoint, Selfadjoint, Symmetric Operators; Eigenvalues and Eigenelements of Selfadjoint and Symmetric Operators; Quadrature Functionals and Generalized Solutions of Operator Equations; Variational Methods, Variational Equations; Compact Operators; Sobolev Spaces, Generalized Solution of the Dirichlet Problem for Elliptic Equations of the Second Order
III. Iteration methods for the solution of operator equations: General Theory of Iteration Methods; Chebyshev Iteration Methods, Descent Methods, Newton Method; Succesive Approximation Method for Inverse Operator; Stability and Optimization of Explicit Difference Schemes for Stiff Differential Equations
|
|
Course Contents:
|
Pre-requisite: Instructor's Consent (knowledge of complex analysis and functional analysis, is desirable)
This course mainly gives an introduction to Hardy spaces and composition operators on them. The course will broadly cover the following topics:
|
Topics
|
No. of Lectures
|
|
Analytic functions – Möbius transformations – Fixed points – Classification of
Möbius transformations – Self-maps of the unit disk – Hilbert spaces – Bounded operators – Adjoint of an operator – Functional Hilbert spaces – Reproducing kernels.
|
7
|
|
Hardy space H2 – Growth estimate – Consequences – Hp spaces – Zeros – Blaschke
products – Inner functions – Mean convergence theorem – Multiplication operators – Beurling’s theorem – Invariant subspace problem – Equivalent conjecture.
|
8
|
|
Composition operators – Introduction and motivation – Automorphic composition
operators – Littlewood’s theorem – Norm estimates.
|
5
|
|
Compact composition operators – Various compactness theorems – Compactness and
Weak convergence – Compactness and Univalence.
|
10
|
|
Angular derivatives and Iteration – Denjoy-Wolff theorem – König’s theorem for eigen values – General compactness theorem.
|
8
|
|
Introduction to various function spaces such as Bergman space, Dirichlet space and Bloch space and natural operators on them. Open problems.
|
2
|
|
Total lectures:
|
40
|
Recommended books:
-
Joel H. Shapiro, Composition Operators and Classical Function Theory, Springer, New York, 1993.
-
Peter L. Duren, Theory of Hp Spaces, Academic. Press, New York and London, 1970.
-
Carl C. Cowen and Barbara I. MacCluer, Composition Operators on Spaces of Analytic Functions, CRC Press, Florida, 1995.
|
|
Credits:
|
L-T-P-A [C] -- 3-0-0-0 [9]
|
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Complex manifolds, Almost complex structures; Exterior forms on complex manifolds, Kähler metrics. ; Hodge theory for Kähler manifolds; Holomorphic vector bundles; Line bundles and divisors; Cohomology of holomorphic vector bundles; Vanishing Theorems and the Kodaira Embedding Theorem; Curvature of Kähler manifold; The Calabi Conjecture.; Riemann holonomy groups, The Kähler holonomy groups; Introduction to moduli spaces; Deformation theory for compact complex manifolds.
|
|
Syllabus:
|
Pre-requisite: MTH301 / Instructor's consent
Algebra, σ-algebra, measure, measurable functions, simple functions, integration, Fatou's lemma, monotone convergence theorem, Dominated convergence theorem, Riesz representation theorem, regular Borel measure, Lebesgue measure, 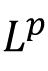 spaces, completeness of spaces, completeness of 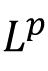 and denseness results in and denseness results in 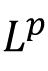 , signed and complex measures, Radon-Nikodym theorem, Lebesgue decomposition theorem, dual of , signed and complex measures, Radon-Nikodym theorem, Lebesgue decomposition theorem, dual of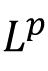 spaces, dual of spaces, dual of 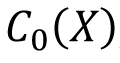 , product measures, Fubini's theorem and its application, differentiation of measures. , product measures, Fubini's theorem and its application, differentiation of measures.
Reference materials:
-
P. R. Halmos: Measure Theory. D. Van Nostrand Company, Inc., New York, 1950.
-
Walter Rudin: Real and complex analysis, McGraw-Hill international editions.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH301 / Instructor's consent
Fourier transform on , , 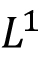 and and 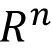 theory, Complex interpolation, theory, Complex interpolation, 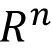 theory, Paley-Wiener theorem, Wiener-Tauberian theorem, Hilbert transform, Maximal function, real interpolation,Riesz transform, transference principle, Multipliers and Fourier Stieljes transform, Calderon-Zygmund singular integrals, Littlewood-Paley theory. theory, Paley-Wiener theorem, Wiener-Tauberian theorem, Hilbert transform, Maximal function, real interpolation,Riesz transform, transference principle, Multipliers and Fourier Stieljes transform, Calderon-Zygmund singular integrals, Littlewood-Paley theory.
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 301 / Instructor's consent
Differentiable manifolds; Tangent space. Vector fields; Frobenius theorem; Relation between Lie sub-algebras & Lie subgroups; Cartans theorem on closed subgroups; One parameter subgroups; Exponential maps; Adjoint representation; Homogeneous spaces; Compact Lie groups; Symmetric spaces
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 301 / Instructor's consent
Fourier Analysis: A review, Convolutions, Multipliers and Filters, Poisson Summation Formula, Shannon Sampling Discrete Fourier Transform, Fast Fourier Transform, Discrete Wavelets, Continuous Wavelets, Uncertainty Principles, Radar Ambiguity, Phase Retrieval, Random Transform, Basic Properties, Convolution and Inversion, Computerized Tomography
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 304 / Instructor's consent
Classification of 2dimensional surfaces; Fundamental group; Knots and covering spaces; Braids and links; Simplicial homology groups and applications; Degree and Lefschetz Number, Borsuk Ulam Theorem, Lefschetz Fixed Point Theorem
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 301 / Instructor's consent
Best approximation in normed spaces, Tchebycheff systems, Tchebycheff Weierstrass Jackson Bernstein Zygmund Nikolaev etc. theorems, Fourier series, Splines, Convolutions, Linear positive, Variation diminishing, Simultaneous etc. approximations. Direct inverse saturation theorems, Applications.
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 301 / Instructor's consent
Unbounded Operators, Matrix representation, Self-adjointness Criterion, Quadratic Forms, Differential Operators, Self-adjoint Extensions, Functional Calculus, Spectra of Self-adjoint Operators, Semi analytic vectors, Theorems of Nelson and Nussbaum, States and Observables, Super selection Rules, Position and Momentum, An Uncertainty Principle of Bargmann, Canonical Commutation Relations, Schrodinger representations, Schrodinger Operators, Self-adjointness, A Theorem of Kato, Spectral Theory for Schrodinger Operators, Discrete Spectrum, Essential Spectrum
Reference materials:
-
N. Akhiezer and I. Glazman: Theory of Linear Operators in Hilbert Space II, Dover, 1961.
-
J. Blank, P. Exner and M. Havlivcek: Hilbert Space Operators in Quantum Physics, Springer, 2008.
-
T. Kato: Perturbation Theory, Springer, 1976.
-
M. Miklavcic: Applied Functional Analysis and Partial Differential Equations, World Scientific, 1998.
-
M. Reed and B. Simon: Methods of Modern Mathematical Physics II, Academic Press, 197
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 301 / Instructor's consent
Models of Hyperbolic Space: Upper Half Space Model & Disc Model; Isometries of Hyperbolic Space; Geodesics; Slimness of Triangles and Exponential Divergence of Geodesics in Hyperbolic Space; Isoperimetric Inequalities in Euclidean & Hyperbolic Space; Boundary of Hyperbolic Space; Review of Covering Spaces, Local Isometries and Fundamental groups; Properly Discontinuous Group actions; Fundamental Domains; Hyperbolic Surfaces
Reference materials:
-
R. Benedetti and C. Petronio: Lectures on Hyperbolic Geometry; Springer Verlag.
-
B. Maskit: Kleinian Groups, Springer Verlag.
-
M. R. Bridson and A Haefliger: Metric Spaces of Non-Positive Curvature, Springer.
-
Svetlana Katok: Fuchsian Groups, The University of Chicago Press.
-
B. H. Bowditch: A course on geometric group theory, preprint.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 301 / Instructor's consent
Preliminaries, Elements of basis theory, Types of bases, Summability (summation of infinite series), Koethe sequence spaces, Bases in OTVS, Isomorphism theorems
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite(s): MTH 404, MTH 405
Introduction to Banach algebras: Gelfand Transform, commutative Banach algebras, Gelfand-Naimark Theorem, Spectral Theorem for normal operators and its applications to operators on a Hilbert space. The theory of Fredholm operators: spectral theory of compact operators (Fredholm Alternative). Operator matrices: Invariant and Reducing subspaces, the theory of ideals of compact operators (if time permits).
(Please note that some topics mentioned here are tentative and subject to change depending on the instructor. There is a flexibility of adding/deleting some topics.)
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH301 / Instructor's consent
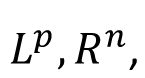 , Riesz Interpolation Theorem, Hilbert Transform, Hardy-Littlewood Maximal function, , Riesz Interpolation Theorem, Hilbert Transform, Hardy-Littlewood Maximal function, 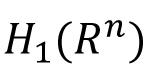 and BMO, Distributions, Important example of distributions, Calderon-Zygmund Distributions. and BMO, Distributions, Important example of distributions, Calderon-Zygmund Distributions.
Reference materials:
-
E. M. Stein and R. Shakarchi: Functional Anlaysis, Princeton Lect. In AnalysisVol-4, 2011
-
W. Rudin: Functional Analysis, Tata-McGraw Hill
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH301 / Instructor's consent
Banach Algebras and Spectral theory, Locally compact groups, Basic representation theory, Analysis on Locally compact abelian group, Analysis on compact groups, Group 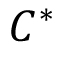 -algebra and structure of dual space. -algebra and structure of dual space.
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 301 / Instructor's consent
Topological linear spaces, Equicontinuity, Function spaces, Convexity & convex topological spaces, Hahn Banach theorem, Barrelled spaces, Principle of uniform boundedness, Bornological spaces, Duality theory (Mackey Arens Theorem, Mackey Topology, S-topology, Polarity)
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH301 / Instructor's consent
Geometry of 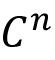 : Reinhardt Domains: Definition and Examples, Absolute spaces. Elementary Theory of SCV: Holomorphic Functions: Definition and Examples, C-R Equations and its Applications. Power Series: Definition and Examples, Abel's Lemma and its Consequences, Complete Reinhardt Domains: Definition and Examples, Cauchy's Integral Formula for Poly-discs and its Consequences. Some New Phenomena in SCV: Biholomorphic Inequivalence of Unit Polydisc and Unit Ball, Zeroes of holomorphic functions are never isolated, Logarithmically Convex and Complete Domains: Definition and Examples, Hartogs' Phenomenon: Continuation on Reinhardt Domains. Singularities of Holomorphic Functions: Analytic Sets: Definition and Examples, Riemann Removable Singularity Theorems and its Applications, Hartogs' Kugelsatz, Zero Set of a Holomorphic Function: Topological Properties. Local Properties of Holomorphic Functions: Weierstrass Preparation Theorem, Weierstrass Division Theorem, Ring of Germs of Holomorphic Functions is Noetherian and an UFD, Local Parametrization for the Zero Set of a Holomorphic Function. Domains of Holomorphy: Domains of Holomorphy: Definition and Examples, Various Notions of Convexity: Definition and Examples, Logarithmically Convex Complete Domains as Domain of Convergence, Theorem of Cartan and Thullen. : Reinhardt Domains: Definition and Examples, Absolute spaces. Elementary Theory of SCV: Holomorphic Functions: Definition and Examples, C-R Equations and its Applications. Power Series: Definition and Examples, Abel's Lemma and its Consequences, Complete Reinhardt Domains: Definition and Examples, Cauchy's Integral Formula for Poly-discs and its Consequences. Some New Phenomena in SCV: Biholomorphic Inequivalence of Unit Polydisc and Unit Ball, Zeroes of holomorphic functions are never isolated, Logarithmically Convex and Complete Domains: Definition and Examples, Hartogs' Phenomenon: Continuation on Reinhardt Domains. Singularities of Holomorphic Functions: Analytic Sets: Definition and Examples, Riemann Removable Singularity Theorems and its Applications, Hartogs' Kugelsatz, Zero Set of a Holomorphic Function: Topological Properties. Local Properties of Holomorphic Functions: Weierstrass Preparation Theorem, Weierstrass Division Theorem, Ring of Germs of Holomorphic Functions is Noetherian and an UFD, Local Parametrization for the Zero Set of a Holomorphic Function. Domains of Holomorphy: Domains of Holomorphy: Definition and Examples, Various Notions of Convexity: Definition and Examples, Logarithmically Convex Complete Domains as Domain of Convergence, Theorem of Cartan and Thullen.
Reference materials
-
V. Scheidemann: Introduction to Complex Analysis in Several Variables, Birkhauser Verlag, Basel, 2005.
-
R. Range: Holomorphic Functions and Integral Representations in Several Complex Variables,
Springer-Verlag, New York, 1986.
-
R. Narasimhan: Several Complex Variables, Univ. of Chicago Press, Chicago, 1995.
-
L. Hormander: Introduction to Complex Analysis in Several Variables, North-Holland Publishing Co. Amsterdam, 1990.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH201, MTH204
Definitions and first examples. Classical Lie algebras. Ideals and homomorphisms. Nilpotent Lie algebras. Engel's theorem. Solvable Lie algebras. Lie's theorem. Jordan Chevalley Decomposition. Radical and semisimplicity. The Killing form and Cartan's criterion. The structure of semisimple Lie algebras. Complete reducibility and Weyls theorem. Representation theory of the Lie algebra sl(2). Total subalgebras and root systems. Integrality properties. Simple Lie algebras and irreducible root systems.
Reference materials:
-
J. E. Humphreys: Introduction to Lie Algebras and Representation Theory, Berlin, New York, 1972.
-
J. P. Serre: Complex semi-simple Lie algebras (translated from French: Algebras de Lie complex semi-simple).
-
N. Jacobson: Lie algebras, Dover publication.
|
|
Credits:
|
9
|
Credits
3-0-0-0(9)
Prerequisites
Prerequisites: Instructor’s consent.
Aims of the course
Model theory can be roughly described as “logic + algebra” and it studies classes of mathematical structures from the logical perspective. Many branches of mathematics are titled ‘- theory’ where - is a placeholder for group, field, order etc. where a theory is a set of axioms/sentences written in a formal language, and a ‘model’ of such a theory is a structure that satisfies all the axioms. The course aims to cover some general abstract techniques and then focus on some interesting theories/results across different parts of mathematics including algebra, lattices and algebraic geometry.
Syllabus
- The place of model theory in pure mathematics.
- Structures and homomorphisms: syntax, structures, homomorphism, isomorphism, substructure, embedding, examples.
- Semantics: evaluation of terms, satisfaction of formulas, elementary embedding, theory, elementary equivalence, examples.
- Compactness: Ultrafilters, product structures, ultraproducts, compactness theorem, applications, Lowenheim-Skolem theorem.
- Theories: dense linear orders (DLO), algebraically closed fields (ACF),real closed fields (RCF).
- Categoricity: definition, Vaught’s test, back-and-forth method, Ryll-Nardzewskitheorem, Morely’s categoricity theorem.
- Quantifier elimination: explanation and characterization, Chevalley’s theorem, Tarski-Seidenberg theorem.
- Types: definition, complete types, Stone spaces, omitting types theorem.
- Grothendieck ring: definable bijections, Grothendieck group of a monoid,Grothendieck ring of a structure, examples.
- Miscellaneous topics: Fraisse limits, imaginaries, geometries, model-completeness.
References
- Chang, Chen Chung, and H. Jerome Keisler. Model theory. Vol. 73. Elsevier, 1990.
- Hodges, Wilfrid. A shorter model theory. Cambridge university press, 1997.
- Hodges, Wilfrid. Model theory. Vol. 42. Cambridge University Press, 19.
- Marker, David. Model theory: an introduction. Vol. 217. Springer Science & Business Media, 2006.
|
Credits:
|
3-1-0-0 (11)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Examples of different types of spatial data and possible scientific questions: point-referenced data, areal data, pointpattern data; Review of multivariate statistical inference, Gaussian processes, Review of linear models, Review of matrix algebra; Spatial covariance and variogram, Estimation of variogram, Variogram model fitting, Spectral representation; Spatial regression and ordinary kriging, Robust kriging, Universal kriging, Simulation of spatial processes, R packages for data visualization and geostatistical modeling and applications of geostatistics; Some examples of areal datasets, conditional autoregressive models, simultaneous autoregressive models, Markov random fields; Gaussian maximum likelihood estimation and properties of the estimators; Point pattern data examples, Point referenced spatial data modeling: Inhomogeneous Poisson process, Cox process, Markov point process, Marked-Markov point process; Multivariate spatial and spatiotemporal modeling, Hierarchical spatial models for continuous and discrete responses, Remote sensing data analysis, Bayesian spatial models, Copula-based models, Large spatial data modeling, Nonstationary spatial modeling
|
|
Syllabus:
|
Pre-requisite: MTH301, MTH 403 / Instructor's consent
Subharmonic Functions: Subharmonic Functions: Definition and Examples, Maximum Principles, Montel's Theorem for Harmonic Functions, Harnack's Inequality, Montel's Theorem for Positive Harmonic Functions. Dirichlet Problem: Dirichlet Problem for Bounded Domains, Dirichlet Problem for Disc and Punctured Disc, Peron Method, Harmonicity of the Peron Solution, Sub harmonic Barrier, Riemann Mapping Theorem, Uniformization Theorem for Riemann Sphere. Green's Functions: Green's Formulae, Green's Function for Unit Disc and Complex Plane, Harmonic Measure, Green's unction for Domains with Analytic Boundary, Green's Function for General Domains. Riemann Surfaces: Abstract Riemann Surfaces: Definition and Examples, Finite Bordered Surfaces, Analytic and Meromorphic Functions on Surfaces: Definition and Examples, Harmonic Functions on Surfaces, Maximum Principles. The Uniformization Theorem: Green's Function of a Surface, Existence of Green's Function for Finite Bordered Surfaces, Symmetry of Green's Function, Bipolar Green's Function, The Uniformization Theorem, Covering Surfaces.
Reference materials
-
T. Gamelin: Complex Analysis, Springer-Verlag, New York, 2004.
-
C. Berenstein and R. Gay: Complex Variables. An Introduction, Springer-Verlag, New York, 1991.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH301 / Instructor's consent
Differentiable manifold, Tangent Spaces, Submanifolds, Immersions, Embeddings, Vector Fields, Riemannian Metric, Examples: Euclidean Metric & Hyperbolic Metric, Isometries and Local Isometries, Isometries of upper half plane. Affine connection, Covariant Differentiation, Parallel Vector Field, Parallel Transport, Levi-Civita Connection, Christoffel Symbols. Geodesics, Geodesics Flow, Exponential Map, Gauss Lemma, Normal Neighborhoods, Minimizing Properties of Geodesics, Convex Neighborhoods, Geodesics inhyperbolic plane. Curvature, Bianchi Identity, Sectional curvature. Jacobi Field, Jacobi Equation, Conjugate Points. Geodesic complete manifold, Hopf-Rinow theorem, Cartan Hadamard Theorem.
Reference materials:
-
M. P. Do Carmo: Riemannian Geometry, Birkhauser
-
William M. Boothby: An Introduction to Differentiable Manifolds and Riemannian Geometry, Academic Press
-
Kumaresan: Differential geometry and Lie groups, TRIM Series
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH301 / Instructor's consent
Recalling definition of homotopy and fundamental group. Van Kampen theorem.Free groups and Free product of groups. Fundamental groups of sphere, Wedgeof circles. CW-complexes definition and examples. Statement of classification of compact surfaces and polygonal representation. Computation of fundamental groups of compact surfaces. Homotopy extension property of a CW pair. Proof of the fact that if (X, A) has HEP and A contractible, then 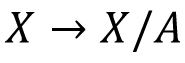 is a homotopy equivalence. Examples from Hatcher. Covering spaces, Path lifting, homotopy lifting, general lifting. Examples of covering of wedge of circles, circles. Universal cover and existence of covering, classification of covering by subgroups of fundamental groups. Deck transformation,action of fundamental group on Universal cover, normal covering. Applications: Subgroup of free group is free, Cayley complexes. Homology: Singular homology; Theory (long exact, homotopy invariance and statement of excision, Mayer vietoris and computation for sphere, statement of Universal Coefficients Theorem) Applications: Degree of sphere and applications, homology and fundamental groups. CW homology, some computations of homology of projective spaces and surfaces, Euler characteristic and cells/ Betti numbers. is a homotopy equivalence. Examples from Hatcher. Covering spaces, Path lifting, homotopy lifting, general lifting. Examples of covering of wedge of circles, circles. Universal cover and existence of covering, classification of covering by subgroups of fundamental groups. Deck transformation,action of fundamental group on Universal cover, normal covering. Applications: Subgroup of free group is free, Cayley complexes. Homology: Singular homology; Theory (long exact, homotopy invariance and statement of excision, Mayer vietoris and computation for sphere, statement of Universal Coefficients Theorem) Applications: Degree of sphere and applications, homology and fundamental groups. CW homology, some computations of homology of projective spaces and surfaces, Euler characteristic and cells/ Betti numbers.
Reference materials:
-
Hatcher: Algebraic Topology
-
Munkers: Algebraic Topology
-
Massey: Basic course in Algebraic Topology
-
Rotman: Algebraic Topology
-
Armstrong: Basic Topology
-
Bredon: Topology and Geometry
|
|
Credits:
|
9
|
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
The course includes a review of basic results from algebraic geometric objects, such as algebraic varieties and their properties; Motivation and definition of a toric variety and some basic examples; Affine toric varieties and their explicit constructions; Rational convex polyhedral cones; Affine toric varieties derived from cones; Points on affine toric varieties; Normality and smoothness of toric varieties; Projective toric varieties and examples, Projective toric varieties from monomial maps; Convex lattice polytopes; Very ample and normal polytopes,; Normal fans; Projective toric varieties from polytopes; Gluing affine varieties and abstract toric varieties; Toric varieties from fans; Limits of one-parameter subgroups; Orbit-cone correspondence; Orbit closures as toric varieties; Toric morphisms; Background on divisors; Weil divisors on toric varieties; Cartier divisors on toric varieties; Line bundles on toric varieties; Homogeneous coordinates on toric varieties; the construction of a toric variety as a Geometric Invariant Theory (GIT) quotient.
|
|
Syllabus:
|
Pre-requisite: None (Only for Ph.D. students of Statistics)
Least upper bound principle; limits, monotone sequences; subsequences, Bolzano-Weierstrass, Cauchy sequences, completeness; countable and uncountable sets; convergence of series, conditional convergence; equivalence of completeness of 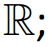 ; limsup, liminf, convergent series; absolute and conditional convergent, Riemann Rearrangement Theorem; convergence in ; limsup, liminf, convergent series; absolute and conditional convergent, Riemann Rearrangement Theorem; convergence in 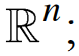 ; open sets and closed sets on ; open sets and closed sets on 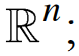 Cantor Intersection Theorem, Cantor set; limits and continuity; discontinuous functions; properties of continuous functions; uniform continuity; monotone functions; differentiation, Mean Value Theorem; Riemann integration; Fundamental Theorem of Calculus; sequence and series of functions, point wise convergence; uniform convergence, Weierstrass M-test, Dedekind test; uniform convergence and continuity; term by term integration and differentiation; power series; Taylor series, Weierstrass Approximation Theorem; analytic functions; Fourier series; differentiation of Cantor Intersection Theorem, Cantor set; limits and continuity; discontinuous functions; properties of continuous functions; uniform continuity; monotone functions; differentiation, Mean Value Theorem; Riemann integration; Fundamental Theorem of Calculus; sequence and series of functions, point wise convergence; uniform convergence, Weierstrass M-test, Dedekind test; uniform convergence and continuity; term by term integration and differentiation; power series; Taylor series, Weierstrass Approximation Theorem; analytic functions; Fourier series; differentiation of 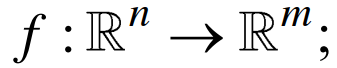 partial derivatives; chain rule; higher derivatives, local extrema; Taylor expansion; multiple integrals, determinant and volumes, Jacobians. partial derivatives; chain rule; higher derivatives, local extrema; Taylor expansion; multiple integrals, determinant and volumes, Jacobians.
Recommended books:
-
K.R. Davidson and A.P. Donsig: Real Analysis and Applications, Springer, 2010.
-
R.S. Strichartz: The Way of Analysis, Jones and Bartlet Mathematics, 2000.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 421 / Instructor's Consent
Volterra and Fredholm integral equations, Resolvent Kernels. Operator equations, Fredholm theory, Hilbert Schmidt theory. Nonlinear integral equations, Singular integral equation
Reference materials:
|
|
Credits:
|
9 |
|
Syllabus:
|
Pre-requisite: MTH 421 / Instructor's Consent
Elements of operator theory and Hilbert spaces; Introduction to the theory of distributions. Sobolev Spaces: Imbedding and compactness theorems, Fractional spaces and elements of trace theory. Applications to elliptic equations or parabolic equations
Reference materials:
|
|
Credits:
|
9 |
|
Syllabus:
|
Pre-requisite: MTH201 / Instructor's Consent
Basic results on system of linear equations, Cauchy-Binet formula for computing determinant, Rank factorization of a singular matrix, Vector Spaces associated with a matrix, Different types of generalized inverses, Moore-Penrose Inverse. Spectral Theorem of symmetric matrices, algebraic and geometric multiplicities, characteristic and minimal polynomials, Courant-Fischer Theorem, Interlacing theorems for eigenvalues, Quadratic forms, Positive definite matrices and its characterizations. Graphs, digraphs, examples, sub-graphs, simple graphs, emphasis on tree, cycle graph and complete graph/bipartite graphs, complement of a graphs, path, walk and cycle in a graph. Definition, example, rank and minor of {0, 1,-1}-incidence matrix, Substructure of a graph, Path-matrix and Moore-Penrose inverse of incidence matrix. Adjacency matrix, relationship with number of edge/walks/..., eigenvalues of certain graphs, Determinant in terms of cycles and edges, Bounds on the spectrum of adjacency matrix, Laplacian matrix of a graph, it's properties, Matrix Tree theorem, Bounds on Laplacian spectral radius, Perron Frobenius theory, Basic results on Regular and Strongly regular graphs, Algebraic connectivity, Fiedler's theorems, Bounds on algebraic connectivity.
Reference materials:
-
R. B. Bapat: Graphs and Matrices, TRIM Series, Hindustan Book Agency, New Delhi, 2010.
-
C. Godsil and G. Royle: Algebraic Graph Theory, GTM, Springer, 2001.
-
N. Biggs: Algebraic Graph Theory, Cambridge Mathematical Library, 2016.
|
|
Credits:
|
9 |
|
Syllabus:
|
Pre-requisite: MTH 421 / Instructor's Consent
Picard's theorem, Boundedness of solutions, Omega limit points of bounded trajectories. LaSalle's invariance principle; Stability via Lyapanov's indirect method, Converse Lyapanov functions, Sublevel sets of Lyapanov functions, Stability via Lyapanov's direct method, Converse Lyapanov's theorems, Brokett's theorem, Applications to control system; Stable and unstable manifolds of equilibria, Stable manifold theorem, Hartman Grobman theorem, Examples and applications, Center manifold theorem, Center manifold theorem, Normal form theory, Examples and applications to nonlinear systems and control; Poincare map, and stability theorems for periodic orbits; Elementary Bifurcation theory.
Reference materials:
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 405, MTH 424 / Instructor's Consent
Review of topics in Functional Analysis and Sobolev Spaces, Mapping between Banach Spaces, Degree theory, Bifurcation theory, Variation method, Constrained critical points, deformation and Palais condition, Linking thorems, Mountain pass theorem and Ekeland's variation principle.
Reference materials:
-
H. Brezis: Functional Analysis- Sobolev and Partial Differential Equations, Universitext Springer
-
L. Nirenberg: Topics in Nonlinerar Functional Analysis, Courant Institute of Mathematical Sciences.
-
D. G. De Figueiredo: The Ekeland Variational Principle with Applications and Detours, TIFR Lecture Notes.
-
A. Ambrosetti and A. Malchiodi: Nonlinear Analysis and Semilinear Elliptic Problems, Cambridge University Press.
|
|
Credits:
|
9
|
Credits
3-0-0-0(9)
Prerequisites
Prerequisites: Instructor’s consent.
Aims of the course
The concept of a Grothendieck topos was introduced in the pioneering work of A. Grothendieck in algebraic geometry to provide a vast generalization of the concept of a sheaf on a topological space. The course will introduce students to the definition and properties of sheaves, not only on topological spaces but also on sites. A Grothendieck topos is a category of sheaves on a site, and possesses very rich category-theoretic structure. Although the course will mostly deal with sheaves of sets, sheaves of abelian groups and rings etc. will also be introduced on the way. The language of category theory necessary for the course will be introduced at the start.
Syllabus
- Categorical preliminaries: category, morphisms, functor, natural transformation, universal constructions, adjoint functors, limits and colimits, exponentials.
- Functor categories: limits and colimits, subobject classifiers.
- Lattices and algebras: lattices, distributive lattices, implication, negation,Boolean algebra, Heyting algebra, subobject lattices in functor categories.
- Logic: interpretation of logical connectives in functor categories, quantifiers as adjoints.
- Sheaves on topological spaces: definition of sheaves, subsheaves, sieves,germ, stalk, bundles, cross-section, sheaves with algebraic structure, inverse image sheaves.
- Grothendieck topologies: generalized neighbourhood, sites, the Zariskisite, sheaves on a site, Grothendieck topos, associated sheaf functor.
- Properties of Grothendieck toposes: limits, colimits, exponentials, subobject classifier.
- Characterization of Grothendieck toposes: Elementary toposes, Giraud’stheorem.
References
- MacLane, Categories for the working mathematician, Vol. 5, Springer Science & Business Media, 2013.
- MacLane and I. Moerdijk, Introduction to sheaves in geometry and logic: A first introduction to topos theory, Springer Science and Business media, 2012.
- Kashiwara and P. Schapira, Categories and sheaves, Vol. 332, Springer Science & Business Media, 2005.
- P.T. Johnstone, Sketches of an elephant: A topos theory compendium, Vol. 1 and 2, Oxford University Press, 2002.
|
Syllabus:
|
Pre-requisite: (MTH 201 or MTH204) or Instructors Consent.
Theory of bilinear forms on vector spaces over arbitrary fields, isometry groups, Lie structure on the tangent spaces of isometry groups, revision of Lie algebras, semisimple Lie algebras, Chevalley basis, Cartan-Weyl classifica+on of semisimple Lie algebras, universal enveloping algebras, PBW, integral structures in Lie-algebras, construc+on of Chevalley groups, commuta+on rela+ons, classifica+on of Chevalley groups, automorphisms of Chevalley groups, introduc+on to elementary theory of schemes, chevalley groups as algebraic groups, Borel subgroups, Tori, Root datum and classifica+on of semisimple algebraic groups over algebraically closed fields.
Reference materials:
-
Hermann Weyl, Classical groups.
-
R. Steinberg, Lectures on Chevalley groups, Lecture notes in Mathema+cs of AMS.
-
A. Borel Linear algebraic groups GTM.
-
Herman Weyl, Symmetry Princeton Science library.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite(s): MTH 424/ Instructor's Consent
Introduction to Semigroups, C0-semigroups, Hille-Yosida result, Heat equation, Wave equation, Inhomogeneous equations, Techniques for nonlinear problems, Palais-Smale Condition, Mountain Pass theorem, Hamilton Jacobi equations, Viscosity Solutions.
|
|
Credits:
|
9
|
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Introduction Approximate Statistical Procedures; Asymptotic Optimality Theory Review of Stochastic Convergence Basic Theory, Stochastic and 0 Symbols, Characteristic Functions; AlmostSure Representations, Convergence of Moments, Convergence Determining Classes; Law of the Iterated Logarithm, Lindeberg Feller Theorem, Convergence in Total Variation Delta Method Basic Result, Variance Stabilizing Transformations; Higher Order Expansions, Uniform Delta Method; Moments M and Z Estimators Introduction; Consistency; Asymptotic Normality; Estimated Parameters, Maximum Likelihood Estimators, Classical Conditions, OneStep Estimators; Rates of Convergence; Argmax Theorem W. Contiguity Likelihood Ratios; Contiguity. Local Asymptotic Normality Introduction, Expanding the Likelihood Convergence to a Normal Experiment, Maximum Likelihood; Limit Distributions under Alternatives; Local Asymptotic Normality. Stochastic Convergence in Metric Spaces Metric and Normed Spaces; Basic Properties; Bounded Stochastic Processes. Empirical Processes Empirical Distribution Functions; Empirical Distributions; Goodness of Fit Statistics; Random Functions; Changing Classes; Maximal Inequalities Functional Delta Method von Mises Calculus; Hadamard Differentiable Functions; Some Examples Bootstrap Introduction, Consistency; Higher Order Correctness W.
|
Credits
3-0-0-0(9)
Prerequisites
Prerequisites: Instructor’s consent.
Syllabus
- Structure vs. property: monoids, groups, preorders, partial orders; structure preserving maps: homomorphisms, continuous maps; category; homsets and duality; functor-covariant and contravariant; natural transformations.
- Small, locally small and large categories; set theory vs category theory;Russell’s paradox and the category of all categories; skeletons and axiom of choice.
- Isomorphism; groupoid; monomorphism and epimorphism; full, faithful,essentially surjective functors, equivalence of categories; building even more categories from the old ones: slice categories and local property, comma categories, functor categories, congruence and quotients.
- Representable functors; Yoneda lemma and Yoneda embedding; separating and detecting families; injective and projective objects; representables are projective.
- Adjunctions: definition and examples; initial and terminal objects; relation to comma categories; composition of adjoint functors; units, counits and characterization of adjoint functors; equivalence gives adjoint functors.
- Categorical properties: initial and terminal objects, products, coproducts;diagrams and (co)cones; (co)limits of a given shape; (co)equalizers, regular mono(epi)morphisms; pullbacks and pushouts; direct and inverse limits.
- Constructing all (co)limits from some of them; (co)complete categories;absolute (co)limits; preservation, creation and reflection of (co)limits; right adjoints preserve limits.
- General adjoint-functor theorem; well-powered categories; special adjointfunctor theorem; examples.
- Definition of monads; monads arising from adjunctions; algebras for amonad; Eilenberg-Moore category; Kleisli category; Kleisli is initial while Eilenberg-Moore is terminal.
- Monadic functors; Beck’s monadicity theorem; Crude monadicity theorem;examples.
- Special categories and applications: toposes, additive and abelian categories, symmetric monoidal categories, model categories.
References
- MacLane, Categories for the working mathematician, Vol. 5, Springer Science & Business Media, 2013.
- Awodey, Category theory, Oxford University Press, 2010.
- Kashiwara and P. Schapira, Categories and sheaves, Vol. 332, Springer Science & Business Media, 2005.
- Ad´aamek, H. Herrlich and G. E. Strecker, Abstract and concrete categories–The joy of cats, 2004.
- F. Borceaux, Handbook of categorical algebra 1: Basic category theory, Vol. 50, Encyclopedia of Mathematics and its Applications, 1994.
|
Syllabus:
|
Pre-requisite: MTH611/612/613
Background from commutative algebra: Local rings, localizations, primary decomposition, Integral extensions, integral closures. Algebraic geometry: Affine algebraic sets, Hilbert Nullstellansatz, Projective algebraic sets, projective Nullstellansatz, Affine varieties, structure sheaf, Prevarieties, varieties, morphisms, Affine and projective algebraic sets are varieties, dimension of varieties, products of varieties, images and fibers of morphisms, Tangent spaces, differential of a morphism, Smooth morphisms, smooth varieties, complete varieties. Algebraic Groups: Basic definitions and examples, Lie algebra of an algebraic group, Linear representations of algebraic groups, Affine algebraic groups are linear; connected projective algebraic groups are abelian varieties, rigidity of abelian varieties, quotients, Homogeneous spaces, Chevalley's theorem on algebraic groups (without proof).
Reference materials:
-
M. F. Atiyah and I. G. MacDonald: Introduction to commutative algebra.
-
Michel Demazure and Peter Gabriel: Introduction to algebraic geometry and algebraic groups.
-
T. A Springer: Linear Algebraic Groups.
-
Armand Borel: Linear Algebraic Groups.
-
David Mumford: Abelian varieties.
-
R. Hartshorne: Algebraic Geometry.
|
|
Credits:
|
9
|
Units
3-0-0-0-[9]
Prerequisites
Complex analysis (MTH 403), abstract algebra (MTH204)/Consent of the instructor.
Course Description
Analytic number theory is a major branch of number theory. One of the basic theme of analytic number theory is that the study of distribution of prime numbers is deeply related with some complex analytic properties of certain Dirichlet series. The main goal of this introductory course is to study two fundamental theorems under this theme- (i) Dirichlet Theorem on Primes in Arithmetic Progression: This theorem discusses how the distribution of primes numbers in an A.P. is related to the non-vanishing of certain Dirichlet L-function. (ii) The Prime Number Theorem: This theorem relates the natural density of primes with the behaviour of the Riemann Zeta function on the line Re(s) =1 in the complex plane. We will also introduce modular forms and the associated Lfunctions. Modular forms are certain analytic functions defined on the upper half of the complex plane which have many symmetries with respect to the matrix group SL2(Z). Given a ’nice’ modular form one can naturally associate an L-function, which can also be expressed as a Dirichlet series on the complex plane. The L-function of a modular form is a central object of study in number theory both from analytic as well as arithmetic point of view.
Course Contents
- Arithmetical functions
- Distribution of prime numbers; some elementary estimates.
- Characters of finite abelian groups.
- Riemann Zeta function and Dirichlet L-functions.
- Dirichlet’s Theorem on primes in arithmetic progression.
- Prime Number Theorem.
- Modular forms (for SL2(Z)) and their L-functions.
- (If time permits) Prime number theorem for arithmetic progressions, exponential sums.
References
- Introduction to Analytic Number Theory, T.M. Apostol, UTM, SpringerVerlag 1976.
- Multiplicative Number Theory, H. Davenport, GTM 74, Springer-Verlag.
- Problems in Analytic Number Theory, M. Ram Murty, GTM 206, Springer-Verlag.
- Multiplicative Number Theory I, H. L. Montgomery and R C Vaughan,Cambridge Studies in Advance Math. 97.
- A course in Arithmetic, J. P. Serre, GTM 07, Springer-Verlag.
- Introduction to elliptic curves and modular forms, N. Koblitz, GTM 97,Springer-Verlag.
Credits
3-0-0-0 (9)
Prerequisites
It will be assumed that audience has enough familiarity with measure and integration, Bounded linear operators, Hilbert spaces.
Aimed at
PhD and M.Sc. Students; however interested B.S. students can be considered in a case by case basis by the instructor.
Course description
During the last four decades, it has been realized that some significant problems in number theory can be solved using techniques from the theory of dynamical systems. This influential approach has lead us to one of the forefronts of modern mathematical research. Our course aims to convey the central concepts and basic techniques of the theory to the students and to develop their background to pursue further. The course will be self contained. We shall begin from scratch and work out the details.
Course contents
Broadly the following topics are covered in details with varieties of examples and applications to metric umber theory:
Measure preserving transformation and its examples, Recurrence properties, Topological dynamics, Conditional expectations, Main ergodic theorems, Subadditive ergodic theorem, Ergodicity and its examples, Spectral approach to ergodicity, various applications of Birkhoff’s individual ergodic theorem, Mixing and its examples, Equidistribution, Unique ergodicity, Weyl’s theorem on equidistribution of polynomials, Ergodic measures are precisely the extreme points, Existence and uniqueness of conditional probability measures, Ergodic decomposition.
If time permits, we may discuss several connections between Diophantine approximation and diagonal flows on the space of lattices and some recent developments.
References
- Bekka, M. Bachir; Mayer, Matthias. Ergodic theory and topological dynamics of group actions on homogeneous spaces, London Mathematical Society Lecture Note Series, 269. Cambridge University Press, Cambridge, 2000.
- Einsiedler, Manfred; Ward, Thomas. Ergodic theory with a view towards number theory, Graduate Texts in Mathematics, 259. Springer-Verlag London, Ltd., London, 2011. ISBN: 978-0-85729-020-5.
- Furstenberg, H. Recurrence in ergodic theory and combinatorial number theory. M. B. Porter Lectures. Princeton University Press, Princeton, N.J. ISBN: 0-691-08269-3.
- Katok, Anatole; Hasselblatt, Boris. Introduction to the modern theory of dynamical systems, With a supplementary chapter by Katok and Leonardo Mendoza, Encyclopedia of Mathematics and its Applications, 54. Cambridge University Press, Cambridge, 1995. ISBN: 0-521-34187-6.
- Parry, William. Topics in ergodic theory, Cambridge Tracts in Mathematics, 75. Cambridge University Press, Cambridge-New York, 1981. ISBN: 0-521-22986-3.
- Pollicott, Mark, Yuri, Michiko. Dynamical systems and ergodic theory, London Mathematical Society Student Texts, 40. Cambridge University Press, Cambridge, 1998. ISBN: 0-521-57294-0; 0-521-57599-0.
- Walters, Peter. An introduction to ergodic theory, Graduate Texts in Mathematics, 79. Springer-Verlag, New York-Berlin, 1982. ISBN: 0-38790599-5.
- Zimmer, Robert J. Ergodic theory and semisimple groups, Monographs in Mathematics, 81. Birkh¨auser Verlag, Basel, 1984. ISBN: 3-7643-3184-4.
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Harmonic functions and their basic properties; The Dirichlet problem on the unit disc; Positive Harmonic Functions, Harnack’s inequality and Harnack distance; Subharmonic functions; Maximum principle, Phragmen-Lindelof principle, Liouville’s Theorem; Criterion for subharmonicity and Integrability; Convexity property of subharmonic functions and smoothing; Potentials and energy corresponding to it; Existence of equilibrium measure; Upper semicontinuous regularization, the Brelot-Cartan theorem; Minus infinity sets and removable singularities, the Rado-Stout theorem; Generalized Laplacians; Solution of the Dirichlet problem; Criterion for regularity; Harmonic measure; Green’s functions and its properties and Riemann mapping theorem; The Poisson Jensen formula for subharmonic functions and its applications; Introduction to Capacity and computing capacity.
|
|
Syllabus:
|
Pre-requisite: MTH 304, MTH 611
p-adic numbers: non-Archimedean absolute values, valuations, Ostrowski theorem, Cauchy sequences, p-adic integers, completions, Hensel's lemma, structure of  and and 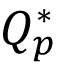 . Quadratic forms: definition of quadratic forms and bilinear forms, equivalence of quadratic forms, local-global principle (Hasse-Minkowski theorem), rational points on conics. Infinite Galois Theory: Profinite groups and profinite topology, Infinite Galois extensions and Galois group as profinite groups, absolute Galois groups, the fundamental theorem of Galois theory (for infinite extensions), absolute Galois group of finite fields, Frobenius automorphism, absolute Galois group of . Quadratic forms: definition of quadratic forms and bilinear forms, equivalence of quadratic forms, local-global principle (Hasse-Minkowski theorem), rational points on conics. Infinite Galois Theory: Profinite groups and profinite topology, Infinite Galois extensions and Galois group as profinite groups, absolute Galois groups, the fundamental theorem of Galois theory (for infinite extensions), absolute Galois group of finite fields, Frobenius automorphism, absolute Galois group of 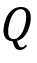 and and 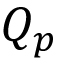 . Geometry of curves over . Geometry of curves over 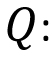 Affine Varieties and projective varieties, curves and function fields, divisors on curves, the Riemann-Roch theorem (statement without proof), Elliptic curves over Affine Varieties and projective varieties, curves and function fields, divisors on curves, the Riemann-Roch theorem (statement without proof), Elliptic curves over 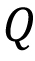 , Group law on elliptic curves, Weierstrass equations, action of the absolute Galois group of , Group law on elliptic curves, Weierstrass equations, action of the absolute Galois group of 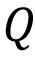 over over 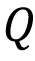 points of elliptic curves, Weak Mordell-Weil Theorem, Mordell-Weil Theorem, Faltings' Theorem (statement without proof). points of elliptic curves, Weak Mordell-Weil Theorem, Mordell-Weil Theorem, Faltings' Theorem (statement without proof).
Reference materials:
-
Neal Koblitz: p-adic numbers, p-adic analysis and zeta-functions, 2nd ed, GTM, vol 58, Springer-Verlag.
-
Serge Lang: Algebra, 3rd ed, GTM, Vol. 211, Springer-Verlag.
-
J.-P. Serre: A course in arithmetic, Springer-Verlag, 1973, Translated from French; GTM, No. 7.
-
Joseph H. Silverman, The arithmetic of elliptic curves, GTM, vol. 106, Springer-Verlag, 1992. Corrected reprint of the 1986 original.
-
William Fulton, Algebraic Curves: An Introduction to Algebraic Geometry, 2008,
http://www.math.lsa.umich.edu/wfulton/CurveBook.pdf.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite(s): MTH 301, MTH 404/ Instructor's Consent
Harmonic analysis on 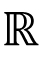 : Fourier Transform, basic properties, inversion formula, Plancherel formula, Paley-Wiener theorem, Young's inequality. Tangent space of : Fourier Transform, basic properties, inversion formula, Plancherel formula, Paley-Wiener theorem, Young's inequality. Tangent space of  , inner product on the tangent spaces of , inner product on the tangent spaces of  , ,  as a Riemannian symmetric space, geodesics on as a Riemannian symmetric space, geodesics on  , horocycles. Iwasawa decomposition, Cartan decompostion of , horocycles. Iwasawa decomposition, Cartan decompostion of 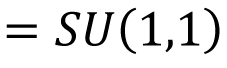 , Haar measures in these decompositions, unimodular group. Laplace-Beltrami operator on , Haar measures in these decompositions, unimodular group. Laplace-Beltrami operator on  and its eigenfunctions, the Helgason-Fourier transform, Radon transform, elementary spherical functions, spherical transform, Abel transform, assymptotics of elementary spherical functions. Inversion and Plancherel formula for Helgason-Fourier transform, Paley-Wiener theorem, Helgason-Johnson's theorem, Kunze-Stein phenomena. and its eigenfunctions, the Helgason-Fourier transform, Radon transform, elementary spherical functions, spherical transform, Abel transform, assymptotics of elementary spherical functions. Inversion and Plancherel formula for Helgason-Fourier transform, Paley-Wiener theorem, Helgason-Johnson's theorem, Kunze-Stein phenomena.
Reference material(s):
-
R. Gangolli, and V. S. Varadarajan: Harmonic analysis of spherical functions on real reductive groups, Ergebnisse der Mathematik und ihrer Grenzgebiete [Results in Mathematics and Related Areas], 101. Springer-Verlag, Berlin, 1988.
-
S. Helgason: Topics in harmonic analysis on homogeneous spaces, Progress in Mathematics, 13. Birkhäuser, Boston, Mass., 1981.
-
S. Helgason: Groups and geometric analysis, Integral geometry, invariant differential operators, and spherical functions. Mathematical Surveys and Monographs, 83, AMS, Providence, RI, 2000.
-
S. Helgason: Geometric analysis on symmetric spaces, Second edition. Mathematical Surveys and Monographs, 39, AMS, Providence, RI, 2008.
-
R. A. Kunze and E. M. Stein: Uniformly bounded representations and harmonic analysis of the 2x2 real unimodular group, Amer. J. Math. 82, 1—62, 1960.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MSO201 / Instructor's consent
Brief review of simple and multiple linear regression along with the outlier detection methods. Basic idea of non-parametric regression. Measures of robustness in different statistical problems (e.g., the influence function and the breakdown point). Least squares and least absolute deviations in regression model; Least median squares and least trimmed squares estimators; Different statistical properties and the computational algorithms of the robust estimators of the location and the scale parameters (for the univariate as well as the multivariate data); Robust measure of association and robust testing of hypothesis problems. Data-depth and the robust estimators based on the data-depth; Multivariate quantiles and its properties along with the computational algorithm; Possible extension of the depth-based and the quantile-based estimators for the functional data. Some applications of robust estimators (e.g., robust classification and cluster analysis), Robust model selection problems.
Reference materials:
-
P J Rousseeuw and A M Leroy: Robust Regression and Outlier Detection, Wiley, 2003
-
P J Huber: Robust Statistics, Wiley 2009
-
A W van der Vaart: Asymptotic Statistics, 2000
-
R J Serfling: Approximation Theorems of Mathematical Statistics, Wiley, 2002
-
B. W. Silverman: Density Estimation for Statistics and Data Analysis, Chapman and Hall, 1999
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite(s): MTH 405/ Instructor's Consent
Existence of Minimizer, Perron's Method variational form, Concentration-Compactness, Ekeland's Variational Principle, Palais-Smale Condition and Mountain Pass theorem, Application to semilinear equation with symmetry, Krasnoselskii Genus, Ljusternik-Schinelman Category, Multiple critical points of even functional on symmetric manifolds, Pohozaev Non-Existence Result, Brezis-Nirenberg result, Nehari Manifold and Fibering Method, Alexandrov's Moving Plane and Berestycki Sliding Method.
Reference material(s):
-
Michel Willem: Minimax Theorems, Birkhauser
-
A. Ambrosetti and G. Prodi: A primer of Nonlinear Analysis, Cambridge studies in advanced mathematics.
-
A. Ambrosetti and A. Malchiodi: Nonlinear Analysis and semilinear elliptic problems, Cambridge studies in advanced mathematics.
|
|
Credits:
|
|
|
Syllabus:
|
Pre-requisite(s): MTH 201, MTH 304, MTH 305/ Instructor's consent
Definition of manifolds and the fundamental ideas connected with them: Local coordinates, topological manifolds, differentiable manifolds, tangent spaces, vector fields, integral curves of vector fields and one-parameter group of local transformations, define manifold with boundary and orientation of a manifold. Differential forms on differentiable manifolds: Differential forms on Euclidean n-spaces and on a general manifold, the exterior algebra, Interior product and Lie derivative, The Cartan formula and properties of Lie derivatives. Frobenius theorem. The de Rham Theorem: Homology of manifolds, Integral of differential forms and the Stokes theorem. de Rham cohomology, The de Rham theorem. Applications of the de Rham theorem; Hopf invariant, the Massey product, cohomology of compact Lie groups, Mapping degree, Integral expression of the linking number by Gauss. Differential forms on Riemannian manifolds: The *- operator of Hodge, Laplacian and harmonic forms. The Hodge theorem and the Hodge decomposition of differential forms. Applications of the Hodge theorem.
Reference material(s):
-
Shigeyuki Morita: Geometry of Differential Forms, Volume 201, Translations of Mathematical Monographs, AMS, Providence, RI, 2001. (Indian edition 2009).
-
Frank W. Warner: Foundations of differentiable manifolds and Lie groups, volume 94 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1983.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 416A/ Instructor's Consent
Brief review of topics in Multiple Linear Regression Analysis; Econometric tests on Heteroscedasticity and Autocorrelation; Restricted Regression; Errors in Variables; Functional Form and Structural Change; Stochastic Regressors; Instrumental Variable (IV) Estimation; Large Sample Properties of Least Square and IV estimators; Panel Data Models; Systems of Regression Equations -Seemingly Unrelated Regression Equations (SURE) & Multivariate Multiple Linear Regression; Simultaneous Equation Models - Structural and Reduced forms, Rank and Order conditions for Identifiability, Indirect Least Squares, 2-stage Least Squares and Limited Information Maximum Likelihood methods of estimation, k-class estimators and Full Information Maximum Likelihood Estimation; Models with lagged variables - Autoregressive Distributed Lag (ARDL) Models and Vector Autoregressive (VAR) Models; Topics on Econometric Time Series Models - Autoregressive and Generalized Autoregressive Conditionally Heteroscedastic (ARCH & GARCH) Models, Unit Root, Co-integration and Granger Causality.
|
|
Credits:
|
9
|
Credits
3-0-0-0(9)
Prerequisites
Prerequisites: Instructor’s consent.
Aims of the course
Combinartorics is an area of mathematics that, at elementary level, deals with problems in counting/enumeration, especially in the realm of finite sets. However the supply of problems as well as the methods to solve them come from a variety of domains of mathematics ranging from algebra, analysis, number theory, geometry, probability theory and so on. Leon Mirsky has rightly said: ”combinatorics is a range of linked studies which have something in common and yet diverge widely in their objectives, their methods, and the degree of coherence they have attained”.
This course will introduce techniques from three popular branches of combinatorics that are of areas of active research currently, namely extremal combinatorics, extremal graph theory and additive combinatorics over dyadic groups. The emphasis will be on the techniques than the solutions of the problems.
Syllabus
- Extremal combinatorics with set systems: Hall’s marriage theorem, Sperner’slemma, Lubell-Yamamato-Meshalkin inequality, Kruskal-Katona theorem, Erdos-Ko-Rado theorems.
- Extremal graph theory: Mantel’s theorem, Turan’s theorem, Dirac’s theorem, Erdos-Stone-Simonovits theorem, Szemeredi’s regularity lemma, Triangle removal lemma, Roth’s theorem for 3 term arithmetic progressions.
- Additive combinatorics with dyadic groups: Discrete Fourier transform,Plancherel’s theorem, Bogolyubov’s lemma, Arithmetic regularity and removal lemmas, Coincidence of algebraic and statistical independence of Bernoulli r. v.s, Rudin’s inequality, Sets with small sumsets: Rusza’s covering lemma, Freiman’s theorem.
References
- Bollob´as, B´ela. Combinatorics: set systems, hypergraphs, families of vectors, and combinatorial probability. Cambridge University Press, 1986.
- Bollob´as, B´ela. Extremal graph theory. Courier Corporation, 2004.
- Tao, Terence, and Van H. Vu. Additive combinatorics. Vol. 105. Cambridge University Press, 2006.
|
Syllabus:
|
Pre-requisite: Instructor's Consent
Examples from nature and laboratory, Role of spatio-temporal models in biology. Linear Stability analysis: Formulation, Normal modes, Application to system of one, two and more variables. Bifurcation analysis: Introduction, Saddle-node, Pitchfork, Transcritical, Hopf and Hysteresis bifurcations. Spatial pattern formation: Reaction-diffusion system, Turing instability, Pattern formation in reaction-diffusion system. Chemotaxis: Introduction, Modelling chemotaxis, Linear and Nonlinear analysis. Tumor modelling: Introduction, Models of tumor growth, Moving boundary problems, Response of immune system. Numerical simulation of Spatio-temporal model: Introduction, Finite-difference techniques, Monotone methods.
|
|
Credits:
|
9
|
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Gelfand-Naimark theory, Commutative C*-algebras, Representations of C*-algebras, The spectral theorem, Polar decomposition, Compact operators, The three locally convex topologies, the GNS representation, Geometry of projections, Preduals and W*-algebras, Group von Neumann algebras, Group measure space construction, Crossed product algebras, vonNeumann's bicommutant theorem, Bounded Borel functional calculus, The Kaplansky density theorem, Normality and W*-algebras.
|
|
Syllabus:
|
Pre-requisite: MSO 201 / Instructor's Consent
Decision function, Risk function, Optimal decision rules, Admissibility &completeness, The minimax theorem, The complete class theorem, Sufficient statistics. Invariant decision problems, Admissible & minimax invariant rules, The Pitman estimates, Estimation of a distribution function
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MSO 201 / Instructor's Consent
Basic distribution theory, Moments of order statistics including recurrence relations, Bounds and approximations, Estimation of parameters, Life testing, Short cut procedures, Treatment of outliers, Asymptotic theory of extremes.
|
|
Credits:
|
9
|
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Order statistics, Tests of goodness of fit, Sign & signed rank tests, WaldWolfowitz, Kolmogorov Smirnov, Median & MannWhitney tests, Linear ranktests for the location problem & scale problem, Measures of association, Asymptotic relative efficiency.
|
|
Syllabus:
|
Pre-requisite: MSO 201 / Instructor's Consent
Introduction to simulation & Monte-Carlo studies; Generation of random variables. Interactive computational & graphical techniques in model building; Data based inference methods such as JackKnife, Bootstrap and cross validation techniques; Use of statistical packages in data analysis
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MSO 201 / Instructor's Consent
Linear stationary processes, Auto covariance & spectral density functions &moving average processes, Linear non-stationary processes, Model estimation& identification, Forecasting, Transfer function models, Design for discrete control
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MSO 201 / Instructor's Consent
Estimation methods, Commonly encountered problems in estimation, Statistical inference, Multi-response nonlinear model, Asymptotic theory, Computational methods.
Reference materials:
|
|
Credits:
|
9
|
units
3-0-0-0-[9]
Prerequisites
(i) MTH 204a (Algebra-I), (ii) MTH 403a (Complex Analysis) and (iii) consent of the instructor.
Course Description
This aim of this course is to get introduced to certain important topics in number theory; both from arithmetic and analytic side. The topics include Zeta functions and L-functions, modular forms, quadratic forms, study of polynomial equations over finite fields. These topics have application in various other traditional branches of mathematics and also in computer science and physics. On the arithmetic side, we will begin with the study of polynomial equations over finite fields and the law of quadratic residue. We will then move into the p-adic world. Theory of quadratic forms over rational numbers, p-adic numbers, finite fields and the interrelation between them will be studied. On the analytic side, we will introduce Riemann Zeta function and more generally Dirichlet L-functions. We will discuss the significance of analytic properties of these functions in theorem on primes in arithmetic progression and prime number theorem. We will briefly discuss some basic properties of modular forms (for SL2(Z)). The relation between elliptic curves and modular forms will be outlined.
Course Contents
- Review of finite fields, polynomial equations over finite fields; ChevalleyWarning theorem.
- Quadratic residue; law of quadratic reciprocity.
- p-adic numbers and p-adic inegers. Hensel’s Lemma.
- Quadratic forms (over Q, Qp and Fp).
- Riemann Zeta function and (Dirichlet) L-functions.
- Dirichlet’s theorem on primes in arithmetic progression, prime numbertheorem.
- Modular forms (for SL2(Z)); relation with elliptic curves.
References
- A course in Arithmetic, J. P. Serre, GTM 07, Springer-Verlag.
- Problems in Analytic Number Theory , M. Ram Murty, GTM 206, Springer-Verlag.
- A first course in Modular forms, F. Diamond and J. Shurman, GTM 228, Springer-Verlag.
- Multiplicative Number Theory, H. Davenport, GTM 74, Springer-Verlag.
- Algebraic Number Theory, J. Neukirch, Grundlehren der MathematischenWissenschaften 322, Springer-Verlag.
- p-adic Numbers, an introduction, F. Gouvea, Universitext, Springer-Verlag.
- Quadratic and Hermitian forms, W. Scharlau, Grundlehren der Mathematischen Wissenschaften 270, Springer Verlag.
Prerequisite:
None
Credits:
L-T-P-D
3-0-0-0
Total credits: 9
Summary:
Generalized inverse, Eigen values & canonical reduction of matrices, Least square theory, Regression analysis. Unified theory of least squares, Variance component estimation, Minimum mean square error estimation & ridge regression, Generalised linear and non-linear models.
References:
- Montgomery, D. C., Peck, E. A., and Vining, G. G. (2012). Introductionto Linear Regression Analysis. John Wiley & Sons, Hoboken, New Jersey, 5th edition.
- Hosmer, D. W. and Lemeshow, S. (2000). Applied Logistic Regression.John Wiley & Sons.
- Douglas M. Bates and Donald G. Watts (1988). Nonlinear RegressionAnalysis and Its Applications. John Wiley & Sons, Inc.
Credits
3-0-0-0 (9)
Prerequisites
MTH309: Probability Theory or MSO201A: Probability and Statistics, consent of the instructor.
Objectives
This course will present different methods of statistical pattern recognition for multivariate data, and use results from probability theory to study their asymptotic properties.
Syllabus
Results of convergence in almost sure sense and in probability, DCT, Basic inequalities, Conditional expectation, Methods of re-sampling. Introduction to discriminant analysis. Bayes’ risk, and its properties. Distance measures for density functions, and its relation with Bayes’ risk. Empirical Bayes’ risk and its convergence.
Parametric methods: Maximum likelihood principle, Fisher’s linear discriminant function (LDA), quadratic discriminant analysis (QDA). Consistency results. Logistic regression, Linear support vector machines (SVM), Maximum linear separation and Projection pursuit.
Non-parametric methods: Kernel discriminant analysis (KDA), nearest neighbor classification (kNN). Universal consistency results. Idea of curse of dimensionality, and the use of dimension reduction techniques like random projections, principal component analysis, etc.
Semi-parametric methods: Mixture Discriminant Analysis (MDA), Non-linear SVM, Hybrid classifiers, Classification using data depth. Related consistency results.
References
- Pattern Classification by Richard Duda, Peter Hart and David Stork.Wiley.
- A Probabilistic Theory of Pattern Recognition by Luc Devroye, L´aszl´oGy¨orfi and G´abor Lugosi. Springer.
- The Elements of Statistical Learning: Data Mining, Inference, and Prediction by Trevor Hastie, Robert Tibshirani, Jerome Friedman. Springer.
Credits
3-0-0-0 [9]
Prerequisites
MTH309 Probability Theory or equivalent, MTH433A Real Analysis or equivalent
Syllabus
- Preliminaries: Different Modes of Convergence, Law of Large Numbers,Motivations. (6 Lectures)
- Function classes and their complexities, Glivenko-Cantelli class of functions. (8 Lectures)
- Symmetrization, Concentration Bounds. (4 Lectures)
- Vapnik-Cervonenkis (VC) classes of functions, Covering and Bracketingnumbers, Examples: M-estimators. (8 Lectures)
- Donsker class, Uniform Central Limit Theorem, Examples. (6 Lectures)
- Arg-min continuous mapping theorem, Applications in Statistics: M-estimators,Lasso, Bootstrap consistency etc. (6 Lectures)
- More on Concentration Bounds/ Weak Convergence on Polish Spaces. (4 Lectures)
References
- W. van der Vaart and Jon A. Wellner. (1996). Weak Convergence and Empirical Processes, with Applications to Statistics. Springer Series in Statistics.
- Michael R. Kosorok. (2008). Introduction to Empirical Processes and Semiparametric Inference. Springer Series in Statistics.
- Sara van de Geer. (2009). Empirical Processes in M-Estimation. Cambridge Series in Statistical and Probabilistic Mathematics.
- Richard M. Dudley (2014). Uniform Central Limit Theorems. Cambridge Studies in Advanced Mathematics.
- G´abor Lugosi, Pascal Massart, and St´ephane Boucheron (2014). Concentration Inequalities: A Nonasymptotic Theory of Independence. Oxford University Press.
- Zhengyan Lin and Zhidong Bai. (2010). Probability Inequalities. Springer.
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Galerkin, Collocation & Tau methods, Spectral approximation, The Fourier system, Continuous & discrete Fourier expansion, Orthogonal polynomials in (1,1), Fundamentals of spectral methods for PDEs, Temporal discretization, The Galerkin Collocation method, Implicit spectral equations, Case of nonsmooth solutions.
|
|
Syllabus:
|
Pre-requisite: None (Only for MS students)
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: None (Only for MS students)
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: None (Only for MS students)
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: None (Only for MS students)
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH302 / Instructor's Consent
Modal Propositional Logic - Models and Frames, Consequence relations, Normal modal systems. Invariance results for models, Bisimulations, Finite model property, Translation into First order logic. Frame definability and Second order logic, Definable and undefinable properties. Completeness, Applications. Algebraic Semantics - Lindenbaum-Tarski Algebras, Jonsson-Tarski Theorem, Duality, Goldblatt-Thomason Theorem. Modal Predicate Logic - Axiomatization, Barcan formula, Soundness and Completeness, Expanding domains; Identity. Examples of some other modal systems and applications - Temporal logic with Since and Until, Multi-modal and Epistemic Logics. Non-normal modal logics. Neighbourhood semantics.
Reference materials:
-
P. Blackburn, M. de Rijke and Y. Venema: Modal Logic, Cambridge Tracts in Theoretical Computer Science, 2001.
-
G.E. Hughes and M.J. Cresswell: A New Introduction to Modal Logic, Routledge, 1996.
-
B.F. Chellas: Modal Logic, Cambridge University Press, 1980.
-
M. Fitting and R.L. Mendelsohn: First Order Modal Logic, Kluwer, 1998.
|
|
Credits:
|
9
|
Credits
3-0-0-0 (9)
Aimed at
PhD and M.Sc. Students; however interested B.S. students can be considered in a case by case basis by the instructor.
Prerequisites
consent of the instructor.
Syllabus
Some motivations from Probability theory for such spaces. Introduction of the Fractional Sobolev spaces. Definition via Fourier transform on Rn. Density results, Extension Theorem. Compact Embeddings Theorems. Holder Regularity Results. Fractional Poincar´e Inequality, Fractional Sobolev and Hardy’s Inequality. Fractional Poincar´e Inequality, Fractional Sobolev and Hardy’s Inequality. Fractional Laplace operator, Asymptotic behaviour of the constants and the operators as s → 0+ and s → 1−, Study of the Dirichlet problem for
Partial differential equations involving Fractional Laplace operator.
References
- Di Nezza, Eleonora; Palatucci, Giampiero; Valdinoci, Enrico Hitchhiker’sguide to the fractional Sobolev spaces. Bull. Sci. Math. 136 (2012), no. 5, 521–573.
- Felsinger, Matthieu; Kassmann, Moritz; Voigt, Paul, The Dirichlet problem for nonlocal operators. Math. Z. 279 (2015), no. 3-4, 779–809.
- Lions, J.-L. Magenes, E.: Non-homogeneous boundary value problems andapplications. Vol. I, volume 181 of Die Grundlehren der mathematischen Wissenschaften. Springer-Verlag, New York (1972).
|
Syllabus:
|
Pre-requisite(s): Instructor's Consent
Few Elements of Sobolev Spaces and Variational formulations, Besov spaces, Multi-scale Approximation and Multi-resolution, Elliptic Boundary Value Problems, Multi-resolution Galerkin Methods, Wavelets, Wavelet Galerkin Method, Adaptive Wavelet Methods, Wavelets on General Domains, Some Applications.
|
|
Credits:
|
9
|
Credits
3-0-0-0 (9)
Prerequisites
MTH309 or equivalent, MTH431A or equivalent. Familiarity with Bayesian Analysis is preferred (MTH535A or equivalent), and consent of instructor.
Objectives
The course will provide a theoretical foundation for constructing and studying Markov chain Monte Carlo (MCMC) algorithms, along with tools for analyzing MCMC output. Special focus will be given on rates of convergence of a Markov chain and comparing different MCMC algorithms. The course will primarily focus on discrete-time Markov chains on general state spaces. The objective is to equip students with the tools to develop, study, and implement an MCMC algorithm for any given problem.
Syllabus
This course presents the theoretical and practical challenges of implementing a discrete-time general state space Markov chain Monte Carlo algorithm. Metropolis-Hastings, Gibbs samplers, and other component-wise algorithms are discussed in detail. The theoretical part of the course focuses on studying rates of convergence of Markov chains, and establishing the existence of a Markov chain central limit theorem. The practical challenges of implementing these algorithms, such as step-sizes, stopping criterion, output analysis, and implementation in statistical software are also discussed in detail.
References
- Meyn, Sean P., and Richard L. Tweedie. Markov chains and stochasticstability. Springer Science and Business Media, 2012.
- Nummelin, Esa. General irreducible Markov chains and non-negative operators. Vol. 83. Cambridge University Press, 2004.
- Brooks, Steve, Andrew Gelman, Galin Jones, and Xiao-Li Meng, eds.Handbook of Markov chain Monte Carlo. CRC press, 2011.
- Lindvall, Torgny. Lectures on the coupling method. Courier Corporation,2002.
- Roberts, Gareth O., and Jeffrey S. Rosenthal. ”General state space Markovchains and MCMC algorithms.” Probability surveys 1 (2004): 20-71.
- Jones, Galin L. ”On the Markov chain central limit theorem.” Probabilitysurveys 1, no. 299-320 (2004): 5-1.
- Glynn, Peter W., and Ward Whitt. ”The asymptotic validity of sequentialstopping rules for stochastic simulations.” The Annals of Applied Probability 2, no. 1 (1992): 180-198.
- Roberts, Gareth O., and Jeffrey S. Rosenthal. ”Optimal scaling for variousMetropolisHastings algorithms.” Statistical Science16, no. 4 (2001): 351367.
- Jarner, Søren Fiig, and Ernst Hansen. ”Geometric ergodicity of Metropolis algorithms.” Stochastic Processes and their Applications 85, no. 2 (2000): 341-361.
|
Syllabus:
|
Pre-requisite: Instructor's Consent
Approximation of functions, Numerical quadrature, Methods of numerical linear algebra, Numerical solutions of nonlinear systems and optimization, Numerical solution of ordinary and partial differential equations.
Reference materials:
-
E Isaacson and H Bishop: Analysis of Numerical Methods, Dover Publications, 1994
-
J Stoer and R Bulirsch: Introduction to Numerical Analysis, Springer-verlag, 1980.
|
|
Credits:
|
9
|
Units
3-0-0-0-[9]
Prerequisites
(i) MTH 611 (Algebra-II) (ii) MTH 612 (An introduction to commutative algebra)/consent of the instructor.
Course Description:
Algebraic Number theory is a major branch of Number Theory. This aim of this course is to serve as an introduction to the subject; covering some basic concepts and results. A number field is a finite field extension of the field of rational numbers. The basic goal will be to study various arithmetic properties of a number field via its rings of integers, prime ideals, fractional ideals and units in the ring of integers.
Course Contents
- a brief review of commutative algebra - localization, Noetherian rings andmodules, integral extensions, Dedekind domains and discrete valuation ring, Spec of a ring.
- number field, ring of integer, primes and ramifications.
- class group, finiteness of class number, Dirichlet’s unit theorem.
- global fields, local fields, valuations.
- If time permits, then following additional topics will be covered
- cyclotomic fields.
- zeta functions and L-functions, class number formula.
- adeles and ideles.
References
- Number Fields, D. Marcus, Universitext, Springer-Verlag.
- Problems in Algebraic Number Theory, E. Jody and M. Ram Murty, GTM 190, Springer-Verlag.
- Algebraic Number Theory, J.S. Milne, Course notes, available at http://www.jmilne.org.
- Algebraic Number Theory, J. Neukirch, Grundlehren der MathematischenWissenschaften 322, Springer-Verlag.
- Algebraic Number Theory, S. Lang, GTM 110, Springer-Verlag.
- A course in Arithmetic, J P Serre, GTM 7, Springer-Verlag.
- Algebraic Number Theory, R. Narasimhan et.al, TIFR Pamphlet, available at www.math.tifr.res.in/ publ/pamphlets/index.html
- Introduction to commutative algebra, M. F. Atiyah, and I. G. Macdonald,Addison-Wesley Publishing Co.
Credits
3-0-0-0(9)
Prerequisites
- Analysis – I (MTH301A),
- Topology (MTH304A),
- Several variables calculus and differential geometry (MTH305A)
Syllabus
Several variables calculus: Review of inverse function theorem and implicit function theorem.
Introduction to differential manifolds, sub-manifolds and manifolds with boundary. Smooth maps between differential manifolds, tangent space, differential of smooth maps, (local) diffeomorphism. Immersions, embeddings, regular value, level sets, submersions. Tangent and cotangent bundles, vector bundles, vector fields, integral curves. Transversality. Whitney embedding theorem. Sards theorem, Morse lemma, Morse functions. Oriented intersection Theory: degree, Lefchetz fixed point theory, the Poincare-Hopf theorem. The Euler characteristic and triangulations. Integration on manifolds.
References
- Spivak: Calculus on manifolds, Springer.
- Differential Topology, Victor Guillemin and Alan Pollack (AMS ChelseaBook Series)
- Topics in Differential Topology, Amiya Mukherjee (Hindustan Book Agency)
- Topology from the Differentiable Viewpoint, John W. Milnor (PrincetonUniversity Press)
- An Introduction to Differentiable Manifolds and Riemannian Geometry, William M. Boothby (Elsevier)
|
Syllabus:
|
Pre-requisite: MTH 201, MTH 405 / Instructor's Consent
Compact Operators, Fredholm Alternative, Fredholm Operators, The Fredholm Index and the Abstract Index, Equality of Fredholm Index and Abstract Index, Essential Spectrum, Toeplitz Operators, Fredholm Theory for Toeplitz Operators, Connectedness of the Essential Spectrum
Reference materials
-
J. Conway: A course in Functional Analysis, Springer, 2006.
-
R. Douglas: Banach Algebra Techniques in Operator Theory, Springer, 1998.
-
M. Miklavcic: Applied Functional Analysis and Partial Differential Equations, World Scientific, 1998.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: Instructor’s Consent
Overview of Riemannian Geometry: Definition of Manifolds, Diffeomorphism, Sard’s Theorem, Partition of Unity, Whitney embedding theorem, Tangent spaces and Tensor fields, Integration on Manifold, Stokes Theorem, Metric Tensor, Hodge Star Operation, Stokes theorem for Riemannian Manifold, Lie Derivative, Connection, Geodesic, Riemannian Curvature, Ricci tensor, Bianchi Identity. [10]
Sobolev Spaces in Riemannian Manifold: Definitions, Density, Imbedding Theorem, Trace Theory. [15]
Linear PDE in Riemannian Manifold: Existence theory of Poisson equation, Harmonic Forms, Hodge Decomposition, Spectral theory, Gromov’s Isoperimetric Inequality, Green’s Function of the Laplacian. [15]
Reference materials:
-
Some Nonlinear Problems in Riemannian Geometry, Thierry Aubin, SMM, Springer, 1982.
-
Sobolov Spaces in Riemannian Manifold, Emmanuel Hebey, LNM, Vol-1653, Springer
|
|
Credits:
|
9
|
|
Credits:
|
2-0-1-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Basics of ANN-(Introduction, Architecture of ANN, Learning Paradigms, Learning Rules/Processes, Activation Functions); Recall of ODEs/PDEs; Multilayer ANN Model(MANNM) for DEs –Structure of MANN, Formulation and Learning Algorithms For MANNM IVPs/BVPs/ODEsystem/HODEs; Regression based ANN Model (RBANNM) for Des; Single layer functional link ANN Model (SLFLANNM) for Des; SLFLANNM with Regression Based weights; Application to Lane-Emden Equation, Emden Fowler Equation, Duffing Oscillator Equation, Van der Pol – Duffing Oscillator Equation; Simple introduction to Deep LearningApproach; Deep Galerkin Method and Implementation; Applications of DL to PDEs
|
Credits
3-0-0-0 (9)
Objective :
The idea of this course is to give exposure to the graduate and advanced undergraduate students the concept of Gamma convergence. Gamma convergence is an useful tool for solving problems in partial differential equations, specially those which admits energy functional.
Prerequisites
Some parts from MTH 404, MTH 405, Instructor’s Judgment
Course Contents
Introduction: Motivation of the Γ-convergence with 4 important examples. ΓCongervence by numbers: Lower and upper limits, Several definitions of Γconvergence, convergence of minima, upper and lower Γ-limits, properties of Γ-limits, Γ-limits indexed by a continuous parameter. Integral Problems: Relaxation and Gamma convergence in Lp spaces. Γ-convergence and convex functional. Phase Transition problem: Phase transition as segmentation problem, Gradient theory of phase transition problem, Gradient theory from point of view of Gamma convergence. Dimension Reduction problem: Problems on thin domains, Construction of recovery sequence, Non convex vector valued problem.
References
- Braides, Γ-convergence for Beginners, vol. 22 of Oxford Lecture seriesin Mathematics and its Applications, Oxford University Press, 2002.
- Dal Maso, An Introduction to Γ-Convergence, vol. 8 of Progress in Nonlinear Differential Equations and Their Applications, Birkh¨auser Boston, 1993.
|
Syllabus:
|
Pre-requisite: MTH 424/ Instructor's Consent
Periodic composite materials (one dimensional and layered materials), Homogenization of second order el- liptic equations: periodic case, Tartar's method of oscillating test functions; Convergence of energy and correctors, Method of Two-scale convergence and convergence result, Homogenization in the non-periodic case (G-convergence and H-convergence), Optimal bounds: Hashin-Shtrikman.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: Instructor's Consent
Introduction to integral equations, degenerate kernel method, projection methods, They Nystrom method, Solving multivariable integral equations, integral equations on a smooth and piecewise smooth planar boundary, boundary integral equation in 3 dimensions.
Reference materials:
-
Kendall E. Atkinson: The numerical solution of integral equations of the second kind, Cambridge University Press.
-
Rainer Kress: Linear Integral Equations, Springer.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 424/ Instructor's Consent
Introduction to Finite Difference Method (FDM), General Theory of FDM, FDM for 1-DEquations, Explicit FDM for One‐Factor Models, Trinomial method for Barrier Options, Exponentially Fitted FDM for Barrier Options, Computational issues in Barrier and Look-back option models, FDM for One‐Factor Black‐Scholes Equation, Implicit‐Explicit Method for Jump Process in Black Scholes Equations, FDM for Multi‐Factor Instrument Pricing, Heston Model, Asian Option, Multi‐Asset option, Front fixing Method, American Option.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 649 Algebraic Topology-I (Fundamental groups, covering spaces, Homology theory), Knowledge of cohomology is desirable/ Instructor consent.
-
Week 1 CW complexes, higher homotopy groups
-
Week 2 Relative homotopy groups,properties, action of fundamental group.
-
Week 3 Long exact sequence of a pair, Whitehead Theorem.
-
Week 4 Cellular and CW approximation.
-
Week 5 Postnikov Towers, k-invariants, Whitehead towers.
-
Week 6 Freudenthal Suspension Theorem, Homotopy Excision Theorem and computations.
-
Week 7 Moore spaces and Eilenberg–MacLane space.
-
Week 8 Hurewicz Theorem.
-
Week 9 Homotopy Lifting Property, Fibrations, fiber bundles.
-
Week 10 Long Exact Sequences for fibrations, applications to spheres.
-
Week 11 Whitehead products, stable homotopy groups, ring structures.
-
Week 12 Loop spaces & Suspension, exact and co-exact Puppe sequences
-
Week 13 Relations to cohomology theory.
-
Week 14 Obstruction Theory.
Reference materials:
-
A. Hatcher: “Allen Hatcher”, Cambridge Univ Press.
-
G. W. Whitehead: “Elements of Homotopy Theory”, GTM 61, Springer 1978.
-
G. Bredon: “Geometry and Topology”, GTM 139, Springer 1993.
-
A. Dold: “Lectures in Algebraic Topology”, Classics in Mathematics, Springer 1995.
-
P. May: “A Concise Course in Algebraic Topology”, University of Chicago Press, 1999.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 424/ Instructor's Consent
Introduction to Image Processing; Mathematical Preliminaries–Direct Method in Calculus of Variation, Space of functions of Bounded Variations, Viscosity solutions of PDEs, Elements of Differential Geometry; Image Restoration‐The Energy Method, PDE‐Based Methods Smoothing & Enhancing PDEs Linear & Nonlinear Diffusion models, Classical & Curvature based morphological process; The Segmentation Problem, The Mumford and Shah Functional, Geodesic Active Contours, Level set Method; Applications from computer vision– Sequence Analysis, Image Classification etc.
|
|
Credits:
|
9
|
Credits
3-0-0-0(9)
Prerequisites
Prerequisites: Instructor’s consent.
Aims of the course
The letter K in K-theory stands for the German word “Klasse”, and the classification of various kinds of mathematical objects is the main goal of the subject by associating to them their classes in certain abelian groups. Algebraic Ktheory deals with projective modules over a ring whereas topological K-theory studies vector bundles over a topological space. A common and more general setting is that of categories with some additional structure.
The course will begin with the study of the Grothendieck group, K0, associated with rings, topological spaces, symmetric monoidal categories, and exact categories. Through Bass’ K1 and K2 constructions we will motivate higher K-theory. Quillen’s genius constructions of higher K-groups and the study of various properties will constitute the final part of the course. This final part will be covered in detail if the students are familiar with the fundamental group construction.
Syllabus
- Projective modules, vector bundles, symmetric monoidal categories, exactcategories.
- The Grothendieck group and K0 of rings.
- Topological K-theory and Swan’s theorem.
- Bass’ K1 and K2 for rings.
- Geometric realization of a category.
- Quillen’s S−1S construction and + construction.
References
- Weibel, Charles A. The K-book: An introduction to algebraic K-theory, Graduate Studies in Mathematics Vol. 145, American Mathematics Society, 2013.
- Rosenberg, Jonathan. Algebraic K-theory and its applications. Graduate Texts in Mathematics, Springer Verlag New York, 1994.
- Bass, Hyman. Algebraic K-theory. W.A.Benjamin, Inc. New York, 1968.
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
MTH403 and MTH 405 / Instructor's Consent
|
|
Course Content:
|
Functional Calculi, The Spectral Theorem; Hardy Space, the Unilateral Shift, Beurling’s Theorem; Von Neumanns Theory of Spectral Sets; The Schur Class and Spectral Domains; The Sz.-Nagy Dilation Theorem and Ando’s Dilation Theorem; The Sarason Interpolation Theorem; A Model Formula for Schur class, Lurking Isometries; The MuntzSzász Interpolation Theorem, Pick Interpolation; The Corona Problem, Carleson’s corona theorem, Leechs theorem/Toeplitz corona theorem; Operator Monotone Functions, Löwner’s Theorems, Locally Matrix Monotone Functions in d Variables; The Löwner Class in d Variables, Globally Monotone Rational Functions in Two Variables
|
Credits
3-0-0-0(9)
Prerequisites
MTH302A/MTH202A/Instructor’s consent. The axioms of ZFC, Well-ordering theorem, Ordinals, Transfinite induction and recursion, Posets and Zorn’s lemma, Cardinality and cardinals, Ultrafilters.
Syllabus
Review of cardinal arithmetic, Cardinal exponentiation, Cofinality, Non-stationary ideal and club filter, Diagonal intersection and Fodor’s lemma, Banach measure problem, Ulam’s dichotomy and real valued measurable cardinals, Suslin’s problem, Diamond principle and construction of Suslin line, Martin’s axiom and its applications to measure and category on the real line, Walks on ordinals and their characteristics, Partition relations, Some open problems.
References
- Ciesielski, Set theory for the working mathematician, Cambridge university press 2012
- Hajnal and P. Hamburger, Set Theory, Cambridge university press 1999
- Komjath and V. Totik, Problems and theorems in classical set theory,Springer 2006
- Kunen, Set Theory: An introduction to independence proofs, Elsevier1980
- Todorcevic, Walks on ordinals and their characteristics, Progress inmathematics Vol. 263, Birkhauser 2007
Credits
3-0-0-0(9)
Prerequisites
MTH302A or Instructor’s consent. Background in elementary set theory: The axioms of ZFC, wellordering theorem, ordinals, transfinite recursion, Zorn’s lemma, cardinality and cardinals. Some background in first order logic is also desirable.
Syllabus
Review of ZFC and cardinal arithmetic, Infinite combinatorics, Inner models, Absoluteness and the reflection principle, Godel’s constructible universe as a model of AC and GCH, Forcing posets and generic extensions, Definability of truth in generic extensions, Cohen forcing and the consistency of the negation of CH, Countably closed forcing and the consistency of the diamond principle, Martin’s axiom, Suslin’s hypothesis and almost disjoint forcing, Applications of forcing.
References
- K. Kunen, Set Theory: An introduction to independence proofs, Elsevier 1980
- T. Jech, Set theory: Third millennium edition, Springer-Verlag 2003
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
MTH 308, MTH430
|
|
Course Content:
|
Mathematical Preliminaries; Parametrized Differential Equations; Reduced Basis Methods; Certified Error Control; Emperical Interpolation Method; Linear Problems; Time Dependent Problems; Nonlinear Problems; Non-Coercive Problems with Examples
|
|
Syllabus:
|
Pre-requisite: MSO 201/ Instructor's Consent
Measure Preserving Transformations, examples, flows, conditional probability and basic of topological groups. Ergodic Theorems, Ergodicity and Mixing. Almost everywhere convergence. Entropy, Selected topic from the following: Recurrence and Szemeredis Theorm/ Topological Dynamics/ Ornstein Theory/ Finitary coding between Bernoulli shifts and entropy invariance.
Reference materials:
-
P. Walters: Introduction to Ergodic Theory.
-
K. E. Petersen: Ergodic Theory
-
Ya. Sinai: Introduction to Ergodic Theory
|
|
Credits:
|
9
|
Credits
3-0-0-0(9)
Prerequisites
Prerequisites: MTH201, MTH204.
Aims of the course
The Coxeter groups find applications in many areas of mathematics. Understanding these groups involves the interplay of geometry, algebra, and combinatorics. The aim of this course is to familiarize students with the general theory of Coxeter groups and their Hecke algebras. Emphasis will also be on studying the examples of finite and affine reflection groups. This course will cover many topics such as Reflection groups and their generalizations, Coxeter systems, permutation representations, reduced words, Bruhat order, KazhdanLusztig theory, Chevalley’s theorem, Poincare series, root systems, classification of finite and affine Coxeter groups.
Syllabus
- Finite reflection Groups, Reflections, roots, length function, fundamentaldomain.
- Classification of finite reflection groups.
- Affine reflection Groups.
- Coxeter Groups and their classification.
- Hecke Algebras and Kazhdan-Lusztig Polynomials.
- Polynomial invariants of finite reflection groups.
References
- Anders Bjorner & Francesco Brenti, Combinatorics of Coxeter Groups, Springer GTM, 2005.
- James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge University Press, 1990.
- Michael W. Davis, The Geometry and Topology of Coxeter Groups, Princeton University Press, 2008.
- Nicolas Bourbaki, Elements Of Mathematics: Lie Groups and Lie Algebras: Chapters 4-6, Springer 2002.
- Kenneth S. Brown, Buildings, Springer, 1996.
|
Syllabus:
|
Pre-requisite: MTH204/ Instructor's Consent
Basic definitions and examples, Irreducible representations and Maschke's theorem, Constructing new representations, Schur's lemma, Characters and orthogonality relations, Regular Representation and decomposition, Number of irreducible representations of a group. Induced representation. Character table of some known groups. Representation theory of symmetric and alternating group. Algebraic integers and Burnside's pq theorem. Frobenius reciprocity formula, Group algebra and its decomposition, Mackey's irreducibility criterion. Artin's theorem on Induced characters, Elementary subgroups and Brauer's theorem.
Reference materials:
-
J.P. Serre: Linear representations of finite groups.
-
Fulton; Harris: Representation theory: A first course.
-
S. Lang, Algebra, GTM 211, Springer-Verlag.
-
G. James and M. Liebeck, Representations and Characters of Groups, Cambridge University Press.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH611/ 612/ 613
Linear groups: Topological groups; Linear groups (e.g.,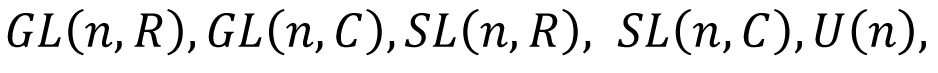 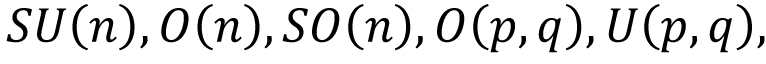 , and their topological properties (e.g., compactness, connectedness) Exponential: Exponential of a matrix, Logarithm of a matrix. Linear Lie groups: One parameter subgroups; Lie algebra of a linear Lie group; Linear Lie groups are submanifolds; Campbell-Hausdorff formula. Lie algebra: Definitions and examples; Semisimple Lie algebras; Nilpotent and solvable Lie algebras. Representations of compact groups: Unitary representations; Schur orthogonality relations; Peter-Weyl theorem; character and central functions; absolute convergence of Fourier series; Casimir operator. Haar measure: Definition; differential forms and Haar measure on linear Liegroup; Unimodular group and examples. Analysis on SU(2): Haar measure on SU(2); irreducible representations of SU(2);Laplace operator on SU(2); Fourier series on SU(2); Heat equation on SU(2). Analysis on U(n): Highest weight theorem; Weyl integration formula; Character formula; Dimension formula; Laplace operator, Fourier series and Heat equation on U(n). , and their topological properties (e.g., compactness, connectedness) Exponential: Exponential of a matrix, Logarithm of a matrix. Linear Lie groups: One parameter subgroups; Lie algebra of a linear Lie group; Linear Lie groups are submanifolds; Campbell-Hausdorff formula. Lie algebra: Definitions and examples; Semisimple Lie algebras; Nilpotent and solvable Lie algebras. Representations of compact groups: Unitary representations; Schur orthogonality relations; Peter-Weyl theorem; character and central functions; absolute convergence of Fourier series; Casimir operator. Haar measure: Definition; differential forms and Haar measure on linear Liegroup; Unimodular group and examples. Analysis on SU(2): Haar measure on SU(2); irreducible representations of SU(2);Laplace operator on SU(2); Fourier series on SU(2); Heat equation on SU(2). Analysis on U(n): Highest weight theorem; Weyl integration formula; Character formula; Dimension formula; Laplace operator, Fourier series and Heat equation on U(n).
Reference materials:
-
S C Bagchi, S Madan, A Sitaram and U B Tewari: A first course on Representation theory and Linear Lie groups, University Press.
-
Jacques Faraut: Analysis on Lie groups, Cambridge studies in advanced mathematics.
-
B. C. Hall: Lie groups, Lie algebras and Representations, Springer GTM.
-
J. Hilgert, K.-H. Neeb: Structure and Geometry of Lie groups, Springer Monograph in Mathematics.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH 405/ Instructor's Consent
Basics of Banach Algebras and C*-algebras, examples, spectrum. Commutative Banach Algebra and C*-algebras; maximal ideal spaces, Gelfand Transform; normal elements, continuous functional calculus. Representations of C*-algebras, von Neumann Algebras, WOT and SOT, density theorems, double commutant theorem. Spectral Theorem for normal operators. Abelian von Neumann algebras (Time permits: Type-I von Neumann algebras, factors, constructions of Type-II factors).
Reference materials:
-
Conway: Operator Theory.
-
Davidson: C*-algebras by examples
-
Takesaki: Operator Algebra, vol 1
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: Instructor's Consent
Introduction, Test function spaces, Calculus with distributions, supports of distributions, Structure theorems, convolutions, Fourier transforms, L1(R), L2(R) theory of Fourier Transform, Tempered distributions, Paley Wiener theorem, Wiener Tauberian theorem, Applications of distributions theory and Fourier transform to differential equations
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: MTH611/ MTH 612/ MTH 613
Definition of Lie group, Lie algebra and examples. Tangent Lie algebras Lie algebras associated to Lie groups. Correspondence between Lie algebras and simply connected Lie groups. The universal enveloping algebra of a Lie algebra and its properties. Hopf algebras and some basic Examples. Poincare-Birkhof -Witt theorem and deformations. Formal deformation of associative algebras. Formal deformation of Lie algebras. Cohomology of Lie algebras and its relation to deformation. Solvable, Nilpotent and semi-simple Lie algebras. Engel's theorem and Lie's theorem. The radical of a Lie algebra. Cartan criterion, Whitehead and Weyl theorems.
Reference materials:
-
William Fulton and Joe Harris: Representation theory, GTM-129, Springer- Verlag, New York, 1991.
-
Dimitry Fuchs: Cohomology of infinite dimensional Lie algebras. Translated from the Russian by A. B. Sosinski. Consultants Bureau, New York, 1986.
-
Susan Montgomery: Hopf algebras and their actions on rings, volume 82 of CBMS Regional Conference Series in Mathematics.
-
Frank W. Warner: Foundations of differentiable manifolds and Lie groups, GTM-94, Springer- Verlag, New York, 1983.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: None (Only for Ph.D. students of Mathematics)
Groups, Basic properties, Isomorphism theorems, Permutation groups, Sylow Theorems, Structure theorem for finite abelian groups, Rings, Integral domains, Fields, division rings, Ideals, Maximal ideals, Euclidean rings, Polynomial ring over a ring, Maximal & Prime ideals over a commutative ring with unity, Prime avoidance theorem and Chinese Remainder theorem, Field Extension, Cramer's rule, Algebraic elements and extensions, Finite fields. Determinants and their properties, Systems of linear equations, Eigenvalues and Eigenvectors, Caley Hamilton theorem, Characteristic and minimal polynomial, diagonalization, Vector spaces, Linear transformations, Inner product spaces
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: None (Only for Ph.D. students of Mathematics)
Calculus of Variations; Sturm Liouville Problem and Green's Function; Perturbation Methods and Similarity Analysis; Stability Theory.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: None (Only for Ph.D. students of Mathematics)
Metric spaces, Open and closed sets, Compactness and connectedness, Completeness, Continuous functions (several variables and on metric spaces), uniform continuity C(X), X, compact metric space, Uniform convergence, compactness criterion, Differentiation, Inverse and Implicit function theorems. Riemann Integration, Lebesgue Integration, LP spaces. Complex Analysis: Analytic functions, Harmonic conjugates, Cauchy theorems and consequences, Power series, Zeros of analytic functions, Maximum modulus theorem, Singularities, Laurent series, Residues. Mobius transformations. Hilbert spaces: Inner product, Orthogonality, Orthonormal bases, Riesz Lemma, The space L2 as a Hilbert space
|
|
Credits:
|
9
|
Credits
3-0-0-0 (9)
Prerequisites
None (Only for Ph.D. students of Statistics)
Course Contents
- Algebras and sigma algebras; Measurable spaces; Methods of introducingprobability measures on measurable space;
- Random variables; Lebesgue integral; Expectation; Conditional probabilities and conditional expectations with respect to sigma algebras;
- Radon Nikodym theorem; Inequalities of random variables; Fubini’s theorem;
- Various kinds of convergence of sequence of random variables; Convergenceof probability measures;
- Central limit theorem; delta method; Infinitely divisible and stable distributions; Zero or One laws;
- Convergence of series; Strong law of large numbers; Law of iterated logarithm; Matringales and their basic properties.
References
- L.Chung: A Course in Probability Theory, Third Edition, AcademicPress, 2001.
- R.Bhat: Modern Probability Theory, Third Edition, New Age International (P) Ltd, 2004.
- Robert B. Ash, Catherine Doleans-Dade: Probability and Measure Theory, Harcourt Academic Press, 2000.
- Lo´eve: Probability Theory-I, Graduate Text in Mathematics, FourthEdition, Springer, 1977.
- K. Basu: Measure Theory and Probability, PHI Learning Private Limited, 2012.
|
Credits:
|
3-0-0-0 (9)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Population and samples; Parametric and nonparametric models; Exponential and location scale families; Sufficiency and minimal sufficiancy; Complete statistics;Unbiased and UMVU estimation; Asymptotically unbiased estimators; Method of moments; Bayes estimators; Invariance; Minimaxity and admissibility; The method of maximum likelihood; Asymptotically efficient estimation; Variance estimation; The jacknife; The bootstrap; The NP lemma; MLR; UMP tests forone and two sided hypotheses; Unbiased and similarity; UMPU tests in exponential families; Invariance and UMPI tests; LR tests; Asymptotic tests based on likelihoods; Chisquare tests; Bayes tests; Pivotal quantities; Inverting acceptance regions of tests; The Bayesian confidence interval; Prediction sets; Length of confidence intervals; UMA and UMAU confidence sets; Invariant confidence sets.
|
|
Syllabus:
|
Pre-requisite: MTH 304, MTH 649, MTH 611/ 612/ 613
Definition of singular cohomology, axiomatic properties. Cup and cap product. Cross product and statements of Kunneth theorem and Universal coefficients theorem. Cohomology rings of projective spaces. Orientation of manifolds and Poincare duality. Definition of higher homotopy groups, homotopy exact sequence of a pair. Definition of bration, examples of brations, homotopy exact sequence of a bration, its application to computation of homotopy groups. Hurewicz homomorphism, The Hurewicz theorem. The Whitehead Theorem. Adjointness of loop and suspension, Eilenberg -Mac Lane spaces and cohomology (from Bredon).
Reference materials:
-
Hatcher: Algebraic Topology.
-
Bredon: Topology and Geometry.
-
Peter May: Concise course in Algebraic Topology.
-
Tom Dieck: Algebraic Topology.
-
Massey: Algebraic Topology: An Introduction
-
Rotman: An Introduction to Algebraic Topology
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: Instructor's Consent
Smooth Manifolds, Vector bundles, Constructing New vector bundles Out of Old. Grassmann Manifolds and Universal bundles, The classification of vector bundles. Characteristic classes for vector bundles, Stiefel Whitney classes of manifolds, Characteristic numbers of manifolds, Thom spaces and the Thom isomorphism theorem, The construction of Stiefel Whitney classes, Chern, Pontryagin, and Euler classes.
Reference materials:
-
J. P. May: A concise course in Algebraic Topology. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, IL, 1999.
-
John W. Milnor and James D. Stasheff: Characteristic classes. Annals of Mathematics Studies, No. 76. Princeton University Press, Princeton, N. J.; University of Tokyo Press, Tokyo, 1974.
|
|
Credits:
|
9
|
|
Syllabus:
|
Pre-requisite: Instructor's Consent
Newton's Method for Nonlinear Equations, Numerical Integration of ODEs, Numerical Calculation of Eigenvalues, Numerical Solution of ODE Boundary-Value problems. Discrete Time Model: Numerical Detection of Fixed Points, Periodic Orbits, Bifurcation diagrams. Continuous Time Model: Continuation of Equilibrium Curves, Numerical Detection of Bifurcation Points of Co-Dimension One and Two, Local and Global Bifurcation Diagrams. Spatio-Temporal Model: Numerical Solution of Reaction-Diffusion Equations, Travelling Waves, Turing Patterns, Coupled Map Lattice Model. Delay Differential Equations: Numerical Solution of Delayed Temporal Model and Spatio-Temporal Model.
|
|
Credits:
|
9
|
Credits
3-0-0-0 (9)
Prerequisites
MSO201A: Probability and Statistics, consent of the instructor.
Objectives
This course will present different methods of statistical pattern recognition for multivariate data.
Syllabus
Introduction to pattern recognition supervised and unsupervised classification. Dimension reduction techniques: principal component analysis, multidimensional scaling features for maximum linear separation projection pursuit. Parametric methods for discriminant analysis: Fisher’s linear discriminant function. Linear and quadratic discriminant analysis regularized discriminant analysis. Linear and nonlinear support vector machines. Cluster analysis: hierarchical and non-hierarchical techniques classification using Gaussian mixtures. Data depth: different notions of depth, concept of multivariate median, application of depth in supervised and unsupervised classification.
References
- Pattern Classification by Richard Duda, Peter Hart and David Stork.Wiley.
- The Elements of Statistical Learning: Data Mining, Inference, and Prediction by Trevor Hastie, Robert Tibshirani, Jerome Friedman. Springer.
Prerequisite: MSO201a or consent of the instructor
Credits:
3-0-0-0 (9)
Course Content:
Reliability concepts and measures, Components and systems, Coherent systems, Cuts and Paths, Modular decomposition, Bounds on system reliability; Life distributions, Survival functions, Hazard rate, Residual life time, Mean residual life function, Common life distri butions, Proportional Hazard models; Notions of aging, Aging properties of common life distributions, closure under formation of coherent structures, Convolutions and mixture of these cases; Univariate and bivariate shock models, Notions of bivariate and multi variate and dependence; Maintenance and replacement policies, Availability of repairable systems, Optimization of system reliability with redundancy.
References:
- Statistical Theory of Reliability and Life Testing, by Richard E Barlowand Frank Proschan, Holt Reinhart and Winston, Inc.;
- Life Time Data: Statistical Models and Methods, by Jayant V Deshpandeand Sudha G Purohit, World Scientific;
- Statistical Reliability Theory, by I B Gertsbakh, Marcel Dekker, Inc., NewYork and Basel;
- Life Distributions, by Albert W Marshall and Ingram Olkin, Springer Series in Statistics.
|
Syllabus:
|
Pre-requisite: MSO 201/ Instructor's Consent
Multiple linear model, estimation of parameters under spherical and non-spherical disturbances by least squares and maximum likelihood methods, tests of hypothesis, R2 and adjusted R2. Prediction, within and outside sample predictions. Problem of structural change, tests for structural change. Use of dummy variable. Specification error analysis related to explanatory variables, inclusion and deletion of explanatory variables. Idea of Stein rule estimation. Exact and stochastic linear restrictions, restricted and mixed regression analysis. Multi collinearity, problem, implications and tools for handling the problem, ridge regression. Heteroskedasticity, problem and test, estimation under Heteroskedasticity. Autocorrelation, Durbin Watson test. Errors in variables, inconsistency of least squares method, methods of consistent estimation, instrumental variable estimation. Seemingly unrelated regression equation model, least squares, generalized least squares and feasible generalized least squares estimators. Simultaneous equations model, structural and reduced forms, rank and order conditions for identifiability, indirect least squares, two stage least squares and limited information maximum likelihood methods of estimation. Additional topics like as Panel data models and unit roots & co integration.
Reference materials:
|
|
Credits:
|
9
|
|
Credits:
|
3-0-0-0 (5)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Instructor’s Preference
|
|
Credits:
|
3-0-0-0 (5)
|
|
Prerequisites:
|
Instructor’s Consent
|
|
Course Content:
|
Instructor’s Preference
|
|
|