

Abstract:

Short Biography:
Prof. Juan A. Cuesta-Albertos (Segovia, Spain, 1955) has a degree in Mathematics, specializing in Statistics and Operations Research, from the University of Valladolid, Spain. He completed his doctoral thesis at the same university, in Mathematical Sciences, under the direction of Prof. Dr. D. Miguel Martín Díaz. He taught at the Colegio Universitario de Burgos until the 1981/82 academic year, and from that moment until the present day, at the University of Cantabria, where he is a Full Professor of Statistics.
He is the author of about 85 research papers on topics such as the laws of large numbers and centralization measures in abstract spaces, bootstrap, robustness, functional data analysis, etc. Apart from continuing his research work, he has recently been paying attention to the dissemination of statistics. He was the Chief Editor of the journal TEST from 2002 to 2004, and is currently an Associate Editor of JASA. Please find more details in this link: https://personales.unican.es/cuestaj/index.html.
Abstract:

Short Biography:
Dr. Mallesham K completed his MSc in Mathematics from IIT Madras in 2011, and joined Harish-Chandra Research Institute (HRI), Allahabad, as PhD student. He received his PhD degree from HRI in September, 2018. Currently, he is a visiting scientist in the Statistics and Mathematics Unit, Indian Statistical Institute, Kolkata. His research area of interest lies in Number theory, especially in Analytic number theory.
Abstract:

Abstract:

Abstract:

Abstract:

Abstract:

Abstract:

Abstract:

Short Biography:
Dr. Ramiz Reza completed his B.Sc. from Ramakrishna Mission Vidyamandira, Belur (University of Calcutta) in 2009. After that, he obtained his Integrated Ph.D. degree (both M.S. and Ph.D.) from Indian Institute of Science, Bangalore in 2017. He started his post-doctoral research as a SERB-NPDF fellow in IISER Kolkata in September 2017. In February 2018, he moved to Chalmers University of Technology, Gothenburg, Sweden to continue his post-doctoral studies as a SERB-OPDF fellow.
Currently, he is an institute postdoctoral fellow at Indian Institute of Technology, Kanpur (since May 2019).
Abstract:

Short Biography:
Dr. Kumar completed his graduation in Mathematics from C.C.S. University Meerut in 2012, his post-graduation in Mathematics from IIT Guwahati in 2014, and Ph.D. in Mathematics from NISER, Bhubaneswar under the supervision of Dr. Anil Kumar Karn in 2020. He is currently working as an adhoc faculty in School of Sciences (Mathematics), NIT, Andhra Pradesh.
Abstract:

Short Biography:
Dr. Panda is currently a Post Doctoral Fellow at the School of Mathematical Sciences, NISER, Bhubaneswar. He obtained his B.Sc. from Gangadhar Meher Autonomous College, Sambalpur; M.Sc. from IIT Kanpur and Ph.D. from IIT Guwahati (all in Mathematics). His main research interest is algebraic combinatorics.
Abstract:

Short Biography:
Dr. Adhikari is currently a Viterbi and Zeff Post Doctoral Fellow at the Department of Electrical Engineering, Technion, Israel. Prior to that, he was a Post Doctoral Fellow at Indian Statistical Institute, Kolkata. He obtained both degrees M.S. and Ph.D. (in Mathematics) from Indian Institute of Science, Bangalore. He completed his Bachelor degree (Mathematics honours) from Ramakrishna Mission Residential College, Narendrapur (under Calcutta University).
His research interests mainly lie in probability theory and analysis, specifically, random matrix, determinantal point processes, large deviation, Steins method for normal approximation, and potential theory, free probability, stochastic geometry and random graphs.
Abstract:
such as medical imaging and geophysical imaging. First half of the talk will be a brief overview of our work related to introduced transforms and the second half will be focused on a recent work on V-line tomography for vector fields in
Abstract:

Short Biography:
Dr. Adhikari is currently a Viterbi and Zeff Post Doctoral Fellow at the Department of Electrical Engineering, Technion, Israel. Prior to that, he was a Post Doctoral Fellow at Indian Statistical Institute, Kolkata. He obtained both degrees M.S. and Ph.D. (in Mathematics) from Indian Institute of Science, Bangalore. He completed his Bachelor degree (Mathematics honours) from Ramakrishna Mission Residential College, Narendrapur (under Calcutta University). His research interests mainly lie in probability theory and analysis, specifically, random matrix, determinantal point processes, large deviation, Steins method for normal approximation, and potential theory, free probability, stochastic geometry and random graphs.
Abstract:
The aim of this talk is to prove a very important result of analysis named the Fundamental Theorem of Calculus (FTC) which basically relates the concepts of integration and differentiation. To achieve this
Short Biography:
Dr. Mishra received his PhD in 2017 under the guidance of Dr. Venky P. Krishnan from TIFR Centre for Applicable Mathematics, Bangalore, India. His primary research interests are in the field of inverse problems related to integral geometry, partial differential equations, microlocal analysis and medical imaging. Currently, he is a postdoctoral scholar in the Department of Mathematics at the University of Texas at Arlington (UTA), Texas. Before joining UTA, he was a postdoctoral scholar at the University of California, Santa Cruz from August 2017 to July 2019.
Abstract:
We have established limit theorems for the sums of dependent Bernoulli random variables. Here each successive random variable depends on previous few random variables. A previous k-sum dependent model is considered. This model is a combination of the previous all sum and the previous k-sum dependent models. The law of large numbers, the central limit theorem and the law of iterated logarithm for the sums of random variables following this model are established. A new approach using martingale differences is developed to prove these results.
Short Biography:
Currently, Dr. Singh is working at Redpine Signals India as a Research Engineer, where he is exploring the mathematical concept of Quantum Machine Learning Algorithms. He has completed his Ph.D. in Probability Theory under the supervision of Prof. Somesh Kumar in June, 2020. During his Ph.D., he also served as a Teaching Assistant for NPTEL courses for three years.
Abstract:
We have established limit theorems for the sums of dependent Bernoulli random variables. Here each successive random variable depends on previous few random variables. A previous k-sum dependent model is considered. This model is a combination of the previous all sum and the previous k-sum dependent models. The law of large numbers, the central limit theorem and the law of iterated logarithm for the sums of random variables following this model are established. A new approach using martingale differences is developed to prove these results.
Short Biography:
Currently, Dr. Singh is working at Redpine Signals India as a Research Engineer, where he is exploring the mathematical concept of Quantum Machine Learning Algorithms. He has completed his Ph.D. in Probability Theory under the supervision of Prof. Somesh Kumar in June, 2020. During his Ph.D., he also served as a Teaching Assistant for NPTEL courses for three years.
Abstract:
The aim of this talk is to prove a very important result of analysis named the Fundamental Theorem of Calculus (FTC) which basically relates the concepts of integration and differentiation. To achieve this
Short Biography:
Dr. Mishra received his PhD in 2017 under the guidance of Dr. Venky P. Krishnan from TIFR Centre for Applicable Mathematics, Bangalore, India. His primary research interests are in the field of inverse problems related to integral geometry, partial differential equations, microlocal analysis and medical imaging. Currently, he is a postdoctoral scholar in the Department of Mathematics at the University of Texas at Arlington (UTA), Texas. Before joining UTA, he was a postdoctoral scholar at the University of California, Santa Cruz from August 2017 to July 2019.
Abstract:

Short Biography:
Dr. Adhikari is currently a Viterbi and Zeff Post Doctoral Fellow at the Department of Electrical Engineering, Technion, Israel. Prior to that, he was a Post Doctoral Fellow at Indian Statistical Institute, Kolkata. He obtained both degrees M.S. and Ph.D. (in Mathematics) from Indian Institute of Science, Bangalore. He completed his Bachelor degree (Mathematics honours) from Ramakrishna Mission Residential College, Narendrapur (under Calcutta University).
His research interests mainly lie in probability theory and analysis, specifically, random matrix, determinantal point processes, large deviation, Steins method for normal approximation, and potential theory, free probability, stochastic geometry and random graphs.
Abstract:
such as medical imaging and geophysical imaging. First half of the talk will be a brief overview of our work related to introduced transforms and the second half will be focused on a recent work on V-line tomography for vector fields in
Abstract:

Short Biography:
Dr. Adhikari is currently a Viterbi and Zeff Post Doctoral Fellow at the Department of Electrical Engineering, Technion, Israel. Prior to that, he was a Post Doctoral Fellow at Indian Statistical Institute, Kolkata. He obtained both degrees M.S. and Ph.D. (in Mathematics) from Indian Institute of Science, Bangalore. He completed his Bachelor degree (Mathematics honours) from Ramakrishna Mission Residential College, Narendrapur (under Calcutta University).
His research interests mainly lie in probability theory and analysis, specifically, random matrix, determinantal point processes, large deviation, Steins method for normal approximation, and potential theory, free probability, stochastic geometry and random graphs.
Abstract:

Short Biography:
Dr. Panda is currently a Post Doctoral Fellow at the School of Mathematical Sciences, NISER, Bhubaneswar. He obtained his B.Sc. from Gangadhar Meher Autonomous College, Sambalpur; M.Sc. from IIT Kanpur and Ph.D. from IIT Guwahati (all in Mathematics). His main research interest is algebraic combinatorics.
Abstract:

Short Biography:
Dr. Kumar completed his graduation in Mathematics from C.C.S. University Meerut in 2012, his post-graduation in Mathematics from IIT Guwahati in 2014, and Ph.D. in Mathematics from NISER, Bhubaneswar under the supervision of Dr. Anil Kumar Karn in 2020. He is currently working as an adhoc faculty in School of Sciences (Mathematics), NIT, Andhra Pradesh.
Abstract:

Short Biography:
Dr. Ramiz Reza completed his B.Sc. from Ramakrishna Mission Vidyamandira, Belur (University of Calcutta) in 2009. After that, he obtained his Integrated Ph.D. degree (both M.S. and Ph.D.) from Indian Institute of Science, Bangalore in 2017. He started his post-doctoral research as a SERB-NPDF fellow in IISER Kolkata in September 2017. In February 2018, he moved to Chalmers University of Technology, Gothenburg, Sweden to continue his post-doctoral studies as a SERB-OPDF fellow.
Currently, he is an institute postdoctoral fellow at Indian Institute of Technology, Kanpur (since May 2019).
Abstract:

Abstract:

Abstract:

Abstract:

Abstract:

Abstract:

Abstract:

Short Biography:
Dr. Mallesham K completed his MSc in Mathematics from IIT Madras in 2011, and joined Harish-Chandra Research Institute (HRI), Allahabad, as PhD student. He received his PhD degree from HRI in September, 2018. Currently, he is a visiting scientist in the Statistics and Mathematics Unit, Indian Statistical Institute, Kolkata. His research area of interest lies in Number theory, especially in Analytic number theory.
Abstract:

Short Biography:
Prof. Juan A. Cuesta-Albertos (Segovia, Spain, 1955) has a degree in Mathematics, specializing in Statistics and Operations Research, from the University of Valladolid, Spain. He completed his doctoral thesis at the same university, in Mathematical Sciences, under the direction of Prof. Dr. D. Miguel Martín Díaz. He taught at the Colegio Universitario de Burgos until the 1981/82 academic year, and from that moment until the present day, at the University of Cantabria, where he is a Full Professor of Statistics.
He is the author of about 85 research papers on topics such as the laws of large numbers and centralization measures in abstract spaces, bootstrap, robustness, functional data analysis, etc. Apart from continuing his research work, he has recently been paying attention to the dissemination of statistics. He was the Chief Editor of the journal TEST from 2002 to 2004, and is currently an Associate Editor of JASA. Please find more details in this link: https://personales.unican.es/cuestaj/index.html.
Abstract:

Short Biography:
Subhabrata (Subho) Majumdar is a Senior Inventive Scientist in the Data Science and AI Research group of AT&T Labs. His research interests have two focus areas - (1) statistical machine learning - specifically predictive modelling and complex high-dimensional inference, and (2) trustworthy machine learning methods, with emphasis on human-centric qualities such as social good, robustness, fairness, privacy protection, and causality.
Subho has a PhD in Statistics from the School of Statistics, University of Minnesota under the guidance of Prof. Anshu Chatterjee. His thesis was on developing inferential methods based on statistical depth functions, focusing on robust dimension reduction and variable selection. Before joining AT&T, Subho was a postdoctoral researcher at the University of Florida Informatics Institute under Prof. George Michailidis. Subho has extensive experience in applied statistical research, with past and present collaborations spanning diverse areas like statistical chemistry, public health, behavioral genetics, and climate science. He recently co-founded the Trustworthy ML Initiative (TrustML), to bring together the community of researchers and practitioners working in that field, and lower barriers to entry for newcomers. Link to his webpage: https://shubhobm.github.io/.
Abstract:
Applications of Singular perturbation and its related boundary layer phenomena are very common in today's literature. Presence of a small parameter in the differential equation changes the behavior of the solution rapidly. Uniform meshes are inadequate for the convergence of numerical solution. The aim of the present talk is to consider the adaptive mesh generation for singularly perturbed differential equations based on moving mesh strategy. I shall start this talk with a small introduction on singular perturbation. The analytical and computational difficulties on the existed methods will be discussed. The concept of moving mesh strategy will be explained. For a posteriori based convergence analysis, a system of nonlinear singularly perturbed problems will be considered. In addition, the difference between a priori and a posteriori generated meshes and the effectivity of a posteriori mesh on the present research will be discussed. The parameter independent a priori based convergence analysis for a parabolic convection diffusion problem will be presented. In addition, an approach.
Abstract:
In this talk, definitions of different types of cross-sectional dependence and the relations between them would be discussed. We then look into parameter estimation and their asymptotic properties.
Abstract:
I will discuss on the two sections of Numerical Analysis- numerical root finding methods and interpolation techniques. I will start with the introduction on these two topics and the restriction of the popular methods. I will also discuss about interpolation and their applications.
Abstract:

Abstract:

Abstract:
In this series of two talks, we will first define long memory processes and discuss practical and theoretical examples of such processes. In addition we shall discuss the uniform reduction principle for such processes and some of its implications. This principle says that for long memory moving average processes the suitably standardized empirical process converges weakly to a degenerate Gaussian process. This is completely unlike what happens in the independent or weakly dependent case, where the suitably standardized empirical process converges weakly to Brownian bridge. In the second talk we shall discuss the problem of fitting a known d.f. or density
to the marginal error distribution of a stationary long memory moving-average process when its mean is known and unknown. When the mean is unknown and estimated by the sample mean, the first-order difference between the residual empirical and null distribution functions is asymptotically degenerate at zero. Hence, it cannot be used to fit a distribution up to an unknown mean. We show that by using a suitable class of estimators of the mean, this first order degeneracy does not occur. We also present some large sample properties of the tests based on an integrated squared-difference between kernel-type error density estimators and the expected value of the error density estimator. The asymptotic null distributions of suitably standardized test statistics are shown to be chi-square with one degree of freedom in both cases of known and unknown mean. This is totally unlike the i.i.d. errors set-up where such statistics are known to be asymptotically normally distributed.
An interested person may find the following two references helpful.
Giraitis, L., Koul, H.L. and Surgailis, D. (2012). Large sample inference for long memory processes. Imperial College Press and World Scientific.
Koul, H.L., Mimoto, N. and Surgailis, D. (2013). Goodness-of-fit tests for long memory moving average marginal density. Metrika, 76, 205-224.
Abstract:

Abstract:
In this series of two talks, we will first define long memory processes and discuss practical and theoretical examples of such processes. In addition we shall discuss the uniform reduction principle for such processes and some of its implications. This principle says that for long memory moving average processes the suitably standardized empirical process converges weakly to a degenerate Gaussian process. This is completely unlike what happens in the independent or weakly dependent case, where the suitably standardized empirical process converges weakly to Brownian bridge. In the second talk we shall discuss the problem of fitting a known d.f. or density
to the marginal error distribution of a stationary long memory moving-average process when its mean is known and unknown. When the mean is unknown and estimated by the sample mean, the first-order difference between the residual empirical and null distribution functions is asymptotically degenerate at zero. Hence, it cannot be used to fit a distribution up to an unknown mean. We show that by using a suitable class of estimators of the mean, this first order degeneracy does not occur. We also present some large sample properties of the tests based on an integrated squared-difference between kernel-type error density estimators and the expected value of the error density estimator. The asymptotic null distributions of suitably standardized test statistics are shown to be chi-square with one degree of freedom in both cases of known and unknown mean. This is totally unlike the i.i.d. errors set-up where such statistics are known to be asymptotically normally distributed.
An interested person may find the following two references helpful.
Giraitis, L., Koul, H.L. and Surgailis, D. (2012). Large sample inference for long memory processes. Imperial College Press and World Scientific.
Koul, H.L., Mimoto, N. and Surgailis, D. (2013). Goodness-of-fit tests for long memory moving average marginal density. Metrika, 76, 205-224.
Abstract:
Lie algebras are infinitesimal counterpart of Lie groups. In fact, there is a one-to-one correspondence between simply-connected Lie groups and Lie algebras (Lie III theorem).
In this talk, we will introduce 'multiplicative Poisson structures' on Lie groups (called Poisson-Lie groups) and 'Lie bialgebra' structures on Lie algebras. Finally, we show that there is a one-to-one correspondence between Poisson-Lie groups and Lie bialgebras. If time permits, I will mention some generalizations of the above correspondence.
Abstract:
While studying the dynamics of polynomial automorphisms in C2, it turns out that the class of Hénon maps, which exhibits extremely rich dynamical behaviour, is the single most important class to study. An extensive research has been done in this direction by many authors over the past thirty years. In this talk, we shall see a `rigidity' property of Hénon maps which essentially replicates a classical `rigidity' theorem of Julia sets of polynomial maps in the complex plane. In particular, we shall give an explicit description of the automorphisms in C2 which preserve the Julia sets of a given Hénon map. If time permits, we shall see a few more results regarding `rigidity' property of some special classes of automorphisms in higher dimension.
Abstract:
Natural language processing (NLP) has become a hot topic of research since the big five (GAFAM) are investing heavily into the development of this field. NLP tasks are wide-ranging, e.g. machine translation, auto completion, spam detection, argument mining, text classification, sentiment analysis, chat bots and named entity recognition. In any case, the text has to be converted somehow into numbers to use the text e.g. in classification problems.
The talk will be split into two parts. In the first part, the problem is introduced and the necessary preprocessing steps as well as simple methods for the representation of documents are described. These methods allow, e.g., to include text documents as features in modern machine learning methods used for classification and regression (supervised learning). The second part introduces the so-called neural language models which are unsupervised methods to “learn” a language. This results in embedding words and documents using so-called word or document vectors (e.g. word2vec). A disadvantage is that these vectors are not context sensitive. Therefore, we also give an outlook to the newest, usually very large, language models (based on deep learning methods) which are often freely available and can therefore be used by everybody for own purposes.
Abstract:
Current tools for multivariate density estimation struggle when the density is concentrated near a nonlinear subspace or manifold. Most approaches require choice of a kernel,with the multivariate Gaussian by far the most commonly used. Although heavy-tailed and skewed extensions have been proposed, such kernels cannot capture curvature in the support of the data. This leads to poor performance unless the sample size is very large relative to the dimension of the data. This article proposes a novel generalization of the Gaussian distribution, which includes an additional curvature parameter. We refer to the proposed class as Fisher-Gaussian (FG) kernels, since they arise by sampling from a von Mises-Fisher density on the sphere and adding Gaussian noise. The FG density has an analytic form,and is amenable to straightforward implementation within Bayesian mixture models using Markov chain Monte Carlo. We provide theory on large support, and illustrate gains relative to competitors in simulated and real data applications.
Abstract:
T11 Target structure (T11TS), a membrane glycoprotein isolated from sheep erythrocytes, reverses the immune suppressed state of brain tumor induced animals by boosting the functional status of the immune cells. This study aims at aiding in the design of more efficacious brain tumor therapies with T11 target structure. In my talk, I will discuss about the dynamics of brain-tumor immune interaction though a system of coupled non-linear ordinary differential equations. The system undergoes sensitivity analysis to identify the most sensitive parameters. In the model analysis, I obtained the criteria for the threshold level of T11TS for which the system will be tumor-free. Computer simulations were used for model verification and validation.
Abstract:
Computationally determinant and permanent of matrices are the two extreme problems. The determinant is in P whereas the permanent is a #P- complete problem, which means that the permanent cannot be computed in polynomial time unless P = NP. In this talk, we will discuss how the determinant (permanent) of a matrix can be computed in terms of the determinant (permanent) of blocks in the corresponding digraph. Under some conditions on the number of cut-vertices and block sizes the computation beats the asymptotic complexities of the state of art methods. Next, as an application of the computation of determinant using blocks, we will discuss a characterization of nonsingular block graphs which was an open problem, proposed in 2013 by Bapat and Roy.
Abstract:
Abstract:
I will discuss a discrete scattering problem which can be reduced to a 2x2 matrix factorization of Wiener-Hopf on an annulus (including the unit circle) in complex plane. An advancement made last year will be also presented that effectively solves this factorization problem but in an intricate manner. The particular factorization problem is still open from point of view of explicit factors and corresponds to an analogous problem on an infinite strip (including the real line) in complex plane (also open since several decades).
Short Biography:
Dr. Arkaprava Roy is currently a postdoctoral associate at Duke University, currently working with Dr. David Dunson. I have completed my Ph.D. in statistics in April 2018 from North Carolina State University (NCSU), under the supervision of Dr. Subhashis Ghosal and Dr. Ana-Maria Staicu after a Bachelor and Masters degree in statistics from Indian Statistical Institute, Kolkata. My focus is on data science and in developing innovative statistical modeling frameworks and corresponding inference methodology motivated by complex applications. I will be joining University of Florida, Biostatistics department in June, 2020 as an Assistant Professor.
Abstract:
Short Biography:
Dr. Ravitheja Vangala did his B.Math. from ISI Bangalore, M.Sc. in Mathematics from CMI Chennai, and Ph.D.in Mathematics from TIFR Mumbai. He works in number theory. His current research interests are reductions of local Galois representations, modular representation theory, p-adic L-functions and Iwasawa theory.
Abstract:
In 1961, James and Stein introduced an estimator of the mean of a multivariate normal distribution that achieves a smaller mean squared error than the maximum likelihood estimator in dimensions three and higher. This was in fact a surprising result by Stein. I will discuss the proof of this result. After that I will discuss some other estimators which are competitors of the James - Stein estimator and if the time permits the James-Stein estimator as an Empirical Bayes Estimator will also be discussed.
Abstract:
Abstract:
In this long talk, motivated by the need to deal with free boundary or interface problems of practical engineering applications, a variety of numerical methods will be presented. Apart from isogeometric methods (and its variants), we provide a primer to various numerical methods such as meshfree methods, cutFEM methods, and collocation methods based on Taylor series expansions. We review traditional methods and recent ones which appeared in
The last decade for a variety of applications.
Abstract:
Abstract:
In this talk, the first a posteriori error-driven adaptive finite element approach for real-time surgical simulation will be presented, and the method will be demonstrated on needle insertion problems. For simulating soft tissue deformation, the refinement strategy relies upon a hexahedron-based finite element method, combined with a posteriori error estimation driven local h-refinement. The local and global error levels in the mechanical fields (e.g., displacement or stresses) are controlled during the simulation. After showing the convergence of the algorithm on academic examples, its practical usability will be demonstrated on a percutaneous procedure involving needle insertion in a liver and brain. The brain shift phenomena is taken in to account which occurs when a craniotomy is performed. Through academic and practical examples it will be demonstrated that our adaptive approach facilitates real-time simulations. Moreover, this work provides a first step to discriminate between discretization error and modeling error by providing a robust quantification of discretization error during simulations. The proposed methodology has direct implications in increasing the accuracy, and controlling the computational expense of the simulation of percutaneous procedures such as biopsy, brachytherapy, regional anaesthesia, or cryotherapy. Moreover, the proposed approach can be helpful in the development of robotic surgeries because the simulation taking place in the control loop of a robot needs to be accurate, and to occur in real time. The talk will conclude with some discussion on future outlook towards personalised medicines.
Abstract:
In this talk, we will discuss about the boundedness of the conformal composition operators on Besov spaces defined on domains in the Euclidean plane. We will see how the regularity of domains effect the boundedness of the operators. The related open problems will also be discussed.
Abstract:
In binary classification, results from multiple diagnostic tests are often combined in many ways like logistic regression, linear discriminant analysis to improve diagnostic accuracy. In recent time, combining methods like direct maximization of the area under the ROC curve (AUC) has received significant interest among researchers in the field of medical science. In this article, we develop a combining method that maximizes a smoothing approximation of the hyper-volume under manifolds (HUM), an extended notion of AUC when disease outcomes are multi-categorical with ordinal in nature. The proposed method is distribution-free as it does not assume any distribution of the biomarkers. Consistency and asymptotic normality of the proposed method are established. The method is illustrated using simulated data sets as well as two real medical data sets.
Abstract:
Recent years have witnessed tremendous activity at the intersection of statistics, optimization and machine learning. The consequent bi-directional flow of ideas has significantly improved our understanding of the computational aspects of different statistical learning tasks. Our talk presents new results for two fundamental tasks at the intersection of statistics and optimization namely, (i) efficiently generating random samples given partial knowledge of a probability distribution, and (ii) learning parameters of an unknown distribution given samples from it. In the first part of the talk, we present non-asymptotic convergence guarantees of several popular Monte Carlo Markov Chain (MCMC) algorithms including Langevin algorithms and Hamiltonian Monte Carlo (HMC). We also underline beautiful connections between optimization and sampling, which leads to a design of faster sampling algorithms. In the second part of the talk, we present nonasymptotic results for parameter estimation of mixture models given samples from the distribution.
In particular, we provide algorithmic and statistical guarantees for the Expectation-Maximization (EM) algorithm when the number of components is incorrectly specified by the user.
Abstract:
In this talk, I shall talk about my recently finished joint work with Simeng Wang and Xumin Wang, which is the first progress on the pointwise convergence of noncommutative Fourier series, solving an open problem since Junge-Xu's remarkable ergodic maximal inequality in noncommutative analysis. Going back harmonic analysis on Euclidean space, one of our results suggests a new class of maximal inequalities which is quite interesting but challenging and deserves to be investigated.
Abstract:
Majorization is a concept from linear algebra that is used to compare disorderness in physics, computer science, economics and statistics. Recently, Gour et al (2018) extended matrix majorization to the quantum mechanical setting to accommodate ordering of quantum states.
In this talk, I will discuss a generalization of their concept of quantum majorization to the infinite dimensional setting. The entropic characterization of quantum majorization will be presented using operator space tensor products and duality . This is based on joint work with Li Gao, Satish Pandey and Sarah Plosker.
Abstract:
Let $X_1,X_2, X_3$ be Banach spaces of measurable functions in $L^p(\mathbb R)$ and let $m(\xi,\eta)$ be a locally integrable function in $\R^2$. We say that $m$ belongs to $BM(X_1,X_2,X_3)$ if \[ B_m(f,g)(x)=\int_\mathbb{R} \int_\mathbb{R} \hat{f}(\xi) \hat{g}(\eta)m(\xi,\eta)e^{2\pi i <\xi+\eta, x>}d\xi d\eta, \] defined for $f$ and $g$ with compactly supported Fourier transform, extends to a bounded bilinear operator from $X_1 \times X_2$ to $X_3$.
In this talk we investigate some properties of the class $BM(X_1,X_2,X_3)$ for general spaces which are invariant under translation, modulation and dilation, analyzing also the particular case of r.i. Banach function spaces. We shall give some examples in this class and some procedures to generate new bilinear multipliers. We shall focus in the case $m(\xi,\eta)=M(\xi-\eta)$ and find conditions for these classes to contain non zero multipliers in terms of the Boyd indices for the spaces.
Abstract:
The Vortex Filament Equation (VFE) is a model for the dynamics of a vortex _lament in a 3-D inviscid incompressible uid, and due to its geometric properties and simplicity, it has received a lot of attention recently. Given an arc-length parameterized curve X(s; _) in R3, the equation describes its evolution as
Where ^ is the usual cross product, s arc-length parameter, t time and subscripts denote the partial derivatives.
In this talk, we consider the initial datum X(s; 0) as a regular polygonal curve in the Euclidean geometry; through algebraic and numerical results, it will be shown that X(s; t) is a skew polygon at any rational time. Hence, we will see that the evolution can be related to the \Talbot e_ect" in optics. We also comment on the trajectory of one point, i.e., X(0; t) which appears to be a multifractal and resembles to the so-called Riemann's non-differentiable function.
Abstract:
This talk will provide an overview of some of the main ideas in the theory of spacings, i.e. the gaps between successive observations. After reviewing some basic properties of spacings, their use in testing statistical hypotheses and in estimating parameters will be discussed. Two-sample tests based on “spacings-frequencies” and their relationship to locally most powerful rank tests will be explored, as are some possible extensions to observations in higher dimensions.
Abstract:
This talk provides an easy introduction to the novel area of statistics, where the observations are “directions”. It is introduced by raising various scientific issues where the empirical evidence comes in the form of measuring directions, and how such measurements answer the question at hand. Such examples arise in many natural sciences like geology and biology where one may be directly measuring directions in two or three dimensions, as well as in several other seemingly unrelated and unexpected situations. New descriptive measures as well as statistical models are needed for studying such data, and the basic question one needs to answer before doing any inference in this context, is to ask if the data exhibit any preferred direction i.e. test for isotropy.
Abstract:
The theory of semihypergroups and hypergroups allows a detailed study of measure algebras that can be expressed in terms of a convolution of measures on the underlying spaces. In particular, the class of semihypergroups contains many important examples of coset and orbit spaces in locally compact groups, which do not have enough structure to be a semigroup or a hypergroup. The lack of an extensive prior research since its inception in 1972 and the signi_cant examples it contains in coset theory, orbit spaces and homogeneous spaces, opens up a number of intriguing new paths of research on semihypergroups.
In our talk, we will give a brief overview on how some well-known algebraic and analytic concepts and language of classical semigroup and group theory can be translated for semihypergroups, and investigate where the theory deviates from the classical theory of semigroups. In particular, we will discuss ideals and homomorphisms, spaces of almost periodic and weakly almost periodic functions and free-product structures in the category of semihypergroups.
Abstract:
This talk will provide a brief exposition to variable selection and sparse recovery using the L_1 penalty. Primarily, I will talk about the primal-dual witness approach and geometric insights into sparse recovery.
Abstract:
Prof. Chatterjee will discuss basic facts about high dimensional model selection in regression setup. It is currently a burning area of research in statistics. He will state and explain some recent non-asymptotic results.
Abstract:
Prof. Chatterjee will discuss basic facts about high dimensional model selection in regression setup. It is currently a burning area of research in statistics. He will state and explain some recent non-asymptotic results.
Abstract:
We consider the problem of analysis of variance, where the sample observations are random functions, and propose a test based on spatial signs. An asymptotic implementation and a bootstrap implementation of this test are developed, and their properties are investigated. We compare the performance of our test with that of several mean based tests of ANOVA for functional data in the literature, and found that Our test not only outperforms the mean based tests in several non-Gaussian models with heavy tails, but in some Gaussian models also, it exhibits better performance than the mean based tests.
Abstract:
In this talk I will give a brief introduction to G_2 geometry and gauge theory on G_2 manifolds. I will discuss the deformation theory of instantons on nearly G_2 manifolds. We will study the deformation space by identifying it as the kernel of a Dirac operator and will use this identification to specify some cases where the deformation space is trivial.
Abstract:
We shall discuss how one can estimate values of various Diophantine exponents for standard linear actions of some $2 \times 2$ matrix groups provided we have continued fraction algorithms whose denominator sizes rise exponentially. Thereafter, we illustrate this with few cases which we have been able to resolve satisfactorily. This builds upon previous works of Bugeaud, Dani, Laurent and Nogueira, among many others
The talk will be partly based on joint work with Yann Bugeaud and Zhenliang Zhang.
Abstract:
In this talk, I will first give some historical account of work on cure models. I will then describe some of the important cure rate models and then present a flexible cure rate model that encompasses some of the special cases and describe both direct maximum likelihood estimation and an efficient EM algorithm. I will then discuss some model discrimination results. Finally, I will describe some generalizations including proportional hazards model, proportional odds model, and some destructive cure models. All the models will be illustrated with some melanoma data sets.
Abstract:
A celebrated theorem of Margulis characterizes arithmetic lattices in terms of density of their commensurators. A question going back to Shalom asks the analogous question for thin subgroups. We shall report on work during the last decade or so and conclude with a recent development. In recent work with Thomas Koberda, we were able to show that for a large class of normal subgroups of rank one arithmetic lattices, the commensurator is discrete.
Abstract:
We study first passage percolation (FPP) in a Gromov-hyperbolic group G with boundary equipped with the Patterson-Sullivan measure. We associate an i.i.d. collection of random passage times to each edge of a Cayley graph of G, and investigate classical questions about asymptotics of first passage time as well as the geometry of geodesics in the FPP metric. Under suitable conditions on the passage time distribution, we show that the 'velocity' exists in almost every direction, and is almost surely constant by ergodicity of the G-action on the boundary.
For every point on the boundary, we also show almost sure coalescence of any two geodesic rays directed towards the point. Finally, we show that the variance of the first passage time grows linearly with word distance along word geodesic rays in every fixed boundary direction.
This is joint work with Riddhipratim Basu.
Abstract:
Abstract:
Warped cone is a geometric object associated with a measure preserving isometric action of a finitely generated group on a compact manifold. It encodes the geometry of the manifold, geometry of the group (Cayley graph) and the dynamics of the group. This geometric object has been introduced by J. Roe in the context of Coarse Baum-Connes conjecture (CBC conjecture). Warped cones associated with the action of amenable groups give examples of CBC conjecture and some expander graphs can be constructed from the warped cones associated with the action of Property (T) group. On the other hand, Measured Equivalence (ME) is an equivalence relation between two countable groups introduced by M. Gromov as a measure-theoretic analogue of quasi-isometry. If the ‘cocyles’ associated with a measured equivalence relation are bounded, the relation is called Uniform Measured Equivalence. In this lecture, we prove that if two warped cones are quasi-isometric, then the associated groups are Uniform Measured Equivalent. As an application, we will talk about different ME-invariants which distinguish two warped cones up to quasi-isometry. This is a work in progress.
Abstract:
I will give a brief introduction to A^1-homotopy theory and describe some applications to algebraic geometry. The presentation will be non-technical and will be based on a lot of examples.
Abstract:
Consider k ($\geq 2$) populations characterized by k probability distributions that differ only in the numerical value of a parameter (say mean). In the analysis of variance if the hypothesis of homogeneity of populations is rejected then a natural question to ask is that which of the k populations is the best population, where a population is considered to be better than the other if the numerical value of some function of the parameter associated with it is larger (or smaller) than the corresponding value for the other population. Ranking and selection problems provide a satisfactory solution to this problem. Although the ranking and selection problems have been extensively studied in the literature since 1950 there are still some unresolved problems in the area.
In this talk we will discuss one such unresolved problem and discuss a partial solution to this problem. For the ease of presentation, the problem will be discussed through the example of gamma populations.
Abstract:
The E_2-term of the Adams spectral sequence may be identified with certain derived functors, and this also holds for other Bousfield-Kan types spectral sequence.
In this talk, we'll explain how the higher terms of such spectral sequences are determined by truncations of relative derived functors, defined in terms of certain spectrally enriched functor called mapping algebras.
This is ongoing joint work with David Blanc.
Abstract:
Abstract:
Abstract:
Abstract:
Abstract:
In 1812, F. Gauss introduced classical hypergeometric series to the Royal Society of Sciences at Gotingen. Since then, this kind of special functions have been well studied by mathematicians and established many significant contributions in different branches of mathematics. In the meantime, based on an analogy between the character sum expansion of a complex valued function over finite field and the power series expansion of an analytic function, J. Greene developed an analogue for classical hypergeometric series over finite field. This function is known as Gaussian hypergeometric function. Gaussian hypergeometric functions were introduced to have a parallel study with classical hypergeometric series. However, Gaussian hypergeometric functions have certain limitations. To overcome the limitations, D. McCarthy introduced an analogue for classical hypergeometric series in the p-adic setting. In this talk, we will discuss Gauusian hypergeometric functions and hypergeometric functions in the p-adic setting. Hypergeometric functions have been applied to different areas of mathematics but the two areas of most interest to us are their relations with the traces of Hecke operators and Kloosterman sums. In the first part of the talk, we will discuss certain connections of hypergeometric functions with the traces of Hecke operators. In the 2nd part we will review Kloosterman sums and their relations with hypergeometric functions.
Abstract:
In a large variety of fluid systems, flow properties are a function of space and time, and their variation can have a dramatic effect on the flow instability. The knowledge of instability behaviour of such flow is essential for mathematical modeling, design and application of compact tools to ensure desired mechanical, optical properties and barriers of the products. Moreover, many intriguing and important fluid dynamic phenomena in nature and engineering tools are associated with complex spatio-temporal patterns (e.g. water waves, clouds, sprays, blood flow and turbulent flows in various industries etc.). The study of hydrodynamic stability is an easier way to understand the spatio-temporal behaviour of complex flow systems. This talk includes the discussion on modal linear stability analysis, analytical and numerical techniques for solving stratified multilayer problems. I will explain how the instability characteristics of bounded as well as semi-bounded viscosity-stratified flows alter effectively by scalar diffusion and boundary slip. I will also discuss the derivation of generalized Orr-Sommerfeld equation and Reynolds-Orr energy equation for stratified miscible flow with Navier-slip boundary condition.
Abstract:
We are often interested in problems in which we look for a solution y(x) of a differential equation so that y(x) satisfies a prescribed condition—that is, condition imposed on the unknown y(x) or its derivatives. In this talk, I want to discuss about the existence and uniqueness of solution for such kind of equation. I will define an initial value problem (IVP) and seek general existence theorem for real solution. I will also explain how a unique solution of the initial value problem, can be obtained by an approximation process and check the necessary/sufficient conditions for the unique solution.
Abstract:
In this talk I will give an exposition on two remarkable results of Sudipta (one jointly with P. Bandyopadhyay and the other with D. Narayana) on the geometry of subspace of finite co-dimension in space of continuous functions on a compact set K. These results which are nearly a decade old had a great impact on the study of the structure of such subspaces in other classes of Banach spaces.
Abstract:
No
Abstract:
The aim of this talk is to explain the behaviour of some conformal metrics and invariants near a smooth boundary point of a domain in the complex plane. We will be interested in the invariants associated to the Carathéodory metric such as its higher-order curvatures that were introduced by Burbea and the Hurwitz metric.
The basic technical step in all these is the method of scaling the domain near a smooth boundary point. To estimate the higher-order curvatures using scaling, we generalize an old theorem of Suita on the real analyticity of the Carathéodory metric on planar domains and in the process, we show convergence of the Szegő and Garabedian kernels as well.
We then talk about the Hurwitz metric that was introduced by D. Minda. Its construction is similar to the Kobayashi metric but the essential difference lies in the class of holomorphic maps that are considered in its definition. We show that this metric is continuous and also strengthen Minda’s theorem about its comparability with the quasi-hyperbolic metric by estimating the constants in a more natural manner.
Abstract:
In Langlands program certain invariant linear functionals on irreducible representations of algebraic groups over locally compact _elds (ex: GL2(R), GL2 (Qp)) play a central role. The simplest version of these linear functionals are called Whittaker functionals. Whittaker functionals are deeply related to invariant harmonic analysis on such groups, with arithmetic and geometry. For instance, for the group GL2, the existence of Whittaker linear functional imply the multiplicity one results in the theory of automorphic representations. The situation of multiplicity one fails for almost all other linear groups and this failure is captured by Langlands formalism of dual group. I will explain my results in the case of unitary groups in three variables.
Finally, if time permits, we shall see some weak estimates on the generalized upper and lower curvatures of the Hurwitz metric.
Abstract:
This is joint work with Marc Technau (University of Graz). We generalize a classical result by R.C. Vaughan on Diophantine approximation restricted to fractions with prime denominator to imaginary quadratic number field of class number one. Our treatment is based on Harman's sieve method in the number field setting. Moreover, we introduce a smoothing which allows us to make conveniently use of the Poisson summation formula.
Abstract:
A collective motion of cells which responds to an attractant gradient is known as “chemotaxis”. Chemotaxis-convection-diffusion is a particular type of bio convection. Due to its significant role in medical, industrial, and geophysical areas, research effort has been performed to understand the dynamics of the bacterial motility in suspension, studies through analytical, experimental, and numerical attempts previously were only for a flat free-surface of a suspension of chemotaxis bacteria in a shallow/deep chamber. We consider now a three-dimensional chemotaxis-convection-diffusion flow system with a deformed free surface. The influences of the aggregated chemotactic cells on the deformed free surface of a shallow chamber are studied analytically. The aim of our research work is to explore the nature of the instability in the system by performing a detailed linear stability analysis of steady-state oxygen and cell concentration distributions. A weakly nonlinear stability analysis has been carried out as well to determine the relative stability of the pattern formation at the onset of instability where Rayleigh number R_(α_T ) is the nonlinear control parameter of the system. The system becomes dominated by nonlinear convection terms beyond a critical R_(α_T ) , which also depends on the critical wavenumber k and Nusselt number N_(u_T ) as well as the other parameters. We have investigated the issue of how the critical R_(α_T ) in this system varies with three different sets of parameters. The Lorenz model is derived under the assumption of Bossinesq approximation. Using the method of multiscales, a Ginzburg-Landau equation is derived from the Lorenz model, the solution of which helps to quantify the energy transport through the Nusselt number N_(u_T )
Abstract:
In 1980s Goldman introduced various Lie algebra structures on the free vector space generated by the free homotopy classes of closed curves in any orientable surface F. Naturally the universal enveloping algebra and the symmetric algebra of these Lie algebras admit a Poisson algebra structure. In this talk I will define and discuss some properties of these Poisson algebras. I will explain their connections with symplectic structure of moduli space and the skein algebras of F\times [0,1] . I will also discuss how to compute center of these Poisson algebras using geometric group theory. I will mention some open problems related to these objects.
Abstract:
Differential equations have fundamental importance in engineering mathematics because many physical laws and relations can be expressed mathematically in the form of differential equations. The mathematical problems of science and engineering fields can appear as a differential equations. For example, the problem of satellite motion, current flow in an electric circuit, population growth, radioactive decay, temperature control etc. lead to differential equations. Each of the above problems are characterized by some laws which involve the rate of change of one or more quantities, with respect to the other quantities. The laws characterizing these problems when expressed mathematically, become equations involving derivatives and such equations are called differential equations. It is important to study the methods of ordinary differential equations to solve these problems. Differential equations that depends on a single variable is called as ordinary differential equations. Simplest method to be discussed are ODEs of the first order because they involve only the first derivative of the unknown function. Some first-order ODEs examples will be solved and plot their solution curve.
Abstract:
It is well known from a result of Milnor on the topology of isolated singularities that the Milnor number is a topological invariant in the complex case. We will show that the Milnor number in the real case is not a bi-Lipschitz invariant. We will produce a one-parameter deformation of a singularity which is bi-Lipschitz trivial but the Milnor number is different for two different values of the parameter variable.
Abstract:
Abstract:
Define a configuration in R^n to be a family C of finite subsets of the R^n which is closed under dilations. We say that X avoids C if no set in C is contained in X. We will discuss some problems of the following form: Given a configuration C in R^n and a subset X of R^n, can we find a "large" subset Y of X such that Y avoids C? "Y is a large subset of X" will be interpreted both measure theoretically (Y has the same Lebesgue outer measure as X) and topologically (Y is everywhere non meager in X).
Abstract:
An algorithm is a step by step procedure to solve a problem. Every algorithm has inherited parallelism in it. But all algorithms cannot be parallelized. To explore the inherited parallelism of an algorithm, few basic steps play a vital role. Interconnection network is one of such steps. Few algorithm’s performance is suited to a specific kind of interconnection network. The present talk will explore such interconnection networks and will also discuss about the problems which have better performance over which network.
Abstract:
In this talk, we discuss a semi-discrete finite difference scheme for a conservation laws driven by noise. Thanks to BV estimates, we show a compact sequence of approximate solutions, generated by the finite difference scheme, converges to the unique entropy solution of the underlying problem, as the spatial mesh size goes to zero. Moreover, we show that the expected value of the L^1 difference between the approximate solution and the unique entropy solution converges at an expected rate.
Abstract:
Several types of spatiotemporal patterns for ecological communities are ubiquitous in natural habitat such as the vegetation patterns in semiarid region and the patchy spatial distribution in plankton ecosystem. It has been believed that the generation of spatiotemporal pattern in ecological communities is a result of the combination effect of the local and external factors. There exist several external factors, such as chemical-physical limitations and environmental heterogeneity, which take part in shaping the dynamics of ecological communities. However, there exist numerous empirical evidences which suggest that one should not point at the environmental heterogeneity as sole reason behind the emergence of spatiotemporal patterns. On the other hand, studies indicate that internal factors can lead to spatiotemporal pattern formation in a completely homogeneous environment and this gives rise to the well-known theory of the self-organized pattern formation. The theoretical study on self-organized pattern formations in ecological communities has been accomplished by analyzing the reaction-diffusion systems which take into account the random movements of the concerned species. In this presentation, we will talk about a complete self-organized pattern formation scenario for a spatiotemporal prey-predator model with strong Allee effect in prey growth, Holling type-II functional response and density dependent death rate of predator. The effect of the half-saturation constant on the emergence of different types of stationary patterns and the persistence enhancing effect of the spatial component will be discussed. Also, we will present different types of invasive patterns and their implications on control and management strategies for invasive species. Further, we will discuss about the destabilizing effect of gestation delay on spatial distributions of the concerned species. Overall, a comparative study between the dynamics of spatial and corresponding non-spatial systems will be presented.1
Abstract:
Sign changes of Fourier coefficients of cusp forms are central problem in number theory and many results have been obtained in this direction. In particular, it is interesting to study the sign changes at subsequences. In this talk, we will consider the problem of sign changes of Fourier coefficients of cusp form at sum of two squares and will give a quantitative result in this direction.
Abstract:
In this talk we will describe the Safety Analysis of the Indian Oceanic Airspace project, which Indian Statistical Institute is conducting jointly with the Airports Authority of India (AAI), starting from the year 2011. The talk will concentrate on the understanding of the goal of the project, typical data structure and the current "state of the art". We will also discuss some of the statistical challenges related to such an analysis.
Abstract:
The Selmer group of an elliptic curve over a number field encodes several arithmetic data of the curve providing a p-adic approach to the Birch and Swinnerton Dyer, connecting it with the p-adic Lfunction via the Iwasawa main conjecture. Under suitable extensions of the number field, the dual Selmer becomes a module over the Iwasawa algebra of a certain compact p-adic Lie group over Z_p (the ring of padic integers), which is nothing but a completed group algebra. The structure theorem of GL(2) Iwasawa theory by Coates, Schneider and Sujatha (C-S-S) then connects the dual Selmer with the “reflexive ideals” in the Iwasawa algebra. We will give an explicit ring-theoretic presentation, by generators and relations, of such Iwasawa algebras and sketch its implications to the structure theorem of C-S-S. Furthermore, such an explicit presentation of Iwasawa algebras can be obtained for a much wider class of p-adic Lie groups viz. pro- p uniform groups and the pro-pIwahori of GL(n,Z_p). If we have time, alongside Iwasawa theoretic results, we will state results (joint with Christophe Cornut) constructing Galois representations with big image in reductive groups and thus prove the Inverse Galois problem for p-adic Lie extensions using the notion of “p-rational” number fields.
Abstract:
When examining dependence in spatial data, it can be helpful to formally assess spatial covariance structures that may not be parametrically specified or fully model-based. That is, one may wish to test for general features regarding spatial covariance without presupposing any particular, or potentially restrictive, assumptions about the joint data distribution. Current methods for testing spatial covariance are often intended for specialized inference scenarios, usually with spatial lattice data. We propose instead a general method for estimation and testing of spatial covariance structure, which is valid for a variety of inference problems (including nonparametric hypotheses) and applies to a large class of spatial sampling designs with irregular data locations. In this setting, spatial statistics have limiting distributions with complex standard errors depending on the intensity of spatial sampling, the distribution of sampling locations, and the process dependence. The proposed method has the advantage of providing valid inference in the frequency domain without estimation of such standard errors, which are often intractable, and without particular distributional assumptions about the data (e.g., Gaussianity). To illustrate, we develop the method for formally testing isotropy and separability in spatial covariance and consider confidence regions for spatial parameters in variogram model fitting. A broad result is also presented to justify the method for application to other potential problems and general scenarios with testing spatial covariance. The approach uses spatial test statistics, based on an extended version of empirical likelihood, having simple chi-square limits for calibrating tests. We demonstrate the proposed method through several numerical studies.
Abstract:
We will begin with a quick review of quantum channels and briefly present the celebrated Choi-Kraus representation theorem. These constitute the key concepts and results that are required to move forward and define a special class of quantum channels called "entanglement breaking channels" --- the quantum channels that admit a Choi-Kraus representation consisting of rank-one Choi-Kraus operators.
We then introduce the entanglement breaking rank of an entanglement breaking channel and define it to be the least number of rank-one Choi-Kraus operators required in its Choi-Kraus representation. We shall show how this rank parameter for a certain map links to an open problem in linear algebra: Zauner's conjecture. In particular, we show that the problem of computing the entanglement breaking rank of the quantum channel, that sends X in M_d to 1/(d+1) [X + Tr(X)I_d] in M_d, is equivalent to the existence problem of SIC POVM in dimension d. This is a joint work with Vern Paulsen, Jitendra Prakash, and Mizanur Rahman.
Abstract:
In this talk, we will discuss the problem whether two regression functions modelling the relation between a response and covariate in two samples differ by a shift in the horizontal and vertical axis. We consider a nonparametric situation assuming only smoothness for the regression functions. A graphical tool based on the derivatives of the regression functions and their inverses is proposed to answer this question and studied in several examples. We also formalize this question in a corresponding hypothesis and develop a statistical test. The asymptotic properties of the corresponding test statistic are investigated under the null hypothesis and under local alternatives and the finite sample properties of the new test are investigated by means of a small simulation study and real data example. This is a joint work with Holger Dette (University of Ruhr, Germany) and Weichi Wu (Tsinghua University, China).
Abstract:
In this talk, we will discuss estimation and prediction inferences for the generalized half normal and Kumaraswamy distributions under different censoring schemes. In particular we will discuss hybrid Type-I censoring, Type II progressive hybrid censoring and adaptive Type-II progressive censoring schemes. Likelihood inference and Bayesian inference will be addressed under different censoring schemes. Further we will discuss about prediction estimates and associated intervals of censored/ future observations using both frequentist and Bayesian approaches. We will numerically compare different estimations and prediction estimates. We will illustrate different methods using various real data sets. Finally we will discuss some ongoing research problem on step stress life testing model.
Abstract:
Lang, Jorgenson, and Kramer have successfully employed techniques coming from theory of heat kernel, to study and estimate various arithmetic invariants. Inspired by their ideas, we describe an approach to study estimates of cusp forms, using theory of heat kernels.
Abstract:
Let G be a connected reductive group over a finite field f of order q. When q is small, we make further assumptions on G. Then we determine precisely when G(f) admits irreducible, cuspidal representations that are self- dual, of Deligne-Lusztig type, or both. Finally, we outline some consequences for the existence of self-dual supercuspidal representations of reductive p-adic groups. This is a joint work with Jeffrey Adler.
Abstract:
Given a smooth function f : [0,1) --> \R, and scalars u_j, v_j in (0,1), I will compute the Taylor (Maclaurin) series of the function F(t) := \det A(t), where A(t) is the 2x2 matrix
f( t u_1 v_1 ) f( t u_1 v_2 )
f( t u_2 v_1 ) f( t u_2 v_2 )
C. Loewner computed the first two of these Maclaurin coefficients, in the thesis of his student R.A. Horn (Trans. AMS 1969). This was in connection with entrywise functions preserving positivity on matrices of a fixed dimension -- the case of all dimensions following from earlier work of Schur (Crelle 1911) and his student Schoenberg (Duke 1942).
It turns out that an "algebraic" family of symmetric functions is hiding inside this "analysis". We will see how this family emerges when one computes the second-order (and each subsequent higher-order) Maclaurin coefficient above. This family of functions was introduced by Cauchy (1800s) and studied by Schur in his thesis (1901). As an application, I will generalize a determinant formula named after Cauchy to arbitrary power series (over any c ommutative ring); the above is the special case f(x) = 1/(1-x) and t=1.
Abstract:
I want to explain the oldest unsolved major problem in Mathematics (called the congruent number problem). It can be traced back at least to the 10th century but it is possibly much older. It turns out to be a beautiful example of the modern theory of the arithmetic of elliptic curves, but it is more accurate to say that this theory grew out of the study of this problem.
In the 17th century, Fermat gave a wonderful proof of the first special case of this problem. It also led Fermat to his so called Last Theorem (now solved by Andrew Wiles). But the original congruent number problem remains unsolved, despite the fact that conjecturally there is a very simple and beautiful answer to it.
Abstract:
Over the last few decades, models based on fluid flow and deformation in porous media are getting a lot of attention because these models have wide range of applications in science and engineering. Specifically, Biot’s consolidation model has many applications which cover the range from geoscience to medicine. It is the aim of this talk to present the a posteriori error analysis for locking free mixed finite element method of Biot's consolidation model. We discuss three novel a posteriori error estimators and show that all three a posteriori error estimators are reliable, efficient and robust. Finally, numerical results are presented to validate the theoretical results.
Abstract:
Estimation of animal abundance and distribution over large regions remains a central challenge in statistical ecology. In our first study, we use a Bayesian smoothing technique based on a conditionally autoregressive (CAR) prior distribution and Bayesian regression to integrate data from reliable but expensive surveys conducted at smaller scales with cost-effective but less reliable data generated from surveys at wider scales to address this problem. We also investigate whether the random effects which represent the spatial association due to the CAR structure have any confounding effect on the fixed effects of the regression coefficients. Next, we develop a novel Bayesian spatially explicit capture-recapture (SECR) model that disentangles the latent ecological process of animal arrival within a detection region from the process of recording this arrival by a given set of detectors. We integrate this into an advanced version of a recent SECR model by Royle (2015) involving partially identified individuals.
The above is a joint work with Prof. Mohan Delampady.
Abstract:
This is an informal talk meant for aspiring researchers in Mathematics and related fields such as Theoretical Physics. The purpose of this talk is to convey a sense of what it takes, on a day to day basis, to succeed in research. I would like to lay bare the inner attitude of a researcher. It is based partly on my own experience, but mostly on what I have learnt while collaborating, and generally hobnobbing, with some truly great mathematicians of our times. The talk will be totally non-technical and I hope to make it very interactive.
Abstract:
The representation theory of string algebras started with the work of Gelfand and Ponomarev on Harish-Chandra representations of the Lorentz group. The methods they introduced were adapted and extended to cover the representation theory of a broad class of algebras. The term "string" algebra refers to the combinatorial description of their indecomposable finitely generated representions.
I will recall that description, and that of the morphisms between representations, outline the broad picture of the category of finitely generated modules in terms of Auslander-Reiten components and say something about the infinite-dimensional representation theory.
Abstract:
When _lms thin the viscous resistance of the con_ning surfaces controls key aspects of their dynamics. However, those surfaces do more than provide the typical boundary conditions. For example, if one of the boundaries is elastic, there are nonlocal interactions that lead to interesting and challenging mathematical problems and important applications. One unique setting occurs when the free surfaces of most solids approach the bulk melting temperature from below, and they are wet by the melt phase. Mathematically, the uid dynamics of this so-called \premelting" falls under the rubric of a class of higher-order di_usion equations governing the dynamics of viscous current down an incline, viscous gravity currents between a rigid surface and a deformable elastic sheet, wetting/dewetting, and a spate of other thin-_lm settings, to name a few. However, theunderlying forces driving the ow are uniquely associated with intermolecular forces. We discuss aclass of experimentally tested and testable premelting dynamics ows. Finally, through its inuence on the viscosity, the con_nemente_ect implicitly introduces a new universal length scale into the volume ux. Thus, there are a host of thin _lm problems, from droplet breakup to wetting/dewetting dynamics, whose properties (similarity solutions, regularization, and compact support) will changeunder the action of the con_nemente_ect. Therefore, our study suggests revisiting the mathematical structure and experimental implications of a wide range of problems within the framework of the con_nemente_ect."The game of Hex gives a constructive proof of the Brouwer's fixed point theorem”
on Feb 21, 2019 at 4:00 PM in FB 567, MATHS Dept. Seminar room
by Prof. TES Raghavanfrom University of Illinois at Chicago

Abstract:
Abstract:
Abstract:
We will discuss results concerning conjugacy-invariant norms on free groups, in particular ones that
are homogeneous and quasi-homogeneous.On values of the Riemann zeta function at odd positive integers. on January 25, 2019 at 2:30 PM in FB 567, MATHS Dept Seminar room
by Prof. Atul Dixit from Gandhinagar
Abstract:
KMS states are generalization of what is known as Gibbs state for matrices to in_nitedimen-sional
C∗-algebras. Given an inverse temperature, unlike the Gibbs state for matrix algebra,KMS states
for general in_nite dimensional C∗algebras are far from unique. We discuss how theclassical and quantum symmetry of graphs act as symmetry objects for the corresponding graphC∗algebras and the invariance of KMS states on graph C∗algebras under such symmetries. Inparticular, we shall give an example of a graph admitting in_nitely many KMS states at criticalinverse temperature all of which are invariant under classical symmetry. But interestingly, thatgraph admits unique quantum symmetry invariant KMS state.
Absract:
A topological dynamical system is a pair (X,T) where T is a homeomorphism of a compact space X. A measure preserving action is a triple (Y, \mu, S) where Y is a standard Borel space, \mu is a probability measure on X and S is a measurable automorphism of Y which preserves the measure \mu. We say that (X,T) is universal if it can embed any measure preserving action (under some suitable restrictions).
Krieger’s generator theorem shows that if X is A^Z (bi-infinite sequences in elements of A) and T is the transformation on X which shifts its elements one unit to the left then (X,T) is universal. Along with Tom Meyerovitch, we establish very general conditions under which Z^d (where now we have dcommuting transformations on X)-dynamical systems are universal.
These conditions are general enough to prove that
1) A self-homeomorphism with non-uniform specification on a compact metric space (answering a question by Quas and Soo and recovering recent results by David Burguet)
2) A generic (in the sense of dense G_\delta) self-homeomorphism of the 2-torus preserving Lebesgue measure (extending result by Lind and Thouvenot to infinite entropy)
3) Proper colourings of the Z^d lattice with more than two colours and the domino tilings of the Z^2 lattice (answering a question by Şahin and Robinson) are universal. Our results also extend to the almost Borel category giving partial answers to some questions by Gao and Jackson.
The talk will not assume background in ergodic theory and dynamical systems.
Abstract:
The standard isoperimetric inequality states that among all sets with a given fixed
volume(or area in dimension 2) the ball has the smallest perimeter. That is, written here in dimension
2, the following infimum is attained by the ball
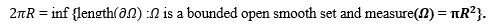
I will give an elementary overview on this inequality, such as techniques developed for theproof (symmetrization, variational method, Fourier series method in 2 dimensions), higherdimensional version, connections to partial differential equations and some generalizations. Iwill keep the talk basic, requiring no specialized knowledge in differential geometry and partial differential equations.
Abstract:
The dynamical setting of a non-autonomous system is related to the Bedford conjecture. Further,Short C^k's arises as basins of attraction of a fixed point in the non-autonomous setting. In this talk, I will discuss the relation between non-autonomous holomorphic dynamics, Short C^k's and their importance in the context of the Levi-problem. Also, I will give some construction of Short C^k's with pathological properties and finally discuss some related results and questions.
Abstract:
In multivariate linear regression, one of the major challenges is to model dependent responses from correlated predictors in a compact and interpretable manner. One promising approach is to model the coefficient matrix as a jointly sparse and low-rank matrix. Learning such a decomposition is, however, very challenging due to the simultaneous presence of orthogonality and sparsity constraints.Here, we introduce a divide and conquer strategy to infer such a coefficient matrix from data. In the divide step, we decompose the coefficient matrix into a sum of unit-rank matrices whose left and right singular vectors are sparse. In the conquer step, each unit-rank matrix is estimated either by a sequential(greedy) approach or an exclusive extraction approach. We show that the proposed algorithm is guaranteed to converge to an accumulation point and provide an efficient implementation in the R package secure. We demonstrate the efficacy of the procedure in simulation studies and two applications in genetics.
Abstract:
Over the last few decades, models based on fluid flow and deformation in porous media are getting a lot of attention because these models have wide range of applications in science and engineering. Specifically, Biot’s consolidation model has many applications which cover the range from geoscience to medicine. It is the aim of this talk to present the a posteriori error analysis for locking free mixed finite element method of Biot's consolidation model. We discuss three novel a posteriori error estimators and show that all three a posteriori error estimators are reliable, efficient and robust. Finally, numerical results are presented to validate the theoretical results.
Abstract:
The problem of estimating quantiles has received considerable attention by several researchers in the recent past from classical as well as decision theoretic point of view. It is noted that, exponential quantiles are widely used in the study of reliability, life testing and survival analysis, and related fields. Suppose there are k(≥2) normal populations with a common mean and possibly different variances. The problem of estimation of quantiles of the first population is considered with respect to a quadratic loss function. The concept of invariance is introduced to the problem. As a result, sufficient conditions are derived to improve affine and location equivariant estimators. Consequently, some complete class results have been obtained. Next, the problem of estimating ordered quantiles of two exponential distributions has been considered assuming equality on location parameters. Using order restriction on the quantiles, several new estimators have been proposed including the restricted maximum likelihood estimator. Using quadratic loss function, a sufficient condition has been obtained to improveequivariant estimators under the order restriction. Consequently, some improved estimators have been obtained. All the proposed estimators have been compared numerically. It has been seen that the percentage of risk reduction after using order restriction is quite significant.
Lack-of-fit of a parametric AR(1) model in the presence of measurement error.On January 14, 2019 at 11:00 AM in FB567, MATHS Dept Seminar room
by Prof. Hira Koul from Department of Statistics & Probability, Michigan State University
Abstract:
Recently, power law (also known as Zipf's law) has been turned out to be very natural in modelling and inferring about networks, finance, environment studies, rare events. In this seminar, Hill's estimator (best known to estimate index of regular variation) will be discussed with examples. We shall talk about the advantages and disadvantages of using Hill's estimator once population deviates from pure power law. We shall also raise some issues which are yet to be resolved.
Abstract:
We consider the limiting behaviour of the point processes associated with a branching random walk with supercritical branching mechanism and balanced regularly varying step size. Assuming that the underlying branching process satisfies Kesten-Stigum condition, it is shown that the point process sequence of properly scaled displacements coming from the n-th generation converges weakly to a Cox cluster process. This is a joint work with Rajat Subhra Hazra and Parthanil Roy.
Abstract:
We will start by defining a G_2 and a nearly G_2 structure on a seven dimensional manifold M. After surveying known results about G_2 manifolds and explaining the importance of such manifolds, we will talk about hypersurfaces of a G_2 manifold, which inherits an SU(3) structure from the ambient G_2 structure. We will give a necessary and sufficient condition for a hypersurface of a nearly G_2 manifold to be nearly Kahler.
After that, we will focus our attention on minimal hypersurfaces (zero mean curvature) and will discuss some new results in that direction.
Abstract:
Sequential multiple assignment randomized trials (SMART) are used to construct data-driven optimal treatment strategies for patients based on their treatment and covariate histories in di_erent branches of medical and behavioral sciences where a sequence of treatments are given to the patients; such sequential treatment strategies are often called dynamic treatment regimes (DTR). In the existing literature, the ma- jority of the analysis methodologies for SMART studies assume a continuous primary outcome. However, ordinal outcomes are also quite common in clinical practice; for example, the quality of life is often measured in an ordinal scale (e.g., poor, moderate, good). In this work, _rst, we develop the notion of dynamic generalized odds-ratio (dGOR) to compare two dynamic treatment regimes embedded in a 2-stage SMART with an ordinal outcome. We propose a likelihood-based approach to estimate dGOR from SMART data. Next, we discuss some combinatorial properties of dGOR and derive the asymptotic properties of its estimate. We discuss some alternative ways to estimate dGOR using concordant-discordant pairs and multi-sample U-statistic. Then, we extend the proposed methodology to a K-stage SMART. Furthermore, we propose a basic policy search algorithm that uses dGOR to _nd an optimal DTR within a _nite class. A simulation study shows the performance of the estimated dGOR in terms of the estimated power corresponding to the derived sample size. We analyze data from Sequenced Treatment Alternatives to Relieve Depression (STAR*D), a multi-stage randomized clinical trial for treating major depression, to illustrate the proposed methodology. A freely available online tool using R statistical software is provided to make the proposed methodology accessible to other researchers and practitioners.
Abstract:
Quantile regression is a more robust, comprehensive, and flexible method of statistical analysis than the commonly used mean regression methods. Quantile function completely characterizes a distribution. More and more data is getting generated in the form of multivariate, functional, and multivariate functional data and the quantile analysis gets more challenging as the data complexity increases. We propose a set of quantile analysis methods for multivariate data and multivariate functional data. In plant science, the study of salinity tolerance is crucial to improving plant growth and productivity and we apply our methods to barley field data for a salinity tolerance analysis. We apply our methods to radiosonde wind data to illustrate our proposed quantile analysis methods for visualization, outlier detection, and prediction. We model multivariate functional data for flexible quantile contour estimation and prediction.
The estimated contours are flexible in the sense that they can characterize non-Gaussian and non-convex marginal distributions. We aim to perform spatial prediction for non-Gaussian processes.
Abstract:

Abstract:
Arens irregularity of a Banach algebra is due to elements in its Banach dual which are not weakly almost periodic. The usual algebras in harmonic analysis (such as the group algebra or the Fourier algebra, when known) turned out to be all Arens irregular (even in an extreme way, as we shall see in the talk). To start, more than sixty years ago, Richard Arens himself proved that I_1 is irregular, and was followed by Mahlon Day proving the same result for many discrete groups including the abelian ones. A long exciting story followed after. The talk is an attempt to tell you the story and to explain the combinatorial reason (on the group or its dual) creating such irregularity.
Abstract:
These will be an informal talk on the use of Carleman estimates for formally determined inverse problems for hyperbolic PDEs.
Abstract: In this talk, we will discuss the existence theory of distributional solutions solving.

On a bounded domain Ω. The nonlinear structure A(x, t, Δu) is modelled after the standard parabolic p-Laplace operator. In order to do this, we develop suitable techniques to obtain a prior estimates between the solution and the boundary data. As a consequence of these estimates, a suitable compactness argument can be developed to obtain the existence result. An interesting ingredient in the proof is the careful use of the boundedness of a new type of Maximal function defined on negative Sobolev spaces. The a priori estimates proved discussed in this talk are new even for the heat equation on bounded domains.
Abstract:
Bounded sequences in the Sobolev space of non-compact manifold $M$ converge weakly in $L^p$ only after subtraction of countably many terms supported in the neighborhood of infinity. These terms are defined by functions on the manifolds-at-infinity of $M$, defined by a gluing procedure, and the sum of their respective Sobolev energies is dominated by the energy of the original sequence. Existence of minimizers in isoperimetric problems involving Sobolev norms is therefore dependent on comparison between Sobolev constants for $M$ and its manifolds-at-infinity. This is a joint work with Leszek Skrzypczak.
Abstract:
In this introductory talk, we describe an extension of the probabilistic model of diffusion that was introduced by K.Itô using his method of `stochastic differential equations'. In our model, which is based on ideas from stochastic partial differential equations, the evolving system of (solute) particles is modeled by a tempered distribution. Our method can also be viewed as an extension of the ‘method of characteristics’ in partial differential equations.
Abstract:
Since Lovasz introduced the idea of associating complexes with graphs to solve problems in Graph Theory, the properties that these complexes enjoy have been a topic of study. In this talk, I will be discussing the complexes associated with some classes of graphs, including complete graphs, Kneser and Stable Kneser graphs. The connectedness of some of the complexes associated with the graphs provide good lower bounds for the chromatic number of these graphs.
Abstract:Geometric invariant theory (GIT) provides a construction of quotients for projective algebraic varieties equipped with an action of a reductive algebraic group. Since its foundation by Mumford, GIT plays an important role in the construction of moduli (or parameter) spaces. More recently, its methods have been successfully applied to problems of representation theory, operator theory, computer vision and complexity theory. In the first part of the talk, I will give a very brief introduction to GIT and in the second part I will talk about some geometric properties of the torus and finite group quotients of Flag varieties.
Abstract:A branching random walk is a system of growing particles that starts from one particle at the origin with each particle branching and moving independently of the others after unit time. In this talk, we shall discuss how the tails of progeny and displacement distributions determine the extremal properties of branching random walks. In particular, we have been able to verify two related conjectures of Eric Brunet and Bernard Derrida in many cases that were open before.This talk is based on a joint works with Ayan Bhattacharya (PhD thesis work at Indian Statistical Institute (ISI), Kolkata, presently at Centrum Wiskunde & Informatica, Amsterdam), Rajat Subhra Hazra (ISI Kolkata), Souvik Ray (M. Stat dissertation work at ISI Kolkata, presently at Stanford University) and Philippe Soulier (University of Paris Nanterre).
Abstract:
During the last four decades, it has been realized that some problems in number theory and, in particular, in Diophantine approximation, can be solved using techniques from the theory of homogeneous dynamics. We undertake this as the theme of the talk. We shall first give a broad overview of the subject and demonstrate how some Diophantine problems can be reformulated in terms of orbit properties under certain flows in the space of lattices, following the ideas of G. A. Margulis, S. G. Dani, D. Y. Kleinbock and G. A. Margulis, E.Lindenstrauss. Subsequently, we will discuss the joint work of the speaker with Victor Beresnevich, Anish Ghosh and Sanju Velani on Inhomogeneous dual approximation on affine subspaces.
Abstract:
Randomized experiments have long been considered to be a gold standard for causal inference. The classical analysis of randomized experiments was developed under simplifying assumptions such as homogeneous treatment effects and no treatment interference leading to theoretical guarantees about the estimators of causal effects. In modern settings where experiments are commonly run on online networks (such as Facebook) or when studying naturally networked phenomena (such as vaccine efficacy) standard randomization schemes do not exhibit the same theoretical properties. To address these issues we develop a randomization scheme that is able to take into account violations of the no interference and no homophily assumptions. Under this scheme, we demonstrate the existence of unbiased estimators with bounded variance. We also provide a simplified and much more computationally tractable randomized design which leads to asymptotically consistent estimators of direct treatment effects under both dense and sparse network regimes.
Abstract:
Step-stress life testing is a popular experimental strategy, which ensures an efficient estimation of parameters from lifetime distributions in a relatively shorter period of time. In our analysis, we have used two different stress models, viz., the Cumulative Exposure and Khamis-Higgins models, with respect to the one and two-parameter exponential distributions, and the two-parameter Weibull distributions, respectively, under various censoring schemes. Both Bayesian and frequentist (wherever possible) approaches have been applied for the estimation of parameters and construction of their confidence/credible intervals. Under Bayesian analysis, estimation with order restriction on the mean lifetimes of units has been considered as well. In yet another attempt to analyze lifetime observations, we construct optimal variable acceptance sampling plans, an instrument to test the quality of manufactured items with a crucial role in the acceptance or rejection of the lot. Assuming the one-parameter exponential lifetime distribution, in presence of Type-I and Type-I hybrid censoring, we propose decision-theoretic approach based plans with a new estimator of the scale parameter. The optimal plans are obtained by minimizing the Bayes’ risk under a well-defined loss function.
Abstract:
The Cauchy dual subnormality problem asks when the Cauchy dual operator of an m-isometry is subnormal. This problem can be considered as the non-commutative analog of the fact that the reciprocal of a Bernstein function is completely monotone. We discuss this problem, its connection with a Hausdorff moment problem, its role in a problem posed by N. Salinas dating back to 1988, and some instances in which this problem can be solved. This is a joint work with A. Anand, Z. Jablonski, and J. Stochel.
Abstract:
One of the central questions in representation theory of finite groups is to describe the irreducible characters of finite groups of Lie type, namely matrix groups over finite fields. The theory of character sheaves, initiated by Lusztig, is a geometric approach to this problem. I will give a brief overview of this theory.
Abstract:
Consider a non-parametric regression model y = μ(x) + ε, where y is the response variable, x is the scalar covariate, ε is the error, and μ is the unknown non-parametric regression function. For this model, we propose a new graphical device to check whether v-th (v ≥ 1) derivative of the regression function μ is positive or not, which includes checking for monotonicity and convexity as special cases. An example is also presented that demonstrates the practical utility of the graphical device. Moreover, this graphical device is employed to formulate a class of test statistics to test the aforementioned assertion. The asymptotic distribution of the test statistics are derived, and the tests are implemented on various simulated and real data.
Abstract:
Mathematical modelling of complex ecological interactions is a central goal of research in mathematical ecology. A wide variety of mathematical models are proposed and relevant dynamical analysis is performed to understand the complex interaction among various trophic levels. Existing models are modified as well to remove their ecological discrepancies. Main objective of this talk is to provide a overview of current research trend in mathematical ecology and how dynamical complexities among interacting populations can be captured and analyzed with the help of mathematical models involving ODEs, PDEs, DDEs, SDEs and their combinations.
Abstract:
In this talk, we study the configuration of systoles (minimum length geodesics) on closed hyperbolic surfaces. The set of all systoles forms a graph on the surface, in fact a so-called fat graph, which we call the systolic graph. We study which fat graphs are systolic graphs for some surface, we call these admissible.There is a natural necessary condition on such graphs, which we call combinatorial admissibility. Our first result characterises admissibility.It follows that a sub-graph of an admissible graph is admissible. Our second major result is that there are infinitely many minimal non-admissible fat graphs (in contrast, to the classical result that there are only two minimal non-planar graphs).
Abstract:
Lag windows are commonly used in the time series, steady state simulation, and Markov chain Monte Carlo (MCMC) literature to estimate the long range variances of ergodic averages. We propose a new lugsail lag window specifically designed for improved finite sample performance. We use this lag window for batch means and spectral variance estimators in MCMC simulations to obtain strongly consistent estimators that are biased from above in finite samples and asymptotically unbiased. This quality is particularly useful when calculating effective sample size and using sequential stopping rules where they help avoid premature termination.Further, we calculate the bias and variance of lugsail estimators and demonstrate that there is little loss compared to other estimators. We also show mean square consistency of these estimators under weak conditions. Our results hold for processes that satisfy a strong invariance principle, providing a wide range of practical applications of the lag windows outside of MCMC. Finally, we study the finite sample properties of lugsail estimators in various examples.
Abstract:
Intractable integrals appear in many areas in statistics; for example, generalized linear mixed
models and Bayesian statistics. Inference in these models relies heavily on the estimation of said integrals. In this talk, I present Monte Carlo methods for estimating intractable integrals. I introduce the accept-reject sampler and demonstrate its use on an example. Although useful, the accept-reject sampler is not effective for estimating high-dimensional integrals. To this end, I present Markov Chain Monte Carlo (MCMC) methods, like the Metropolis-Hastings sampler, which allow estimation of high-dimensional integrals. I discuss important theoretical properties of MCMC methods and some statistical challenges in its practical implementation.
Abstract:
Intractable integrals appear in many areas in statistics; for example, generalized linear mixed
models and Bayesian statistics. Inference in these models relies heavily on the estimation of said integrals. In this talk, I present Monte Carlo methods for estimating intractable integrals. I introduce the accept-reject sampler and demonstrate its use on an example. Although useful, the accept-reject sampler is not effective for estimating high-dimensional integrals. To this end, I present Markov Chain Monte Carlo (MCMC) methods, like the Metropolis-Hastings sampler, which allow estimation of high-dimensional integrals. I discuss important theoretical properties of MCMC methods and some statistical challenges in its practical implementation.
Abstract:
We talk about the mod 2 cohomology ring of the Grassmannian $\widetilde{G}_{n,3}$ of oriented 3-planes in $\mathbb{R}^n$. We first state the previously known results. Then we discuss the degrees of the indecomposable elements in the cohomology ring. We have an almost complete description of the cohomology ring. This description provides lower and upper bounds on the cup length of $\widetilde{G}_{n,3}$. This talk is based on my work with Somnath Basu.
Abstract:
How can we determine whether a mean-square continuous stochastic process is finite-dimensional, and if so, what its precise dimension is? And how can we do so at a given level of confidence? This question is central to a great deal of methods for functional data, which require low-dimensional representations whether by functional PCA or other methods. The difficulty is that the determination is to be made on the basis of iid replications of the process observed discretely and with measurement error contamination. This adds a ridge to the empirical covariance, obfuscating the underlying dimension. We build a matrix-completion inspired test statistic that circumvents this issue by measuring the best possible least square fit of the empirical covariance’s off-diagonal elements, optimised over covariances of given finite rank. For a fixed grid of sufficient size, we determine the statistic’s asymptotic null distribution as the number of replications grows. We then use it to construct a bootstrap implementation of a stepwise testing procedure controlling the family-wise error rate corresponding to the collection of hypothesis formalising the question at hand. Under minimal regularity assumptions we prove that the procedure is consistent and that its bootstrap implementation is valid. The procedure involves no tuning parameters or pre-smoothing, is indifferent to the omoskedasticity or lack of it in the measurement errors, and does not assume a low-noise regime. An extensive study of the procedure’s finite-sample accuracy demonstrates remarkable performance in both real and simulated data.
This talk is based on an ongoing work with Victor Panaretos (EPFL, Switzerland).
Abstract:
Virtual element methods(VEM) is a recently developed technology considered as generalization of FEM hav- ing firm mathematical foundations, simplicity in implementation, efficiency and accuracy in computations. Unlike FEM which allows element like triangle and quadrilateral only, VEM permits very general shaped polygons including smoothed voronoi, random voronoi, distorted polygons, nonconvex elements. Basis func- tions in VEM are constructed virtually and can be computed from the informations provided by degrees of freedom(DoF) associated with the VEM space.
Moreover, basis functions are solution of some PDEs which determine the dimension of VEM space. Furthermore, we have two projection operators on VEM space; orthogonal L2projection operator Π0k,K and elliptic projection operator Π∇k,K.Both operators are definedlocally element-wish on K ∈ Th , where Th and K denote mesh partition, polygon respectively and project basis function to computable polynomial subspace sitting inside VEM space. Basically, in abstract VEMformulation, we split the bilinear form into two parts polynomial part and non-polynomial part or stabi- lization part. Polynomial part can be computed directly from degrees of freedom and non-polynomial part can be approximated from DoF ensuring same scaling as polynomial part. However, the above mentioned framework will not work in case of non-linear problems. The primary reason is that term involving nonlinearfunction e.g. (f (u)∇u • ∇v)K can not be split into polynomial and non-polynomial parts. Hence discreteform will not be computable from DoF. In view of this difficulty, we introduce a graceful idea of employingorthogonal projection operator Π0k,Kin order to discretise nonlinear term. Exploiting this technique, weencounter semi-linear parabolic and hyperbolic problems ensuring optimal order of convergence in L2 and H 1 norms. However, we assert that this technique can be employed to discretize general nonlinear type of problem.
Abstract:
Main objects of study in model theory are definable subsets of structures. For example, the definable sets in the field of complex numbers are precisely the (boolean combinations of) varieties. The (model-theoretic) Grothendieck ring of a structure aims to classify definable sets up to definable bijections. The Grothendieck ring of varieties is central to the study of motivic integration, but its computation is a wide open problem in the area. The problem of classification is simplified to a large extent if the theory of the structure admits some form of elimination of quantifiers, i.e., the complexity of the formulas describing the definable sets is in control.
In this ``double talk'', we will begin by describing the construction of the Grothendieck ring and by giving a survey of the known Grothendieck rings. Then we will present the results and techniques used to compute the Grothendieck ring in the case of dense linear orders (joint with A. Jain) and atomless boolean algebras. On our way we will also state the ``implicit function theorem’’ for boolean varieties.
Abstract:
We begin by presenting a spectral characterization theorem that settles Chevreau's problem of characterizing the class of absolutely norming operators --- operators that attain their norm on every closed subspace. We next extend the concept of absolutely norming operators to several particular (symmetric) norms and characterize these sets. In particular, we single out three (families of) norms on B(H,K): the ``Ky Fan k-norm(s)", ``the weighted Ky Fan (\pi, k)-norm(s)", and the ``(p, k)-singular norm(s)", and thereafter define and characterize the set of absolutely norming operators with respect to each of these three norms.
We then restrict our attention to the algebra B(H) of operators on a separable infinite-dimensional Hilbert space H and use the theory of symmetrically normed ideals to extend the concept of norming and absolutely norming from the usual operator norm to arbitrary symmetric norms on B(H). In addition, we exhibit the analysis of these concepts and present a constructive method to produce symmetric norm(s) on B(H) with respect to each of which the identity operator does not attain its norm.
Finally, we introduce the notion of "universally symmetric norming operators" and "universally absolutely symmetric norming operators" and characterize these classes. These refer to the operators that are, respectively, norming and absolutely norming, with respect to every symmetric norm on B(H).
In effect, we show that an operator in B(H) is universally symmetric norming if and only if it is universally absolutely symmetric norming, which in turn is possible if and only if it is compact. In particular, this result provides an alternative characterization theorem for compact operators on a separable Hilbert space.
Abstract:
In this talk, we address the question of identifying commutant and reflexivity of the multiplication d-tuple M_z on a reproducing kernel Hilbert space H of E-valued holomorphic functions on Ω, where E is a separable Hilbert space and Ω is a bounded domain in C^d admitting bounded approximation by polynomials. In case E is a finite dimensional cyclic subspace for M_z, under some natural conditions on the B(E)-valued kernel associated with H , the commutant of M_z is shown to be the algebra H^{∞}_ B(E)(Ω) of bounded holomorphic B(E)-valued functions on Ω, provided M_z satisfies the matrix-valued von Neumann’s inequality. Also, we show that a multiplication d-tuple M_z on H satisfying the von Neumann’s inequality is reflexive. The talk is based on joint work with Sameer Chavan and Shailesh Trivedi.
Abstract:
Although we can trace back the study of epidemics to the work of Daniel Bernoulli nearly two and a half centuries ago, the fact remains that key modeling advances followed the work of three individuals (two physicians) involved in the amelioration of the impact of disease at the population level a century or so ago: Sir Ronald Ross (1911) and Kermack and McKendrick (1927). Ross' interests were in the transmission dynamics and control of malaria while Kermack and McKendrick's work was directly tied in to the study of the dynamics of communicable diseases. In this presentation, I will deal primarily with the study of the dynamics of influenza type A, a communicable disease that does not present a “fixed” target. The study of the short-term dynamics of influenza, single epidemic outbreaks, makes use of extensions/modifications of the models first introduced by Kermack and McKendrick while the study of its long-term dynamics requires the introduction of modeling modifications that account for the continuous emergence of novel influenza variants: strains or subtypes. Here, I will briefly review recent work on the dynamics of influenza A/H1N1, making use of single outbreak models that account for the movement of people in the transmission process over various regions within Mexico. This research has been carried in collaboration with a large number of researchers over a couple of decades.
From a theoretical perspective, I will observe that over the past 100 years modeling epidemic processes have been based primarily on the use of the mass action law. What have we learned from this approach and what are the limitations? In this lecture, I will revisit old and “new” modeling approaches in the context of the dynamics of vector borne, sexually-transmitted and communicable diseases.
Abstract:
Let F(x; y) that belongs to Z[x; y] be a homogeneous and irreducible with degree 3. Consider F(x; y) = h for some fixed nonzero integer h. In 1909, Thue proved that this has only finitely many integral solutions. These eponymous equations have several applications. Much effort has been made to obtain upper bounds for the number of solutions of Thue equations which are independent of the size of the coefficients of F. Siegel conjectured that the number of solutions could be bounded only in terms of h and the number of non-zero coefficients of F. This was settled in the affirmative by Mueller and Schmidt. However, their bound doesn’t have the desired shape. In this talk, we present some instances when their result can be improved. This is joint work with N. Saradha.
Abstract:
Suppose p(t)=X_0+X_1t+...+X_n t^n is a polynomial where each X_i is randomly chosen to be +1 or -1. How many real roots does the polynomial have, on average? Turns out that the answer is of order \log(n). More generally, given a subset of the complex plane, how many roots are in the given subset (on average, say)? Turns out that the roots are almost all close to the unit circle, and distributed roughly uniformly in angle. We survey basic results answering these questions. The talk is aimed to be accessible to advanced undergraduate and graduate students.
Abstract:
Let F(x; y) that belongs to Z[x; y] be a homogeneous and irreducible with degree 3. Consider F(x; y) = h for some fixed nonzero integer h. In 1909, Thue proved that this has only finitely many integral solutions. These eponymous equations have several applications. Much effort has been made to obtain upper bounds for the number of solutions of Thue equations which are independent of the size of the coefficients of F. Siegel conjectured that the number of solutions could be bounded only in terms of h and the number of non-zero coefficients of F. This was settled in the affirmative by Mueller and Schmidt. However, their bound doesn’t have the desired shape. In this talk, we present some instances when their result can be improved. This is joint work with N. Saradha.
Abstract:
Penalized regression techniques are widely used in practice to perform variable selection (also known as model selection). Variable selection is important to drop the covariates from the regression model, which are irrelevant in explaining the response variable. When the number of covariates is large compared to the sample size, variable selection is indeed the most important requirement of the penalized method. Fan and Li(2001) introduced the Oracle Property as a measure of how good a penalized method is. A penalized method is said to have the oracle property provided it works as well as if the correct sub-model were known (like the Oracle who knows everything beforehand). We categorize different penalized regression methods with respect to oracle property and show that bootstrap works for each category. Moreover, we show that in most of the situations, the inference based on bootstrap is much more accurate than the oracle based inference.
Abstract:
The Adaptive Lasso (Alasso) was proposed by Zou (2006) as a modification of the Lasso for the purpose of simultaneous variable selection and estimation of the parameters in a linear regression model. Zou (2006) established that the Alasso estimator is variable-selection consistent as well as asymptotically Normal in the indices corresponding to the nonzero regression coefficients in certain fixed-dimensional settings. Minnier et al. (2011) proposed a perturbation bootstrap method and established its distributional consistency for the Alasso estimator in the fixed-dimensional setting. In this paper, however, we show that this (naive) perturbation bootstrap fails to achieve the desired second order correctness [i.e. with uniform error rate o(n^{-1/2})] in approximating the distribution of the Alasso estimator. We propose a modification to the perturbation bootstrap objective function and show that a suitably studentized version of our modified perturbation bootstrap Alasso estimator achieves second-order correctness even when the dimension of the model is allowed to grow to infinity with the sample size. As a consequence, inferences based on the modified perturbation bootstrap is more accurate than the inferences based on the oracle Normal approximation. Simulation results also justifies our method in finite samples.
Abstract:
Let g be a simple finite dimensional Lie algebra. Let A be the Laurent polynomial algebra in n + 1 commuting variables. Then g ⊗ A is naturally a Lie algebra. We now consider the universal central extension g ⊗ A ⊕ ΩA/dA. Then we add derivations of A, Der(A) and consider τ = g ⊗ A ⊕ ΩA/dA ⊕ Der(A). τ is called full toroidal Lie algebra. In this talk, we will explain the classification of irreducible integrable modules for the full toroidal Lie algebra. In the first half of the lecture, we will recall some general facts of toroidal Lie algebras and then we will go on into the technical part.
Abstract:
We briefly discuss the concept of quantum symmetry and mention how it fits into the realm of noncommutative geometry. We take a particular noncommutative topological space coming from connected, directed graph which is called graph C*-algebra and introduce a notion of quantum symmetry of such noncommutative space. A few concrete examples of such quantum symmetry will also be discussed.
Abstract:
Let Gq be the q-deformation of a simply connected simple compact Lie group G of type A, C or D and Oq(G) be the algebra of regular functions on Gq. In this talk, we show that the Gelfand-Kirillov dimension of Oq(G) is equal to the dimension of the underlying real manifold G. If time allows then we will discuss some applications of this result.
Abstract:
Cryptographic protocols base their security on the hardness of mathematical problems. Discrete Logarithm Problem (DLP) is one of them. It is known to be computationally hard in the groups of cryptographic interest. Most important among them are the multiplicative subgroup of finite fields, group of points on an elliptic curve and the group of divisor classes of degree 0 divisors (Jacobian) on a hyperelliptic curve.
Abstract:
Let g be a simple finite dimensional Lie algebra. Let A be the Laurent polynomial algebra in n + 1 commuting variables. Then g ⊗ A is naturally a Lie algebra. We now consider the universal central extension g ⊗ A ⊕ ΩA/dA. Then we add derivations of A, Der(A) and consider τ = g ⊗ A ⊕ ΩA/dA ⊕ Der(A). τ is called full toroidal Lie algebra. In this talk, we will explain the classification of irreducible integrable modules for the full toroidal Lie algebra. In the first half of the lecture, we will recall some general facts of toroidal Lie algebras and then we will go on into the technical part.
In this talk, I will discuss some of the index calculus algorithms for solving the discrete logarithm problem on these groups. More specifically, I will discuss the tower number field sieve algorithm (TNFS) for solving the discrete logarithm problem in the medium to large characteristic finite fields.
Abstract:
Multivariate two-sample testing is a very classical problem in statistics, and several methods are available for it. But, in the current era of big data and high-dimensional data, most of the existing methods fail to perform well, and they cannot even be used when the dimension of the data exceeds the sample size. In this talk, I will propose and investigate some methods based on inter-point distances, which can be conveniently used for data of arbitrary dimensions. I will discuss the merits and demerits of these methods using theoretical as well as numerical results.
Abstract:
Let F be a non-Archimedean local field F with ring of integers O and a fi nite residue fi eld k of odd characteristic. In contrast to the well-understood representation theory of the fi nite groups of Lie type GL_n(k) or of the locally compact groups GL_n(F), representations of groups GL_n(O) are considerably less understood. For example, the uniqueness of Whittaker model is well known for the complex representations of both GL_n(k) and GL_n(F) but is not known for GL_n(O).
Abstract:
In this talk we will see two possible generalizations, due to A. Connes and Frohlich et al., of the de-Rham calculus on manifolds to the noncommutative geometric context. Computations of both these will be highlighted for a class of examples provided by the quantum double suspension, which helps to compare these two generalizations in a very precise sense.
Abstract:
In this presentation, we analyze a semi-discrete finite difference scheme for a stochastic balance laws driven by multiplicative L´evy noise. By using BV estimate of approximate solutions, generated by finite difference Scheme, and Young measure technique in stochastic setting, we show that the approximate solutions converges to the unique BV entropy solution of the underlying problem. Moreover, we show that the expected value of the L^1-difference between approximate solutions and the unique entropy solution converges at a rate O(√∆x), where ∆x being a spatial mesh size.
Abstract:
We will give an overview of some techniques involved in computing the mod p reduction of p-adic Galois representations associated to certain cusp forms of GL(2).
Abstract:
We study the congruences between Galois representations and their base-change along a p-adic Lie extension. We formulate a Main conjecture arising out of these Galois representations which explains how the congruences are related to values of L-functions. This formulation requires the Galois representations to satisfy some conditions and we provide some examples where the conditions can be verified.
Abstract:
The Bellman and Isaac equations appear as the dynamic programming equations for stochastic control and differential games. This talk is concerned with the error estimates for monotone numerical approximations with the viscosity solutions of such equations. I will be focusing on both local and non-local scenario. I will discuss the most general results for equations of order less than one (non-local) and first order (local) equations. For second order equations, convex and non-convex cases (partial results!) will be treated separately. I will explain why the methods are quite different for convex and non-convex cases. To the end, I will discuss the recent developments on error estimates for non-local Isaac equations of order greater than one.
Abstract:
Transport phenomenon is of fundamental as well as practical importance in a wide spectrum of problems of different length and time scales, viz., enhanced oil recovery (EOR), carbon-capture and storage (CCS), contaminant transport in subsurface aquifers, and chromatographic separation. These transport processes in porous media feature different hydrodynamic instabilities [1, 2]. Viscous
Abstract:
This talk will present a class of tests for fitting a parametric model to the regression function in the presence of Berkson measurement error in the covariates without specifying the measurement error density but when validation data is available. The availability of validation data makes it possible to estimate the calibrated regression function non-parametrically. The proposed tests are based on a class of minimized integrated square distances between a nonparametric estimate of the calibrated regression function and the parametric null model being fitted. The asymptotic distributions of these tests under the null hypothesis and against certain alternatives are established. Surprisingly, these asymptotic distributions are the same as in the case of known measurement error density. In comparison, the asymptotic distributions of the corresponding minimum distance estimators of the null model parameters are affected by the estimation of the calibrated regression function. A simulation study shows desirable performance of a member of the proposed class of estimators and tests. This is co-authored with Pei Geng.
Abstract:
Residual empirical processes are known to play a central role in the development of statistical inference in numerous additive models. This talk will discuss some history and some recent advances in the Asymptotic uniform linearity of parametric and nonparametric residual empirical processes. We shall also discuss their usefulness in developing asymptotically distribution free goodness-of-fit tests for fitting an error distribution functions in nonparametric ARCH(1) models. Part of this talk is based on some joint work with Xiaoqing Zhu.
Abstract: Passive transport models are equations of advection-diffusion type. In most of the applications involving passive transport, the advective fields are of greater magnitude compared to molecular diffusion.
This talk attempts to present a novel theory developed by myself, Thomas Holding (Imperial) and Jeffrey Rauch (Michigan) to address these strong advection problems. Loosely speaking, our strategy is to recast the advection-diffusion equation in moving coordinates dictated by the flow associated with the advective field. Crucial to our analysis is the introduction of a fast time variable and the introduction of some new notions of weak convergence along flows in Lp spaces. We also use ideas from the theory of “homogenization structures” developed by Gabriel Nguetseng.
Our asymptotic results show the following dichotomy:
-
If the Jacobian matrix associated with the flow satisfies certain structural conditions (loosely speaking, boundedness in the fast time variable) then the strong advection limit is a non-degenerate diffusion when seen along flows.
-
On the other hand, when the Jacobian matrix associated with the flow fails to satisfy the aforementioned structural conditions, then the strong advection limit is a parabolic problem with a constraint. Here we show the appearance of an initial layer where there is an enhanced dissipation along flows.
Our results have close links to
-
the Freidlin-Wentzell theory on perturbations of dynamical systems.
-
the theory of Relaxation enhancing Lipschitz flows.
This talk will illustrate the theoretical results via various interesting examples. We address some well-known advective fields such as the Euclidean motions, the Taylor-Green cellular flows, the cat’s eye flows and some special class of the Arnold-Beltrami-Childress (ABC) flows. We will also comment on certain examples of hyperbolic or Anosov flows. Some of the results to be presented in this talk can be found in the following
Publication:T. Holding, H. Hutridurga, J. Rauch. Convergence along mean flows, SIAM J Math.
Anal., Volume 49, Issue 1, pp. 222–271 (2017).
Abstract:
In the problem of selecting a linear model to approximate the true unknown regression model, some necessary and/or sufficient conditions will be discussed for the asymptotic validity of various model selection procedures including Akaike’s AIC, Mallows’ Cp, Schwarz’ BIC, generalized AIC, etc. We shall see that these selection procedures can be classified into three distinct classes according to their asymptotic behaviour. Under some fairly weak conditions, the selection procedures in one class are asymptotically valid if there exists fixed dimensional correct models; while the selection procedures in another class are asymptotically valid if no fixed dimensional correct model exists. On the other hand, the procedures in the third class are compromises of the procedures in the first two classes.
Abstract: We consider the problem of computationally-efficient prediction from high-dimensional and highly correlated predictors in challenging settings where accurate variable selection is effectively impossible. Direct application of penalization or Bayesian methods implemented with Markov chain Monte Carlo can be computationally daunting and unstable. Hence, some type of dimensionality reduction prior to statistical analysis is in order. Common solutions include application of screening algorithms to reduce the regressors, or dimension reduction using projections of the design matrix. The former approach can be highly sensitive to threshold choice in finite samples, while the later can have poor performance in very high-dimensional settings. We propose a Targeted Random Projection (TARP) approach that combines positive aspects of both the strategies to boost performance. In particular, we propose to use information from independent screening to order the inclusion probabilities of the features in the projection matrix used for dimension reduction, leading to data-informed sparsity. Theoretical results on the predictive accuracy of TARP is discussed in detail along with the rate of computational complexity. Simulated data examples, and real data applications are given to illustrate gains relative to a variety of competitors.
Abstract:
Let G be a simple algebraic group over the field of complex numbers and B be a Borel subgroup of G. Let X_w be a Schubert variety in the flag variety G/B corresponding to an element w of the Weyl group of G, and let Z_w be the Bott–Samelson variety, a natural desingularization of X_w. In this talk we discuss the classification of the "reduced expressions of w" such that Z_w is Fano or weak Fano.
Abstract:
GATE is a big exam used for PG admissions by academic institutes as well as hiring by PSUs. In 2015, more than 8 lakh people appeared for GATE, all subjects combined.
GATE uses formula scoring with negative marking for multiple choice questions or MCQs, e.g., 1, 0, and -1/3 marks for correct, omitted, and wrong answer, respectively. Some questions have 2 marks, with -2/3 for wrong answers. Some have numerical answers, with no negative marking. The number of distinct scores possible is small (below 400), and the number of candidates is large (lakhs).
A modern statistical approach to evaluating MCQ exams uses item response theory (IRT; also called latent trait models). In this approach, each question has some parameters, called “difficulty” or “discrimination” etc., written abstractly as vector a, and each student has an ability or talent attribute, written abstractly as a scalar theta. The probability that a given question (with vector a) will be answered correctly is taken to be some specified function f(theta,a).
The definition of a, and choice of f, are modeling decisions. Later calculations, though complex, are routine. The aim is to estimate a for every question and theta for every candidate.
Two common IRT models are the Rasch model and the 2-parameter logistic (2PL) model, which I will describe. Since our question outcomes are not dichotomous (right/wrong) but polytomous (right/ omitted/wrong), we use the generalized partial credit model (GPCM), which I will describe. GPCM results are poor. The estimated abilities have low correlations with formula scores; these correlations vary across disciplines; and there are also clear conceptual problems in applying GPCM to GATE.
I will then present our new two-step IRT model, where the candidate first decides whether or not to attempt the question, and then (if attempting) gets it right or wrong. The corresponding mathematical model is simple, and aligned with how we believe GATE works. Results are better. The correlation with formula scores is higher, and near-constant across disciplines.
The policy implications of our model are positive. We now have a two-dimensional score of each candidate’s performance. The formula score represents an overall knowledge score, which may appeal to industry. The IRT ability estimate represents an academic potential estimate, which may appeal to academic institutes. If admission and hiring processes are no longer based on the same measure, both may benefit. A minor extra advantage is the possibility of awarding rationally derived ranks to individual candidates, with very few clashes.
As part of the talk, I will also discuss the estimation methods and numerical implementation. However, the emphasis will be on model statement, results, and policy implications. I hope that most of the talk will be accessible to all stakeholders in GATE.
Abstract:
Henry-Parusinski proved that the Lipschitz right classification of function germs admits continuous moduli. This allows us to introduce the notion of Lipschitz simple germs and list all such germs. We will present the method of the classification in this talk and mention some open problems.
Abstract:
In this talk, the likelihood construction is explained under different censoring schemes. Further, the techniques for estimation of the unknown parameters of the survival model are discussed under these censoring schemes.
Abstract:
In this talk, the change point problem in hazard rate is considered. The Lindley hazard change point model is discussed with its application to model bone marrow transplant data. Further, a general hazard regression change point model is discussed with exponential and Weibull distribution as special cases.
Abstract:
A {\em simplicial cell complex} K of dimension d is a poset isomorphic to the face poset of a d-dimensional simplicial CW-complex X. If a topological space M is homeomorphic to X, then K is said to be a {\em pseudotriangulation} of M. In 1974, Pezzana proved that every connected closed PL d-manifold admits a (d+1)-vertex pseudotriangulation. For such a pseudotriangulation of a PL d-manifold one can associate a (d+1)-regular colored graph, called a crystallization of the manifold.
Actually, crystallization is a graph-theoretical tool to study topological and combinatorial properties of PL manifolds. In this talk, I shall define crystallization and show some applications on PL d-Manifolds for d=2, 3 and 4.
In dimension 2, I shall show a proof of the classification of closed surfaces using crystallization. This concept has some important higher dimensional analogs, especially in dimensions 3 and 4. In dimensions 3 and 4, I shall give lower bounds for facets in a pseudotriangulation of a PL manifolds. Also, I shall talk on the regular genus (a higher dimensional analog of genus) of PL d-manifolds. Then I shall show the importance of the regular genus in dimension 4. Additivity of regular genus has been proved for a huge class of PL 4-manifolds. We have some observations on the regular genus, which is related to the 4-dimensional Smooth Poincare Conjecture.
Abstract:
Rayleigh-Bénard convection is a classical extended dissipative system which shows a plethora of bifurcations and patterns. In this talk, I'll present the results of our investigation on bifurcations and patterns near the onset of Rayleigh-Bénard convection of low-Prandtl number fluids. Investigation is done by performing direct numerical simulations (DNS) of the governing equations. Low dimensional modeling of the system using the DNS data is also done to understand the origin of different flow patterns. Our investigation reveals a rich variety of bifurcation structures involving pitchfork, Hopf, homoclinic and Neimar-Sacker bifurcations.
Abstract:
In this talk, we will discuss some recent results on the existence and uniqueness of strong solutions of certain classes of stochastic PDEs in the space of Tempered distributions. We show that these solutions can be constructed from the solutions of "related" finite dimensional stochastic differential equations driven by the same Brownian motion. We will also discuss a criterion, called the Monotonicity inequality, which implies the uniqueness of strong solutions.
Abstract:
The investigation of solute dispersion is most interesting topic of research owing to its outspread applications in various fields such as biomedical engineering, physiological fluid dynamics, etc. The aim of the present study is to know the different physiological processes involved in the solute dispersion in blood flow by assuming the relevant non-Newtonian fluid models. The axial solute dispersion process in steady/unsteady non-Newtonian fluid flow in a straight tube is analyzed in the presence and absence of absorption at the tube wall. The pulsatile nature of the blood is considered for unsteady flow. Owing to non-Newtonian nature of blood at low shear rate in small vessels, non-Newtonian Casson, Herschel-Bulkley, Carreau and Carreau-Yasuda fluid models which are most relevant for blood flow analysis are considered. The three transport coefficients i.e., exchange, convection and dispersion coefficients which describe the whole dispersion process in the system are determined. The mean concentration of solute is analyzed at all time. A comparative study of the solute dispersion is made among the Newtonian and non-Newtonian fluid models. Also, the comparison of solute dispersion between single- and two-phase models is made at all time for different radius of micro blood vessels.
Abstract:
Quasilinear symmetric and symmetrizable hyperbolic system has a wide range of applications in engineering and physics including unsteady Euler and potential equations of gas dynamics, inviscid magnetohydrodynamic (MHD) equations, shallow water equations, non-Newtonian fluid dynamics, and Einstein field equations of general relativity. In the past, the Cauchy problem of smooth solutions for these systems has been studied by several mathematicians using semigroup approach and fixed point arguments. In a recent work of M. T. Mohan and S. S. Sritharan, the local solvability of symmetric hyperbolic system is established using two different methods, viz. local monotonicity method and a frequency truncation method. The local existence and uniqueness of solutions of symmetrizable hyperbolic system is also proved by them using a frequency truncation method. Later they established the local solvability of the stochastic quasilinear symmetric hyperbolic system perturbed by Levy noise using a stochastic generalization of the localized Minty-Browder technique. Under a smallness assumption on the initial data, a global solvability for the multiplicative noise case is also proved. The essence of this talk is to give an overview of these new local solvability methods and their applications.
Abstract:
In this talk, we present the moduli problem of rank 2 torsion free Hitchin pairs of fixed Euler characteristic χ on a reducible nodal curve. We describe the moduli space of the Hitchin pairs. We define the analogue of the classical Hitchin map and describe the geometry of general Hitchin fibre. Time permits,talk on collaborated work with Balaji and Nagaraj on degeneration of moduli space of Hitchin pairs.
Abstract:
The formalism of an ``abelian category'' is meant to axiomatize the operations of linear algebra. From there, the notion of ``derived category'' as the category of complexes ``upto quasi-isomorphisms'' is natural, motivated in part by topology. The formalism of t-structures allows one to construct new abelian categories which are quite useful in practice (giving rise to new cohomology theories like intersection cohomology, for example).
In this talk we want to discuss a notion of punctual (=``point-wise'') gluing of t-structures which we formulated in the context of algebraic geometry. The essence of the construction is classical and well known, but the new language leads to several applications in the motivic world.
Abstract:
Using equivariant obstruction theory we construct equivariant maps from certain classifying spaces to representation spheres for cyclic groups, product of elementary Abelian groups and dihedral groups.
Restricting them to finite skeleta constructs equivariant maps between spaces which are related to the topological Tverberg conjecture. This answers negatively a question of \"Ozaydin posed in relation to weaker versions of the same conjecture. Further, it also has consequences for Borsuk-Ulam properties of representations of cyclic and dihedral groups.
This is joint work with Samik Basu.
Abstract:
Abstract:
Quantile regression provides a more comprehensive relationship between a response and covariates of interest compared to mean regression. When the response is subject to censoring, estimating conditional mean requires strong distributional assumptions on the error whereas (most) conditional quantiles can be estimated distribution-free. Although conceptually appealing, quantile regression for censored data is challenging due to computational and theoretical difficulties arising from non-convexity of the objective function involved. We consider a working likelihood based on Powell's objective function and place appropriate priors on the regression parameters in a Bayesian framework. In spite of the non-convexity and misspecification issues, we show that the posterior distribution is strong selection consistent. We provide a “Skinny” Gibbs algorithm that can be used to sample the posterior distribution with complexity linear in the number of variables and provide empirical evidence demonstrating the fine performance of our approach.
Abstract:
Abstract:
Given a closed smooth Riemannian manifold M, the Laplace operator is known to possess a discrete spectrum of eigenvalues going to infinity. We are interested in the properties of the nodal sets and nodal domains of corresponding eigen functions in the high energy (semiclassical) limit. We focus on some recent results on the size of nodal domains and tubular neighbourhoods of nodal sets of such high energy eigenfunctions (joint work with Bogdan Georgiev).
Abstract:
I will define affine Kac-Moody algebras, toroidal Lie algebras and full toroidal Lie algebras twisted by several finite order automorphisms and classify integrable representations of twisted full toroidal Lie algebras.
Abstract:
In recent years, one major focus of modeling spatial data has been to connect two contrasting approaches, namely, the Markov random field approach and the geostatistical approach. While the geostatistical approach allows flexible modeling of the spatial processes and can accommodate continuum spatial variation, it faces formidable computational burden for large spatial data. On the other hand, spatial Markov random fields facilitate fast statistical computations but they lack in flexibly accommodating continuum spatial variations. In this talk, I will discuss novel statistical models and methods which allow us to accommodate continuum spatial variation as well as fast matrix-free statistical computations for large spatial data. I will discuss an h-likelihood method for REML estimation and I will show that the standard errors of these estimates attain their Rao-Cramer lower bound and thus are statistically efficient. I will discuss applications on ground-water Arsenic contamination and chlorophyll concentration in ocean. This is a joint work with Debashis Mondal at Oregon State University
Abstract:
It is a well-known result from Hermann Weyl that if alpha is an irrational number in [0,1) then the number of visits of successive multiples of alpha modulo one in an interval contained in [0,1) is proportional to the size of the interval. In this talk we will revisit this problem, now looking at finer joint asymptotics of visits to several intervals with rational end points. We observe that the visit distribution can be modelled using random affine transformations; in the case when the irrational is quadratic we obtain a central limit theorem as well. Not much background in probability will be assumed. This is in joint work with Jon Aaronson and Michael Bromberg.
Abstract:
The action of Gl_n(F_q) on the polynomial ring over n variables has been studied extensively by Dickson and the invariant ring can be explicitly described. However, the action of the same group on the ring when we go modulo Frobenius powers is not completely solved. I'll talk about some interesting aspects of this modified version of the problem. More specifically, I'll discuss a conjecture by Lewis, Reiner and Stanton regarding the Hilbert series corresponding to this action and try to prove some special cases of this conjecture.
Abstract:
One way to understand representations of a group is to ‘restrict’ the representation to its various subgroups, especially to those subgroups which give multiplicity one or finite multiplicity. We shall discuss a few examples of restriction for the representations of p-adic groups. Our main examples will be the pairs $(GL_2(F), E^*) and (GL_2(E), GL_2(F))$, where $E/F$ is a quadratic extension of $p$-adic fields. These examples can be considered as low-rank cases of the well known Gross-Prasad conjectures, where one considers various ‘restrictions’ simultaneously. Further, we consider a similar ‘restriction problem’ when the groups under consideration are certain central extensions of $F$-point of a linear algebraic groups by a finite cyclic group. These are topological central extensions and called ‘covering groups’ or ‘metaplectic groups’. These covering groups are not $F$-point of any linear algebraic group. We restrict ourselves to only a two fold covers of these groups and their ‘genuine’ representations. Covering groups naturally arise in the study of modular form of half-integral weight. Some results that we will discuss are outcome of a joint work with D. Prasad.
Abstract:
Abstract:
It is a well-accepted practice in experimental situations to use auxiliary information to enhance the accuracy of the experiment i.e., to reduce the experimental error. In its simplest form of use of auxiliary information, data generated through an experiment are statistically modeled in terms of some assignable source(s) of variation, besides a chance cause of variation. The assignable causes comprise ‘treatment’ parameters and the ‘covariate’ parameter(s). This generates a family of ‘covariate models’ - serving as a ‘combination’ of ‘varietal design models’ and ‘regression models’. These are the well-known Analysis of Covariance
(ANCOVA) Models. Generally, for such models, emphasis is given on analysis of the data [in terms of inference on treatment effects contrasts] and not so much on the choice of the covariate(s) values. In this presentation, we consider the situation where there is some flexibility in the choice of the experimental units with specified values of the covariates. The notion of 'optimal' choice of values of the covariates for a given design set-up so as to minimize variance for parameter estimates has attracted attention of researchers in recent times. Hadamard matrices and Mixed orthogonal array have been conveniently used to construct optimum covariate designs with as many covariates as possible.
Abstract:
Abstract:
Recent increase in the use of 3-D magnetic resonance images (MRI) and analysis of functional magnetic resonance images (fMRI) in medical diagnostics makes imaging, especially 3-D imaging very important. Observed images often contain noise which should be removed in such a way that important image features, e.g., edges, edge structures, and other image details should be preserved, so that subsequent image analyses are reliable. Direct generalizations of existing 2-D image denoising techniques to 3-D images cannot preserve complicated edge structures well, because, the edge structures in a 3-D edge surface can be much more complicated than the edge structures in a 2-D edge curve. Moreover, the amount of smoothing should be determined locally, depending on local image features and local signal to noise ratio, which is much more challenging in 3-D images due to large number of voxels. In this talk, I will talk about a multi-resolution and locally adaptive 3-D image denoising procedure based on local clustering of the voxels. I will provide a few numerical studies which show that the denoising method can work well in many real world applications. Finally, I will talk about a few future research directions along with some introductory research problems for interested students. Most parts of my talk should be accessible to the audience of diverse academic background.
Abstract:
We shall discuss a new method of computing (integral) homotopy groups of certain manifolds in terms of the homotopy groups of spheres. The techniques used in this computation also yield formulae for homotopy groups of connected sums of sphere products and CW complexes of a similar type. In all the families of spaces considered here, we verify a conjecture of J. C.
Moore. This is joint work with Somnath Basu.
Abstract:
The theory of pseudo-differential operators provides a flexible tool for treating certain problems in linear partial differential equations. The Gohberg lemma on unit circle estimates the distance (in norm) from a given zero-order operator to the set of the compact operators from below in terms of the symbol. In this talk, I will introduce a version of the Gohberg lemma on compact Lie groups using the global calculus of pseudo-differential operators. Applying this, I will obtain the bounds for the essential spectrum and a criterion for an operator to be compact. The conditions used will be given in terms of the matrix-valued symbols of operators
Abstract:
Let $F$ be a $p$-adic field. The restriction of an irreducible admissible representation of $GL_{2}(F)$ to its maximal tori was studied by Tunnell and Saito; and they provide a very precise answer. In particular, one gets multiplicity one. This can be considered as the first case of the Gross-Prasad conjectures.
We will discuss a metaplectic variation of this question. More precisely, we will talk about the restriction of an irreducible admissible genuine representation of the two fold metaplectic cover $\widetilde{GL}_2(F)$ of $GL_2(F)$ to the inverse image in $\widetilde{GL}_2(F)$ of a maximal torus in $GL_2(F)$. We utilize a correspondence between irreducible admissible genuine supercuspidal representations of the metaplectic group widetilde{SL}_2(F)$ to irreducible admissible supercuspidal representations of linear group $SL_2(F)$. This is a joint work with D. Prasad.
Abstract:
We will describe the problem of mod p reduction of p-adic Galois representations. For two dimensional crystalline representations of the local Galois group Gal(Q¯ p |Qp ), the reduction can be computed using the compatibility of p-adic and mod p Local Langlands Correspondences; this method was first introduced by Christophe Breuil in 2003. After giving a brief sketch of the history of the problem, we will discuss how the reductions behave for representations with slopes in the half- open interval [1, 2). In the relevant cases of reducible reduction, one may also ask if the reduction is peu or tr`es ramifi´ee. We will try to sketch an answer to this question, if time permits. (Joint works with Eknath Ghate, and also with Sandra Rozensztajn for slope 1.)
Abstract:

Abstract:
Let M be a compact manifold without boundary. Define a smooth real valued function of the space of Riemannian metrics of M by taking Lp-norm of Riemannian curvature for p >= 2. Compact irreducible locally symmetric spaces are critical metrics for this functional. I will prove that rank 1 symmetric spaces are local minima for this functional by studying stability of the functional at those metrics. I will also show examples of irreducible symmetric metrics which are not local minima for it.
Abstract:
Unfolding operators have been introduced and used to study homogenization problems. Initially, it was introduced for problems with rapidly oscillating coefficients and porous domains. Later, this has been developed for domains with oscillating boundaries, typically with rectangular or pillar type boundaries which are classified as non-smooth.
In this talk, we will demonstrate the development of generalized unfolding operators, where the oscillations of the domain can be smooth and hence it has wider applications. We will also see the further adaptation of this new unfolding operators for circular domains with rapid oscillations with high amplitude of O(1). This has been applied to homogenization problems in circular domains as well.
Abstract:
We describe three approaches to the classical p-completion(or localization) of a topological space: as spaces, through cosimplicial space resolutions, and through mapping algebras – and show how they are related through appropriate "universal" systems of higher cohomology operations. All terms involved will be explained in the talk.
Abstract:
We deal with the following eigenvalue optimization problem: Given a bounded open disk $B$ in a plane, how to place an obstacle $P$ of fixed shape and size within $B$ so as to maximize or minimize the fundamental eigenvalue $lambda_1$ of the Dirichlet Laplacian on $B setmunus P$. This means that we want to extremize the function $rho \rightarrow lambda_1(B setminus rho(P))$, where $rho$ runs over the set of rigid motions such that $rho(P) subset B$. We answer this problem in the case where $P$ is invariant under the action of a dihedral group $D_{2n}$, and where the distance from the center of the obstacle $P$ to the boundary is monotonous as a function of the argument between two axes of symmetry. The extremal configurations correspond to the cases where the axes of symmetry of $P$ coincide with a diameter of $B$. The maximizing and the minimizing configurations are identified.
Abstract:
We deal with the following eigenvalue optimization problem: Given a bounded open disk B in a plane, how to place an obstacle P of fixed shape and size within B so as to maximize or minimize the fundamental eigenvalue
λ1 of the Dirichlet Laplacian on B \ P . This means that we want to extremize the function ρ → λ1 (B \ ρ(P)), where ρ runs over the set of rigid motions such that ρ(P) ⊂ B. We answer this problem in the case where P is invariant under the action of a dihedral group D 2n, and where the distance from the center of the obstacle P to the boundary is monotonous as a function of the argument between two axes of symmetry. The extremal configurations correspond to the cases where the axes of symmetry of P coincide with a diameter of B. The maximizing and the minimizing configurations are identified.
