Abstract:
In this talk, I shall talk about my recently finished joint work with Simeng Wang and Xumin Wang, which is the first progress on the pointwise convergence of noncommutative Fourier series, solving an open problem since Junge-Xu's remarkable ergodic maximal inequality in noncommutative analysis. Going back harmonic analysis on Euclidean space, one of our results suggests a new class of maximal inequalities which is quite interesting but challenging and deserves to be investigated.
Abstract:
Majorization is a concept from linear algebra that is used to compare disorderness in physics, computer science, economics and statistics. Recently, Gour et al (2018) extended matrix majorization to the quantum mechanical setting to accommodate ordering of quantum states.
In this talk, I will discuss a generalization of their concept of quantum majorization to the infinite dimensional setting. The entropic characterization of quantum majorization will be presented using operator space tensor products and duality . This is based on joint work with Li Gao, Satish Pandey and Sarah Plosker.
Abstract:
Let $X_1,X_2, X_3$ be Banach spaces of measurable functions in $L^p(\mathbb R)$ and let $m(\xi,\eta)$ be a locally integrable function in $\R^2$. We say that $m$ belongs to $BM(X_1,X_2,X_3)$ if \[ B_m(f,g)(x)=\int_\mathbb{R} \int_\mathbb{R} \hat{f}(\xi) \hat{g}(\eta)m(\xi,\eta)e^{2\pi i <\xi+\eta, x>}d\xi d\eta, \] defined for $f$ and $g$ with compactly supported Fourier transform, extends to a bounded bilinear operator from $X_1 \times X_2$ to $X_3$.
In this talk we investigate some properties of the class $BM(X_1,X_2,X_3)$ for general spaces which are invariant under translation, modulation and dilation, analyzing also the particular case of r.i. Banach function spaces. We shall give some examples in this class and some procedures to generate new bilinear multipliers. We shall focus in the case $m(\xi,\eta)=M(\xi-\eta)$ and find conditions for these classes to contain non zero multipliers in terms of the Boyd indices for the spaces.
Abstract:
The Vortex Filament Equation (VFE) is a model for the dynamics of a vortex _lament in a 3-D inviscid incompressible uid, and due to its geometric properties and simplicity, it has received a lot of attention recently. Given an arc-length parameterized curve X(s; _) in R3, the equation describes its evolution as
Where ^ is the usual cross product, s arc-length parameter, t time and subscripts denote the partial derivatives.
In this talk, we consider the initial datum X(s; 0) as a regular polygonal curve in the Euclidean geometry; through algebraic and numerical results, it will be shown that X(s; t) is a skew polygon at any rational time. Hence, we will see that the evolution can be related to the \Talbot e_ect" in optics. We also comment on the trajectory of one point, i.e., X(0; t) which appears to be a multifractal and resembles to the so-called Riemann's non-differentiable function.
Abstract:
This talk will provide an overview of some of the main ideas in the theory of spacings, i.e. the gaps between successive observations. After reviewing some basic properties of spacings, their use in testing statistical hypotheses and in estimating parameters will be discussed. Two-sample tests based on “spacings-frequencies” and their relationship to locally most powerful rank tests will be explored, as are some possible extensions to observations in higher dimensions.
Abstract:
This talk provides an easy introduction to the novel area of statistics, where the observations are “directions”. It is introduced by raising various scientific issues where the empirical evidence comes in the form of measuring directions, and how such measurements answer the question at hand. Such examples arise in many natural sciences like geology and biology where one may be directly measuring directions in two or three dimensions, as well as in several other seemingly unrelated and unexpected situations. New descriptive measures as well as statistical models are needed for studying such data, and the basic question one needs to answer before doing any inference in this context, is to ask if the data exhibit any preferred direction i.e. test for isotropy.
Abstract:
The theory of semihypergroups and hypergroups allows a detailed study of measure algebras that can be expressed in terms of a convolution of measures on the underlying spaces. In particular, the class of semihypergroups contains many important examples of coset and orbit spaces in locally compact groups, which do not have enough structure to be a semigroup or a hypergroup. The lack of an extensive prior research since its inception in 1972 and the signi_cant examples it contains in coset theory, orbit spaces and homogeneous spaces, opens up a number of intriguing new paths of research on semihypergroups.
In our talk, we will give a brief overview on how some well-known algebraic and analytic concepts and language of classical semigroup and group theory can be translated for semihypergroups, and investigate where the theory deviates from the classical theory of semigroups. In particular, we will discuss ideals and homomorphisms, spaces of almost periodic and weakly almost periodic functions and free-product structures in the category of semihypergroups.
Abstract:
This talk will provide a brief exposition to variable selection and sparse recovery using the L_1 penalty. Primarily, I will talk about the primal-dual witness approach and geometric insights into sparse recovery.
Abstract:
Prof. Chatterjee will discuss basic facts about high dimensional model selection in regression setup. It is currently a burning area of research in statistics. He will state and explain some recent non-asymptotic results.
Abstract:
Prof. Chatterjee will discuss basic facts about high dimensional model selection in regression setup. It is currently a burning area of research in statistics. He will state and explain some recent non-asymptotic results.
Abstract:
We consider the problem of analysis of variance, where the sample observations are random functions, and propose a test based on spatial signs. An asymptotic implementation and a bootstrap implementation of this test are developed, and their properties are investigated. We compare the performance of our test with that of several mean based tests of ANOVA for functional data in the literature, and found that Our test not only outperforms the mean based tests in several non-Gaussian models with heavy tails, but in some Gaussian models also, it exhibits better performance than the mean based tests.
Abstract:
In this talk I will give a brief introduction to G_2 geometry and gauge theory on G_2 manifolds. I will discuss the deformation theory of instantons on nearly G_2 manifolds. We will study the deformation space by identifying it as the kernel of a Dirac operator and will use this identification to specify some cases where the deformation space is trivial.
Abstract:
We shall discuss how one can estimate values of various Diophantine exponents for standard linear actions of some $2 \times 2$ matrix groups provided we have continued fraction algorithms whose denominator sizes rise exponentially. Thereafter, we illustrate this with few cases which we have been able to resolve satisfactorily. This builds upon previous works of Bugeaud, Dani, Laurent and Nogueira, among many others
The talk will be partly based on joint work with Yann Bugeaud and Zhenliang Zhang.
Abstract:
In this talk, I will first give some historical account of work on cure models. I will then describe some of the important cure rate models and then present a flexible cure rate model that encompasses some of the special cases and describe both direct maximum likelihood estimation and an efficient EM algorithm. I will then discuss some model discrimination results. Finally, I will describe some generalizations including proportional hazards model, proportional odds model, and some destructive cure models. All the models will be illustrated with some melanoma data sets.
Abstract:
A celebrated theorem of Margulis characterizes arithmetic lattices in terms of density of their commensurators. A question going back to Shalom asks the analogous question for thin subgroups. We shall report on work during the last decade or so and conclude with a recent development. In recent work with Thomas Koberda, we were able to show that for a large class of normal subgroups of rank one arithmetic lattices, the commensurator is discrete.
Abstract:
We study first passage percolation (FPP) in a Gromov-hyperbolic group G with boundary equipped with the Patterson-Sullivan measure. We associate an i.i.d. collection of random passage times to each edge of a Cayley graph of G, and investigate classical questions about asymptotics of first passage time as well as the geometry of geodesics in the FPP metric. Under suitable conditions on the passage time distribution, we show that the 'velocity' exists in almost every direction, and is almost surely constant by ergodicity of the G-action on the boundary.
For every point on the boundary, we also show almost sure coalescence of any two geodesic rays directed towards the point. Finally, we show that the variance of the first passage time grows linearly with word distance along word geodesic rays in every fixed boundary direction.
This is joint work with Riddhipratim Basu.
Abstract:
Abstract:
Warped cone is a geometric object associated with a measure preserving isometric action of a finitely generated group on a compact manifold. It encodes the geometry of the manifold, geometry of the group (Cayley graph) and the dynamics of the group. This geometric object has been introduced by J. Roe in the context of Coarse Baum-Connes conjecture (CBC conjecture). Warped cones associated with the action of amenable groups give examples of CBC conjecture and some expander graphs can be constructed from the warped cones associated with the action of Property (T) group. On the other hand, Measured Equivalence (ME) is an equivalence relation between two countable groups introduced by M. Gromov as a measure-theoretic analogue of quasi-isometry. If the ‘cocyles’ associated with a measured equivalence relation are bounded, the relation is called Uniform Measured Equivalence. In this lecture, we prove that if two warped cones are quasi-isometric, then the associated groups are Uniform Measured Equivalent. As an application, we will talk about different ME-invariants which distinguish two warped cones up to quasi-isometry. This is a work in progress.
Abstract:
I will give a brief introduction to A^1-homotopy theory and describe some applications to algebraic geometry. The presentation will be non-technical and will be based on a lot of examples.
Abstract:
Consider k ($\geq 2$) populations characterized by k probability distributions that differ only in the numerical value of a parameter (say mean). In the analysis of variance if the hypothesis of homogeneity of populations is rejected then a natural question to ask is that which of the k populations is the best population, where a population is considered to be better than the other if the numerical value of some function of the parameter associated with it is larger (or smaller) than the corresponding value for the other population. Ranking and selection problems provide a satisfactory solution to this problem. Although the ranking and selection problems have been extensively studied in the literature since 1950 there are still some unresolved problems in the area.
In this talk we will discuss one such unresolved problem and discuss a partial solution to this problem. For the ease of presentation, the problem will be discussed through the example of gamma populations.
Abstract:
The E_2-term of the Adams spectral sequence may be identified with certain derived functors, and this also holds for other Bousfield-Kan types spectral sequence.
In this talk, we'll explain how the higher terms of such spectral sequences are determined by truncations of relative derived functors, defined in terms of certain spectrally enriched functor called mapping algebras.
This is ongoing joint work with David Blanc.
Abstract:
Abstract:
Abstract:
Abstract:
Abstract:
In 1812, F. Gauss introduced classical hypergeometric series to the Royal Society of Sciences at Gotingen. Since then, this kind of special functions have been well studied by mathematicians and established many significant contributions in different branches of mathematics. In the meantime, based on an analogy between the character sum expansion of a complex valued function over finite field and the power series expansion of an analytic function, J. Greene developed an analogue for classical hypergeometric series over finite field. This function is known as Gaussian hypergeometric function. Gaussian hypergeometric functions were introduced to have a parallel study with classical hypergeometric series. However, Gaussian hypergeometric functions have certain limitations. To overcome the limitations, D. McCarthy introduced an analogue for classical hypergeometric series in the p-adic setting. In this talk, we will discuss Gauusian hypergeometric functions and hypergeometric functions in the p-adic setting. Hypergeometric functions have been applied to different areas of mathematics but the two areas of most interest to us are their relations with the traces of Hecke operators and Kloosterman sums. In the first part of the talk, we will discuss certain connections of hypergeometric functions with the traces of Hecke operators. In the 2nd part we will review Kloosterman sums and their relations with hypergeometric functions.
Abstract:
In a large variety of fluid systems, flow properties are a function of space and time, and their variation can have a dramatic effect on the flow instability. The knowledge of instability behaviour of such flow is essential for mathematical modeling, design and application of compact tools to ensure desired mechanical, optical properties and barriers of the products. Moreover, many intriguing and important fluid dynamic phenomena in nature and engineering tools are associated with complex spatio-temporal patterns (e.g. water waves, clouds, sprays, blood flow and turbulent flows in various industries etc.). The study of hydrodynamic stability is an easier way to understand the spatio-temporal behaviour of complex flow systems. This talk includes the discussion on modal linear stability analysis, analytical and numerical techniques for solving stratified multilayer problems. I will explain how the instability characteristics of bounded as well as semi-bounded viscosity-stratified flows alter effectively by scalar diffusion and boundary slip. I will also discuss the derivation of generalized Orr-Sommerfeld equation and Reynolds-Orr energy equation for stratified miscible flow with Navier-slip boundary condition.
Abstract:
We are often interested in problems in which we look for a solution y(x) of a differential equation so that y(x) satisfies a prescribed condition—that is, condition imposed on the unknown y(x) or its derivatives. In this talk, I want to discuss about the existence and uniqueness of solution for such kind of equation. I will define an initial value problem (IVP) and seek general existence theorem for real solution. I will also explain how a unique solution of the initial value problem, can be obtained by an approximation process and check the necessary/sufficient conditions for the unique solution.
Abstract:
In this talk I will give an exposition on two remarkable results of Sudipta (one jointly with P. Bandyopadhyay and the other with D. Narayana) on the geometry of subspace of finite co-dimension in space of continuous functions on a compact set K. These results which are nearly a decade old had a great impact on the study of the structure of such subspaces in other classes of Banach spaces.
Abstract:
No
Abstract:
The aim of this talk is to explain the behaviour of some conformal metrics and invariants near a smooth boundary point of a domain in the complex plane. We will be interested in the invariants associated to the Carathéodory metric such as its higher-order curvatures that were introduced by Burbea and the Hurwitz metric.
The basic technical step in all these is the method of scaling the domain near a smooth boundary point. To estimate the higher-order curvatures using scaling, we generalize an old theorem of Suita on the real analyticity of the Carathéodory metric on planar domains and in the process, we show convergence of the Szegő and Garabedian kernels as well.
We then talk about the Hurwitz metric that was introduced by D. Minda. Its construction is similar to the Kobayashi metric but the essential difference lies in the class of holomorphic maps that are considered in its definition. We show that this metric is continuous and also strengthen Minda’s theorem about its comparability with the quasi-hyperbolic metric by estimating the constants in a more natural manner.
Abstract:
In Langlands program certain invariant linear functionals on irreducible representations of algebraic groups over locally compact _elds (ex: GL2(R), GL2 (Qp)) play a central role. The simplest version of these linear functionals are called Whittaker functionals. Whittaker functionals are deeply related to invariant harmonic analysis on such groups, with arithmetic and geometry. For instance, for the group GL2, the existence of Whittaker linear functional imply the multiplicity one results in the theory of automorphic representations. The situation of multiplicity one fails for almost all other linear groups and this failure is captured by Langlands formalism of dual group. I will explain my results in the case of unitary groups in three variables.
Finally, if time permits, we shall see some weak estimates on the generalized upper and lower curvatures of the Hurwitz metric.
Abstract:
This is joint work with Marc Technau (University of Graz). We generalize a classical result by R.C. Vaughan on Diophantine approximation restricted to fractions with prime denominator to imaginary quadratic number field of class number one. Our treatment is based on Harman's sieve method in the number field setting. Moreover, we introduce a smoothing which allows us to make conveniently use of the Poisson summation formula.
Abstract:
A collective motion of cells which responds to an attractant gradient is known as “chemotaxis”. Chemotaxis-convection-diffusion is a particular type of bio convection. Due to its significant role in medical, industrial, and geophysical areas, research effort has been performed to understand the dynamics of the bacterial motility in suspension, studies through analytical, experimental, and numerical attempts previously were only for a flat free-surface of a suspension of chemotaxis bacteria in a shallow/deep chamber. We consider now a three-dimensional chemotaxis-convection-diffusion flow system with a deformed free surface. The influences of the aggregated chemotactic cells on the deformed free surface of a shallow chamber are studied analytically. The aim of our research work is to explore the nature of the instability in the system by performing a detailed linear stability analysis of steady-state oxygen and cell concentration distributions. A weakly nonlinear stability analysis has been carried out as well to determine the relative stability of the pattern formation at the onset of instability where Rayleigh number R_(α_T ) is the nonlinear control parameter of the system. The system becomes dominated by nonlinear convection terms beyond a critical R_(α_T ) , which also depends on the critical wavenumber k and Nusselt number N_(u_T ) as well as the other parameters. We have investigated the issue of how the critical R_(α_T ) in this system varies with three different sets of parameters. The Lorenz model is derived under the assumption of Bossinesq approximation. Using the method of multiscales, a Ginzburg-Landau equation is derived from the Lorenz model, the solution of which helps to quantify the energy transport through the Nusselt number N_(u_T )
Abstract:
In 1980s Goldman introduced various Lie algebra structures on the free vector space generated by the free homotopy classes of closed curves in any orientable surface F. Naturally the universal enveloping algebra and the symmetric algebra of these Lie algebras admit a Poisson algebra structure. In this talk I will define and discuss some properties of these Poisson algebras. I will explain their connections with symplectic structure of moduli space and the skein algebras of F\times [0,1] . I will also discuss how to compute center of these Poisson algebras using geometric group theory. I will mention some open problems related to these objects.
Abstract:
Differential equations have fundamental importance in engineering mathematics because many physical laws and relations can be expressed mathematically in the form of differential equations. The mathematical problems of science and engineering fields can appear as a differential equations. For example, the problem of satellite motion, current flow in an electric circuit, population growth, radioactive decay, temperature control etc. lead to differential equations. Each of the above problems are characterized by some laws which involve the rate of change of one or more quantities, with respect to the other quantities. The laws characterizing these problems when expressed mathematically, become equations involving derivatives and such equations are called differential equations. It is important to study the methods of ordinary differential equations to solve these problems. Differential equations that depends on a single variable is called as ordinary differential equations. Simplest method to be discussed are ODEs of the first order because they involve only the first derivative of the unknown function. Some first-order ODEs examples will be solved and plot their solution curve.
Abstract:
It is well known from a result of Milnor on the topology of isolated singularities that the Milnor number is a topological invariant in the complex case. We will show that the Milnor number in the real case is not a bi-Lipschitz invariant. We will produce a one-parameter deformation of a singularity which is bi-Lipschitz trivial but the Milnor number is different for two different values of the parameter variable.
Abstract:
Abstract:
Define a configuration in R^n to be a family C of finite subsets of the R^n which is closed under dilations. We say that X avoids C if no set in C is contained in X. We will discuss some problems of the following form: Given a configuration C in R^n and a subset X of R^n, can we find a "large" subset Y of X such that Y avoids C? "Y is a large subset of X" will be interpreted both measure theoretically (Y has the same Lebesgue outer measure as X) and topologically (Y is everywhere non meager in X).
Abstract:
An algorithm is a step by step procedure to solve a problem. Every algorithm has inherited parallelism in it. But all algorithms cannot be parallelized. To explore the inherited parallelism of an algorithm, few basic steps play a vital role. Interconnection network is one of such steps. Few algorithm’s performance is suited to a specific kind of interconnection network. The present talk will explore such interconnection networks and will also discuss about the problems which have better performance over which network.
Abstract:
In this talk, we discuss a semi-discrete finite difference scheme for a conservation laws driven by noise. Thanks to BV estimates, we show a compact sequence of approximate solutions, generated by the finite difference scheme, converges to the unique entropy solution of the underlying problem, as the spatial mesh size goes to zero. Moreover, we show that the expected value of the L^1 difference between the approximate solution and the unique entropy solution converges at an expected rate.
Abstract:
Several types of spatiotemporal patterns for ecological communities are ubiquitous in natural habitat such as the vegetation patterns in semiarid region and the patchy spatial distribution in plankton ecosystem. It has been believed that the generation of spatiotemporal pattern in ecological communities is a result of the combination effect of the local and external factors. There exist several external factors, such as chemical-physical limitations and environmental heterogeneity, which take part in shaping the dynamics of ecological communities. However, there exist numerous empirical evidences which suggest that one should not point at the environmental heterogeneity as sole reason behind the emergence of spatiotemporal patterns. On the other hand, studies indicate that internal factors can lead to spatiotemporal pattern formation in a completely homogeneous environment and this gives rise to the well-known theory of the self-organized pattern formation. The theoretical study on self-organized pattern formations in ecological communities has been accomplished by analyzing the reaction-diffusion systems which take into account the random movements of the concerned species. In this presentation, we will talk about a complete self-organized pattern formation scenario for a spatiotemporal prey-predator model with strong Allee effect in prey growth, Holling type-II functional response and density dependent death rate of predator. The effect of the half-saturation constant on the emergence of different types of stationary patterns and the persistence enhancing effect of the spatial component will be discussed. Also, we will present different types of invasive patterns and their implications on control and management strategies for invasive species. Further, we will discuss about the destabilizing effect of gestation delay on spatial distributions of the concerned species. Overall, a comparative study between the dynamics of spatial and corresponding non-spatial systems will be presented.1
Abstract:
Sign changes of Fourier coefficients of cusp forms are central problem in number theory and many results have been obtained in this direction. In particular, it is interesting to study the sign changes at subsequences. In this talk, we will consider the problem of sign changes of Fourier coefficients of cusp form at sum of two squares and will give a quantitative result in this direction.
Abstract:
In this talk we will describe the Safety Analysis of the Indian Oceanic Airspace project, which Indian Statistical Institute is conducting jointly with the Airports Authority of India (AAI), starting from the year 2011. The talk will concentrate on the understanding of the goal of the project, typical data structure and the current "state of the art". We will also discuss some of the statistical challenges related to such an analysis.
Abstract:
The Selmer group of an elliptic curve over a number field encodes several arithmetic data of the curve providing a p-adic approach to the Birch and Swinnerton Dyer, connecting it with the p-adic Lfunction via the Iwasawa main conjecture. Under suitable extensions of the number field, the dual Selmer becomes a module over the Iwasawa algebra of a certain compact p-adic Lie group over Z_p (the ring of padic integers), which is nothing but a completed group algebra. The structure theorem of GL(2) Iwasawa theory by Coates, Schneider and Sujatha (C-S-S) then connects the dual Selmer with the “reflexive ideals” in the Iwasawa algebra. We will give an explicit ring-theoretic presentation, by generators and relations, of such Iwasawa algebras and sketch its implications to the structure theorem of C-S-S. Furthermore, such an explicit presentation of Iwasawa algebras can be obtained for a much wider class of p-adic Lie groups viz. pro- p uniform groups and the pro-pIwahori of GL(n,Z_p). If we have time, alongside Iwasawa theoretic results, we will state results (joint with Christophe Cornut) constructing Galois representations with big image in reductive groups and thus prove the Inverse Galois problem for p-adic Lie extensions using the notion of “p-rational” number fields.
Abstract:
When examining dependence in spatial data, it can be helpful to formally assess spatial covariance structures that may not be parametrically specified or fully model-based. That is, one may wish to test for general features regarding spatial covariance without presupposing any particular, or potentially restrictive, assumptions about the joint data distribution. Current methods for testing spatial covariance are often intended for specialized inference scenarios, usually with spatial lattice data. We propose instead a general method for estimation and testing of spatial covariance structure, which is valid for a variety of inference problems (including nonparametric hypotheses) and applies to a large class of spatial sampling designs with irregular data locations. In this setting, spatial statistics have limiting distributions with complex standard errors depending on the intensity of spatial sampling, the distribution of sampling locations, and the process dependence. The proposed method has the advantage of providing valid inference in the frequency domain without estimation of such standard errors, which are often intractable, and without particular distributional assumptions about the data (e.g., Gaussianity). To illustrate, we develop the method for formally testing isotropy and separability in spatial covariance and consider confidence regions for spatial parameters in variogram model fitting. A broad result is also presented to justify the method for application to other potential problems and general scenarios with testing spatial covariance. The approach uses spatial test statistics, based on an extended version of empirical likelihood, having simple chi-square limits for calibrating tests. We demonstrate the proposed method through several numerical studies.
Abstract:
We will begin with a quick review of quantum channels and briefly present the celebrated Choi-Kraus representation theorem. These constitute the key concepts and results that are required to move forward and define a special class of quantum channels called "entanglement breaking channels" --- the quantum channels that admit a Choi-Kraus representation consisting of rank-one Choi-Kraus operators.
We then introduce the entanglement breaking rank of an entanglement breaking channel and define it to be the least number of rank-one Choi-Kraus operators required in its Choi-Kraus representation. We shall show how this rank parameter for a certain map links to an open problem in linear algebra: Zauner's conjecture. In particular, we show that the problem of computing the entanglement breaking rank of the quantum channel, that sends X in M_d to 1/(d+1) [X + Tr(X)I_d] in M_d, is equivalent to the existence problem of SIC POVM in dimension d. This is a joint work with Vern Paulsen, Jitendra Prakash, and Mizanur Rahman.
Abstract:
In this talk, we will discuss the problem whether two regression functions modelling the relation between a response and covariate in two samples differ by a shift in the horizontal and vertical axis. We consider a nonparametric situation assuming only smoothness for the regression functions. A graphical tool based on the derivatives of the regression functions and their inverses is proposed to answer this question and studied in several examples. We also formalize this question in a corresponding hypothesis and develop a statistical test. The asymptotic properties of the corresponding test statistic are investigated under the null hypothesis and under local alternatives and the finite sample properties of the new test are investigated by means of a small simulation study and real data example. This is a joint work with Holger Dette (University of Ruhr, Germany) and Weichi Wu (Tsinghua University, China).
Abstract:
In this talk, we will discuss estimation and prediction inferences for the generalized half normal and Kumaraswamy distributions under different censoring schemes. In particular we will discuss hybrid Type-I censoring, Type II progressive hybrid censoring and adaptive Type-II progressive censoring schemes. Likelihood inference and Bayesian inference will be addressed under different censoring schemes. Further we will discuss about prediction estimates and associated intervals of censored/ future observations using both frequentist and Bayesian approaches. We will numerically compare different estimations and prediction estimates. We will illustrate different methods using various real data sets. Finally we will discuss some ongoing research problem on step stress life testing model.
Abstract:
Lang, Jorgenson, and Kramer have successfully employed techniques coming from theory of heat kernel, to study and estimate various arithmetic invariants. Inspired by their ideas, we describe an approach to study estimates of cusp forms, using theory of heat kernels.
Abstract:
Let G be a connected reductive group over a finite field f of order q. When q is small, we make further assumptions on G. Then we determine precisely when G(f) admits irreducible, cuspidal representations that are self- dual, of Deligne-Lusztig type, or both. Finally, we outline some consequences for the existence of self-dual supercuspidal representations of reductive p-adic groups. This is a joint work with Jeffrey Adler.
Abstract:
Given a smooth function f : [0,1) --> \R, and scalars u_j, v_j in (0,1), I will compute the Taylor (Maclaurin) series of the function F(t) := \det A(t), where A(t) is the 2x2 matrix
f( t u_1 v_1 ) f( t u_1 v_2 )
f( t u_2 v_1 ) f( t u_2 v_2 )
C. Loewner computed the first two of these Maclaurin coefficients, in the thesis of his student R.A. Horn (Trans. AMS 1969). This was in connection with entrywise functions preserving positivity on matrices of a fixed dimension -- the case of all dimensions following from earlier work of Schur (Crelle 1911) and his student Schoenberg (Duke 1942).
It turns out that an "algebraic" family of symmetric functions is hiding inside this "analysis". We will see how this family emerges when one computes the second-order (and each subsequent higher-order) Maclaurin coefficient above. This family of functions was introduced by Cauchy (1800s) and studied by Schur in his thesis (1901). As an application, I will generalize a determinant formula named after Cauchy to arbitrary power series (over any c ommutative ring); the above is the special case f(x) = 1/(1-x) and t=1.
Abstract:
I want to explain the oldest unsolved major problem in Mathematics (called the congruent number problem). It can be traced back at least to the 10th century but it is possibly much older. It turns out to be a beautiful example of the modern theory of the arithmetic of elliptic curves, but it is more accurate to say that this theory grew out of the study of this problem.
In the 17th century, Fermat gave a wonderful proof of the first special case of this problem. It also led Fermat to his so called Last Theorem (now solved by Andrew Wiles). But the original congruent number problem remains unsolved, despite the fact that conjecturally there is a very simple and beautiful answer to it.
Abstract:
Over the last few decades, models based on fluid flow and deformation in porous media are getting a lot of attention because these models have wide range of applications in science and engineering. Specifically, Biot’s consolidation model has many applications which cover the range from geoscience to medicine. It is the aim of this talk to present the a posteriori error analysis for locking free mixed finite element method of Biot's consolidation model. We discuss three novel a posteriori error estimators and show that all three a posteriori error estimators are reliable, efficient and robust. Finally, numerical results are presented to validate the theoretical results.
Abstract:
Estimation of animal abundance and distribution over large regions remains a central challenge in statistical ecology. In our first study, we use a Bayesian smoothing technique based on a conditionally autoregressive (CAR) prior distribution and Bayesian regression to integrate data from reliable but expensive surveys conducted at smaller scales with cost-effective but less reliable data generated from surveys at wider scales to address this problem. We also investigate whether the random effects which represent the spatial association due to the CAR structure have any confounding effect on the fixed effects of the regression coefficients. Next, we develop a novel Bayesian spatially explicit capture-recapture (SECR) model that disentangles the latent ecological process of animal arrival within a detection region from the process of recording this arrival by a given set of detectors. We integrate this into an advanced version of a recent SECR model by Royle (2015) involving partially identified individuals.
The above is a joint work with Prof. Mohan Delampady.
Abstract:
This is an informal talk meant for aspiring researchers in Mathematics and related fields such as Theoretical Physics. The purpose of this talk is to convey a sense of what it takes, on a day to day basis, to succeed in research. I would like to lay bare the inner attitude of a researcher. It is based partly on my own experience, but mostly on what I have learnt while collaborating, and generally hobnobbing, with some truly great mathematicians of our times. The talk will be totally non-technical and I hope to make it very interactive.
Abstract:
The representation theory of string algebras started with the work of Gelfand and Ponomarev on Harish-Chandra representations of the Lorentz group. The methods they introduced were adapted and extended to cover the representation theory of a broad class of algebras. The term "string" algebra refers to the combinatorial description of their indecomposable finitely generated representions.
I will recall that description, and that of the morphisms between representations, outline the broad picture of the category of finitely generated modules in terms of Auslander-Reiten components and say something about the infinite-dimensional representation theory.
Abstract:
When _lms thin the viscous resistance of the con_ning surfaces controls key aspects of their dynamics. However, those surfaces do more than provide the typical boundary conditions. For example, if one of the boundaries is elastic, there are nonlocal interactions that lead to interesting and challenging mathematical problems and important applications. One unique setting occurs when the free surfaces of most solids approach the bulk melting temperature from below, and they are wet by the melt phase. Mathematically, the uid dynamics of this so-called \premelting" falls under the rubric of a class of higher-order di_usion equations governing the dynamics of viscous current down an incline, viscous gravity currents between a rigid surface and a deformable elastic sheet, wetting/dewetting, and a spate of other thin-_lm settings, to name a few. However, theunderlying forces driving the ow are uniquely associated with intermolecular forces. We discuss aclass of experimentally tested and testable premelting dynamics ows. Finally, through its inuence on the viscosity, the con_nemente_ect implicitly introduces a new universal length scale into the volume ux. Thus, there are a host of thin _lm problems, from droplet breakup to wetting/dewetting dynamics, whose properties (similarity solutions, regularization, and compact support) will changeunder the action of the con_nemente_ect. Therefore, our study suggests revisiting the mathematical structure and experimental implications of a wide range of problems within the framework of the con_nemente_ect."The game of Hex gives a constructive proof of the Brouwer's fixed point theorem”
on Feb 21, 2019 at 4:00 PM in FB 567, MATHS Dept. Seminar room
by Prof. TES Raghavanfrom University of Illinois at Chicago

Abstract:
Abstract:
Abstract:
We will discuss results concerning conjugacy-invariant norms on free groups, in particular ones that
are homogeneous and quasi-homogeneous.On values of the Riemann zeta function at odd positive integers. on January 25, 2019 at 2:30 PM in FB 567, MATHS Dept Seminar room
by Prof. Atul Dixit from Gandhinagar
Abstract:
KMS states are generalization of what is known as Gibbs state for matrices to in_nitedimen-sional
C∗-algebras. Given an inverse temperature, unlike the Gibbs state for matrix algebra,KMS states
for general in_nite dimensional C∗algebras are far from unique. We discuss how theclassical and quantum symmetry of graphs act as symmetry objects for the corresponding graphC∗algebras and the invariance of KMS states on graph C∗algebras under such symmetries. Inparticular, we shall give an example of a graph admitting in_nitely many KMS states at criticalinverse temperature all of which are invariant under classical symmetry. But interestingly, thatgraph admits unique quantum symmetry invariant KMS state.
Absract:
A topological dynamical system is a pair (X,T) where T is a homeomorphism of a compact space X. A measure preserving action is a triple (Y, \mu, S) where Y is a standard Borel space, \mu is a probability measure on X and S is a measurable automorphism of Y which preserves the measure \mu. We say that (X,T) is universal if it can embed any measure preserving action (under some suitable restrictions).
Krieger’s generator theorem shows that if X is A^Z (bi-infinite sequences in elements of A) and T is the transformation on X which shifts its elements one unit to the left then (X,T) is universal. Along with Tom Meyerovitch, we establish very general conditions under which Z^d (where now we have dcommuting transformations on X)-dynamical systems are universal.
These conditions are general enough to prove that
1) A self-homeomorphism with non-uniform specification on a compact metric space (answering a question by Quas and Soo and recovering recent results by David Burguet)
2) A generic (in the sense of dense G_\delta) self-homeomorphism of the 2-torus preserving Lebesgue measure (extending result by Lind and Thouvenot to infinite entropy)
3) Proper colourings of the Z^d lattice with more than two colours and the domino tilings of the Z^2 lattice (answering a question by Şahin and Robinson) are universal. Our results also extend to the almost Borel category giving partial answers to some questions by Gao and Jackson.
The talk will not assume background in ergodic theory and dynamical systems.
Abstract:
The standard isoperimetric inequality states that among all sets with a given fixed
volume(or area in dimension 2) the ball has the smallest perimeter. That is, written here in dimension
2, the following infimum is attained by the ball
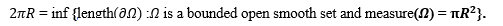
I will give an elementary overview on this inequality, such as techniques developed for theproof (symmetrization, variational method, Fourier series method in 2 dimensions), higherdimensional version, connections to partial differential equations and some generalizations. Iwill keep the talk basic, requiring no specialized knowledge in differential geometry and partial differential equations.
Abstract:
The dynamical setting of a non-autonomous system is related to the Bedford conjecture. Further,Short C^k's arises as basins of attraction of a fixed point in the non-autonomous setting. In this talk, I will discuss the relation between non-autonomous holomorphic dynamics, Short C^k's and their importance in the context of the Levi-problem. Also, I will give some construction of Short C^k's with pathological properties and finally discuss some related results and questions.
Abstract:
In multivariate linear regression, one of the major challenges is to model dependent responses from correlated predictors in a compact and interpretable manner. One promising approach is to model the coefficient matrix as a jointly sparse and low-rank matrix. Learning such a decomposition is, however, very challenging due to the simultaneous presence of orthogonality and sparsity constraints.Here, we introduce a divide and conquer strategy to infer such a coefficient matrix from data. In the divide step, we decompose the coefficient matrix into a sum of unit-rank matrices whose left and right singular vectors are sparse. In the conquer step, each unit-rank matrix is estimated either by a sequential(greedy) approach or an exclusive extraction approach. We show that the proposed algorithm is guaranteed to converge to an accumulation point and provide an efficient implementation in the R package secure. We demonstrate the efficacy of the procedure in simulation studies and two applications in genetics.
Abstract:
Over the last few decades, models based on fluid flow and deformation in porous media are getting a lot of attention because these models have wide range of applications in science and engineering. Specifically, Biot’s consolidation model has many applications which cover the range from geoscience to medicine. It is the aim of this talk to present the a posteriori error analysis for locking free mixed finite element method of Biot's consolidation model. We discuss three novel a posteriori error estimators and show that all three a posteriori error estimators are reliable, efficient and robust. Finally, numerical results are presented to validate the theoretical results.
Abstract:
The problem of estimating quantiles has received considerable attention by several researchers in the recent past from classical as well as decision theoretic point of view. It is noted that, exponential quantiles are widely used in the study of reliability, life testing and survival analysis, and related fields. Suppose there are k(≥2) normal populations with a common mean and possibly different variances. The problem of estimation of quantiles of the first population is considered with respect to a quadratic loss function. The concept of invariance is introduced to the problem. As a result, sufficient conditions are derived to improve affine and location equivariant estimators. Consequently, some complete class results have been obtained. Next, the problem of estimating ordered quantiles of two exponential distributions has been considered assuming equality on location parameters. Using order restriction on the quantiles, several new estimators have been proposed including the restricted maximum likelihood estimator. Using quadratic loss function, a sufficient condition has been obtained to improveequivariant estimators under the order restriction. Consequently, some improved estimators have been obtained. All the proposed estimators have been compared numerically. It has been seen that the percentage of risk reduction after using order restriction is quite significant.
Lack-of-fit of a parametric AR(1) model in the presence of measurement error.On January 14, 2019 at 11:00 AM in FB567, MATHS Dept Seminar room
by Prof. Hira Koul from Department of Statistics & Probability, Michigan State University
Abstract:
Recently, power law (also known as Zipf's law) has been turned out to be very natural in modelling and inferring about networks, finance, environment studies, rare events. In this seminar, Hill's estimator (best known to estimate index of regular variation) will be discussed with examples. We shall talk about the advantages and disadvantages of using Hill's estimator once population deviates from pure power law. We shall also raise some issues which are yet to be resolved.
Abstract:
We consider the limiting behaviour of the point processes associated with a branching random walk with supercritical branching mechanism and balanced regularly varying step size. Assuming that the underlying branching process satisfies Kesten-Stigum condition, it is shown that the point process sequence of properly scaled displacements coming from the n-th generation converges weakly to a Cox cluster process. This is a joint work with Rajat Subhra Hazra and Parthanil Roy.
Abstract:
We will start by defining a G_2 and a nearly G_2 structure on a seven dimensional manifold M. After surveying known results about G_2 manifolds and explaining the importance of such manifolds, we will talk about hypersurfaces of a G_2 manifold, which inherits an SU(3) structure from the ambient G_2 structure. We will give a necessary and sufficient condition for a hypersurface of a nearly G_2 manifold to be nearly Kahler.
After that, we will focus our attention on minimal hypersurfaces (zero mean curvature) and will discuss some new results in that direction.
Abstract:
Sequential multiple assignment randomized trials (SMART) are used to construct data-driven optimal treatment strategies for patients based on their treatment and covariate histories in di_erent branches of medical and behavioral sciences where a sequence of treatments are given to the patients; such sequential treatment strategies are often called dynamic treatment regimes (DTR). In the existing literature, the ma- jority of the analysis methodologies for SMART studies assume a continuous primary outcome. However, ordinal outcomes are also quite common in clinical practice; for example, the quality of life is often measured in an ordinal scale (e.g., poor, moderate, good). In this work, _rst, we develop the notion of dynamic generalized odds-ratio (dGOR) to compare two dynamic treatment regimes embedded in a 2-stage SMART with an ordinal outcome. We propose a likelihood-based approach to estimate dGOR from SMART data. Next, we discuss some combinatorial properties of dGOR and derive the asymptotic properties of its estimate. We discuss some alternative ways to estimate dGOR using concordant-discordant pairs and multi-sample U-statistic. Then, we extend the proposed methodology to a K-stage SMART. Furthermore, we propose a basic policy search algorithm that uses dGOR to _nd an optimal DTR within a _nite class. A simulation study shows the performance of the estimated dGOR in terms of the estimated power corresponding to the derived sample size. We analyze data from Sequenced Treatment Alternatives to Relieve Depression (STAR*D), a multi-stage randomized clinical trial for treating major depression, to illustrate the proposed methodology. A freely available online tool using R statistical software is provided to make the proposed methodology accessible to other researchers and practitioners.
Abstract:
Quantile regression is a more robust, comprehensive, and flexible method of statistical analysis than the commonly used mean regression methods. Quantile function completely characterizes a distribution. More and more data is getting generated in the form of multivariate, functional, and multivariate functional data and the quantile analysis gets more challenging as the data complexity increases. We propose a set of quantile analysis methods for multivariate data and multivariate functional data. In plant science, the study of salinity tolerance is crucial to improving plant growth and productivity and we apply our methods to barley field data for a salinity tolerance analysis. We apply our methods to radiosonde wind data to illustrate our proposed quantile analysis methods for visualization, outlier detection, and prediction. We model multivariate functional data for flexible quantile contour estimation and prediction.
The estimated contours are flexible in the sense that they can characterize non-Gaussian and non-convex marginal distributions. We aim to perform spatial prediction for non-Gaussian processes.
Abstract:

Abstract:
Arens irregularity of a Banach algebra is due to elements in its Banach dual which are not weakly almost periodic. The usual algebras in harmonic analysis (such as the group algebra or the Fourier algebra, when known) turned out to be all Arens irregular (even in an extreme way, as we shall see in the talk). To start, more than sixty years ago, Richard Arens himself proved that I_1 is irregular, and was followed by Mahlon Day proving the same result for many discrete groups including the abelian ones. A long exciting story followed after. The talk is an attempt to tell you the story and to explain the combinatorial reason (on the group or its dual) creating such irregularity.
Abstract:
These will be an informal talk on the use of Carleman estimates for formally determined inverse problems for hyperbolic PDEs.
Abstract: In this talk, we will discuss the existence theory of distributional solutions solving.

On a bounded domain Ω. The nonlinear structure A(x, t, Δu) is modelled after the standard parabolic p-Laplace operator. In order to do this, we develop suitable techniques to obtain a prior estimates between the solution and the boundary data. As a consequence of these estimates, a suitable compactness argument can be developed to obtain the existence result. An interesting ingredient in the proof is the careful use of the boundedness of a new type of Maximal function defined on negative Sobolev spaces. The a priori estimates proved discussed in this talk are new even for the heat equation on bounded domains.
